Слайд 2
Аналіз часового ряду (time series)
Нагадаємо приклади часових рядів
з попередньої лекції:
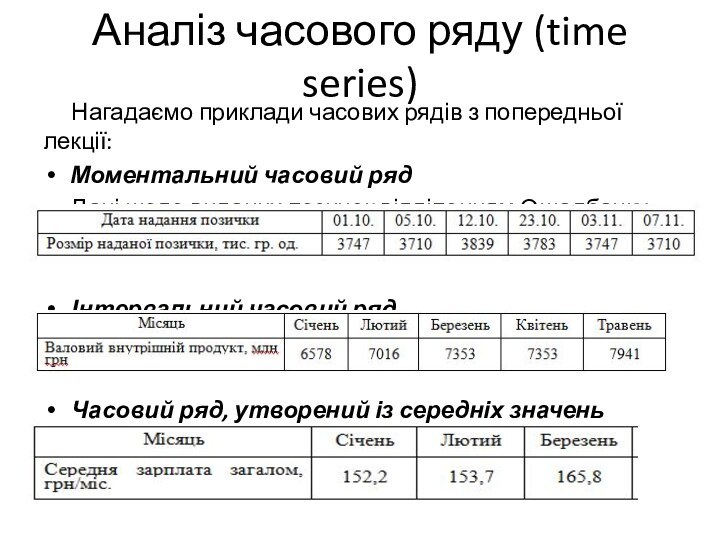
Моментальний часовий ряд
Дані щодо виданих позичок
відділенням Ощадбанку
Інтервальний часовий ряд
Часовий ряд, утворений із середніх значень показника
Слайд 3
Аналіз часового ряду (time series)
Умови коректності застосування математичного
апарату для аналізу часових рядів:
- порівнянність;
- однорідність;
- сталість;
- достатня
сукупність спостережень (репрезентативність).
Слайд 4
Аналіз часового ряду (time series)
Мета: побудова математичної моделі
ряду, за допомогою якої можна пояснити поведінку ряду і
здійснити прогноз на майбутні періоди.
Основні задачі дослідження часових рядів:
Статистичний аналіз (визначення природи й закону розподілу ряду, вивчення статистичних параметрів ЧР);
Прогнозування на підставі адекватних моделей.
Природа ряду:
1. Стаціонарні (білий шум, випадкове блукання, марківський процес)
2. Нестаціонарні (типів TS і DS; тренд-сезонні; нелінійні)
Слайд 5
Аналіз часового ряду (time series)
Мета: побудова математичної моделі
ряду, за допомогою якої можна пояснити поведінку ряду і
здійснити прогноз на майбутні періоди.
Основні етапи:
Побудова і вивчення графіка часового ряду стосовно наявності тренду, сезонності, циклічності та аномальних даних;
Визначення основних числових характеристик – описової статистики (середнє, медіана, дисперсія, стандартне відхилення, коефіцієнти асиметрії й ексцесу);
побудова гістограми для перевірки динамічного ряду на відповідність закону нормального розподілу;
Слайд 6
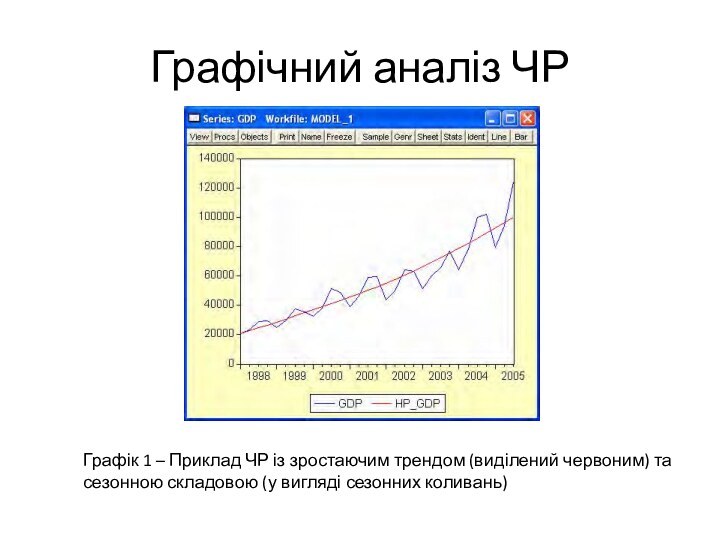
Графічний аналіз ЧР
Графік 1 – Приклад ЧР із
зростаючим трендом (виділений червоним) та сезонною складовою (у вигляді
сезонних коливань)
Слайд 8
Виявлення циклічних (регулярних) коливань
Для пошуку циклічних закономірностей у
динаміці певних показників використовується спектральний аналіз (аналіз Фур’є, перетворення
Фур’є, гармонійний аналіз; Spectral (Fourier) analysis), що передбачає перетворення динамічного ряду на послідовність синусоїдальних і косинусоїдальних функцій різних частот.
Основними характеристиками при спектральному аналізі є частота (f, довжина хвилі функції, що виражається кількістю циклів за одиницю часу) та період (T=1/f, тривалість одного повного циклу).
Слайд 9
Методи згладжування часового ряду
5. Мультиплікативна модель Холта-Вінтерса
Дана модель
використовує індекс сезонності:
Слайд 10
Виявлення аномальних рівнів
(при нормальному розподілі даних) метод
Ірвіна (модифікований)
ґрунтується на порівнянні сусідніх значень ряду
Послідовний розрахунок
за трьома спостереженнями величин:
Слайд 11
Метод Ірвіна (продовження)
2. Обчислити величину:
t = 2,
3,…, n.
3. Розраховані ковзні значення λt порівнюють із критичним
значенням λ для n=3 (λ3=2,3).
Якщо вони не перевищують критичне, то відповідні рівні вважаються нормальними.
Слайд 12
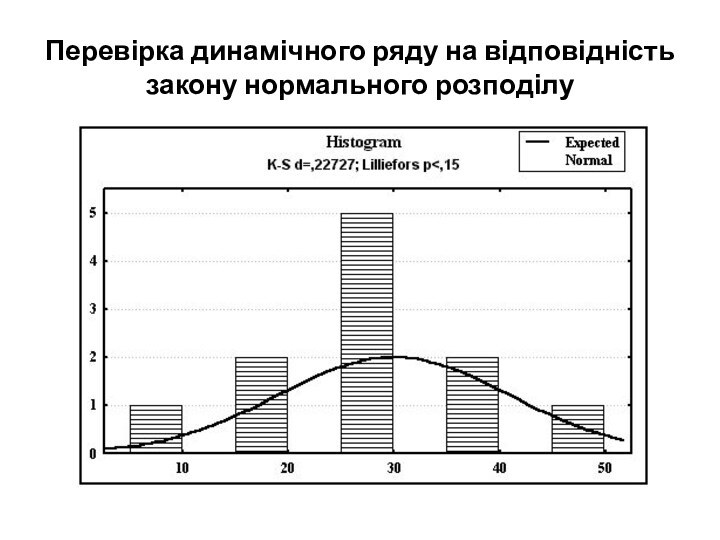
Перевірка динамічного ряду на відповідність закону нормального розподілу
Точна форма нормального розподілу – “дзвоноподібна крива” – визначається
лише двома параметрами: середнім і стандартним відхиленням. Для нормального розподілу характерним є те, що 68% всіх значень знаходяться в межах ±1 стандартне відхилення (standard deviation) від середнього, а діапазон ±2 стандартних відхилення включає 95% значень. Про відхилення від нормального розподілу свідчать коефіцієнти асиметрії (skewness) та ексцесу (kurtosis).
Слайд 13
Перевірка динамічного ряду на відповідність закону нормального розподілу
Найпростішим
способом перевірки динамічного ряду на відповідність нормальному розподілу є
побудова гістограми (histograms) – діаграми, яка показує, скільки значень попадає в кожний з інтервалів, на які можна розбити весь діапазон зміни певного показника, тобто частоту розподілу значень по інтервалах. На гістограму зазвичай накладається крива нормального розподілу, що дозволяє “на око” оцінити різні характеристики емпіричного розподілу.
Слайд 14
Перевірка динамічного ряду на відповідність закону нормального розподілу
Слайд 15
Перевірка динамічного ряду на відповідність закону нормального розподілу
Точнішу
інформацію про відповідність динамічного ряду нормальному розподілу можна отримати
за допомогою критеріїв нормальності, наприклад, критерію Пірсона ( ), критерію Колмогорова-Смірнова (K-S test for normality) чи критерію Ліллефорса (Lilliefors test for normality).
Слайд 16
Обрахунок стандартних статистичних параметрів, що характеризують динамічний ряд
Для стаціонарних динамічних рядів обраховуються стандартне відхилення (standard
deviation, застаріла назва – середньоквадратичне відхилення) та стандартна помилка (standard error). Стандартне відхилення розраховується за формулою:
де σ2 – дисперсія, SS – сума квадратів (sum of squares), n – величина динамічного ряду.
Стандартна помилка розраховується за формулою:
Слайд 17
Обрахунок стандартних статистичних параметрів, що характеризують динамічний ряд
Для
нестаціонарних динамічних рядів основним статистичним параметром є відхилення реальних
значень від тренду – середньоквадратична помилка (інколи – стандартне відхилення), що розраховується за формулою:
де yt – реальні значення, ŷt – трендові значення, n – кількість неспівпадінь реальних значень із трендовими
Слайд 18
Етапи аналізу ЧР на стаціонарність
(3) Перевірка часового ряду
на стаціонарність:
3.1. Побудова автокореляційної (корелограми) і часткової автокореляційної функції
для рівнів часових рядів, їх перших та других різниць.
3.2. Тест на наявність одиничних корнів – розширений тест Дікі-Фуллєра (augmented Dickey – Fuller test, ADF, або unit root test).
(4) Приведення до стаціонарного виду шляхом:
4.1. Виділення тренда – логарифмування – позначається літерою l ; знаходження перших або других різниць ряду – позначається літерою d (“difference”);
4.2. Сезонного згладжування –sa (“seasonal ajustment”);
4.3. Усунення аномальних значень, нормалізація ряду.
Слайд 19
Дослідження стаціонарності часового ряду в EViews
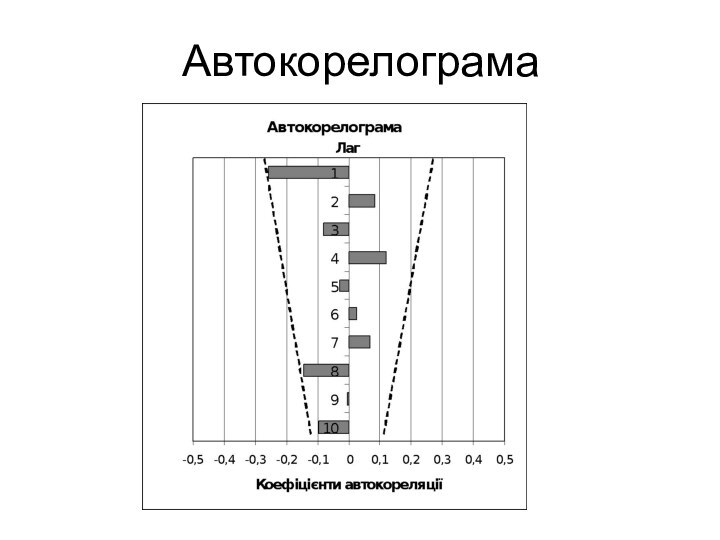
3.1. Побудова автокореляційної
(корелограми) і часткової автокореляційної функції з різними часовими лагами
для рівнів часових рядів, їх перших та других різниць .
Автокореляційна функція показує ступінь тісноти зв’язку між t спостереженнями часового ряду. Часткова автокореляційна функція розраховується за формулою часткового коефіцієнту кореляції. Корелограма і графік часткової автокореляційної функції мають швидко спадати зі зростанням t у разі стаціонарного ряду. Перевірка гіпотези про те, що автокореляція відсутня до k-го лагу включно, здійснюється за допомогою статистики Люнга-Бокса та її р-значення.
Слайд 21
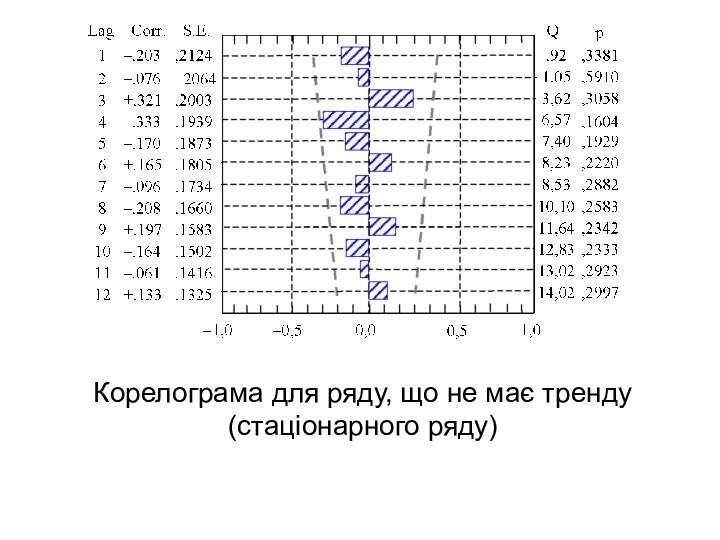
Корелограма для ряду, що не має тренду (стаціонарного
ряду)
Слайд 22
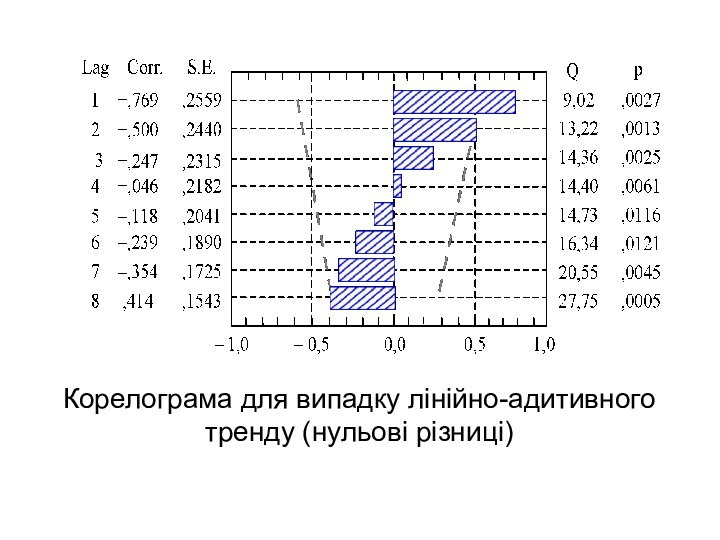
Корелограма для випадку лінійно-адитивного тренду (нульові різниці)
Слайд 23
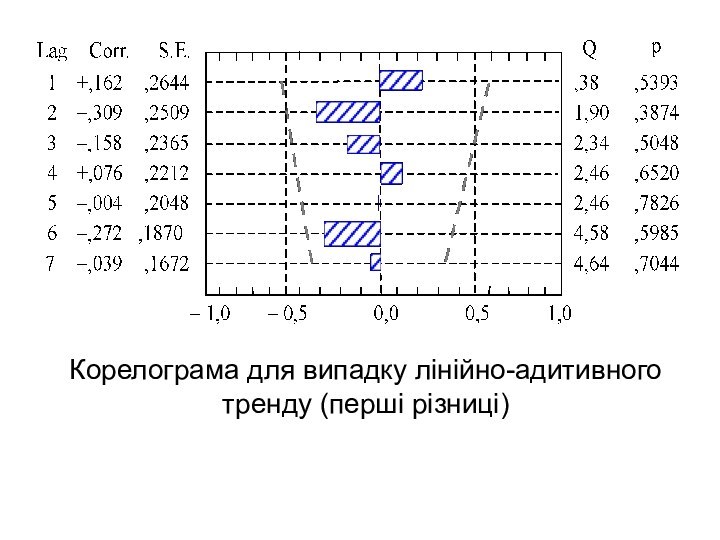
Корелограма для випадку лінійно-адитивного тренду (перші різниці)
Слайд 24
Корелограма ряду із сезонним коливанням (нульові різниці)
Слайд 25
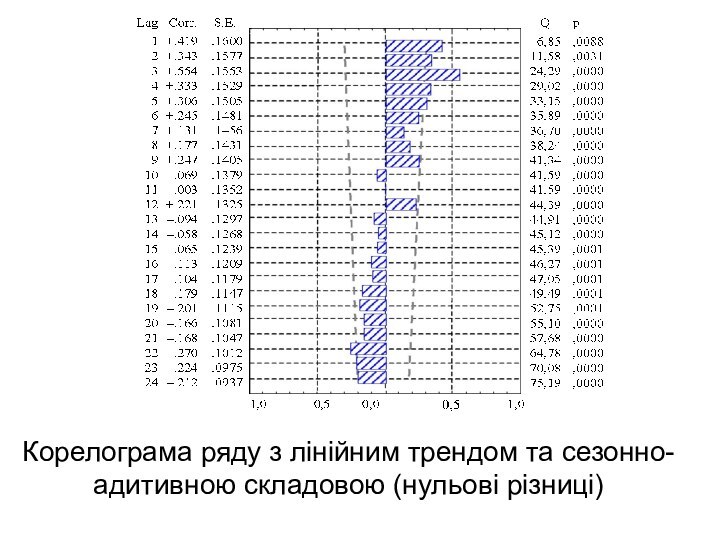
Корелограма ряду з лінійним трендом та сезонно-адитивною складовою
(нульові різниці)
Слайд 26
Корелограма ряду з лінійним трендом та сезонно-адитивною складовою
(перші різниці)
Слайд 27
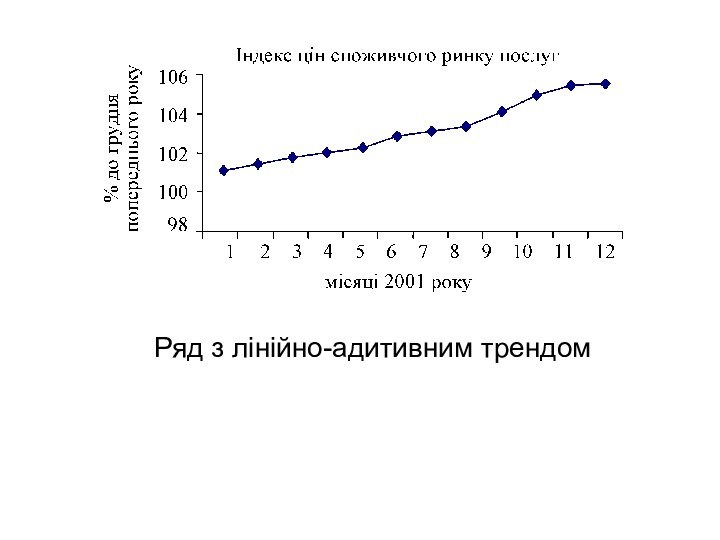
Ряд з лінійно-адитивним трендом
Слайд 29
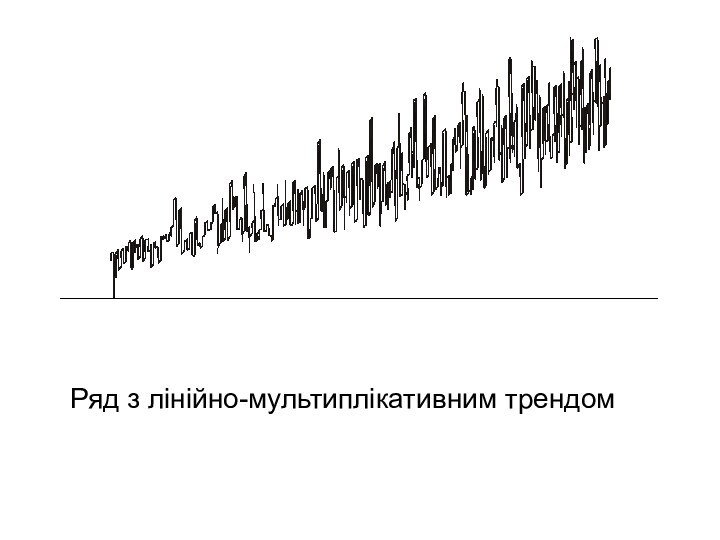
Ряд з лінійно-мультиплікативним трендом
Слайд 30
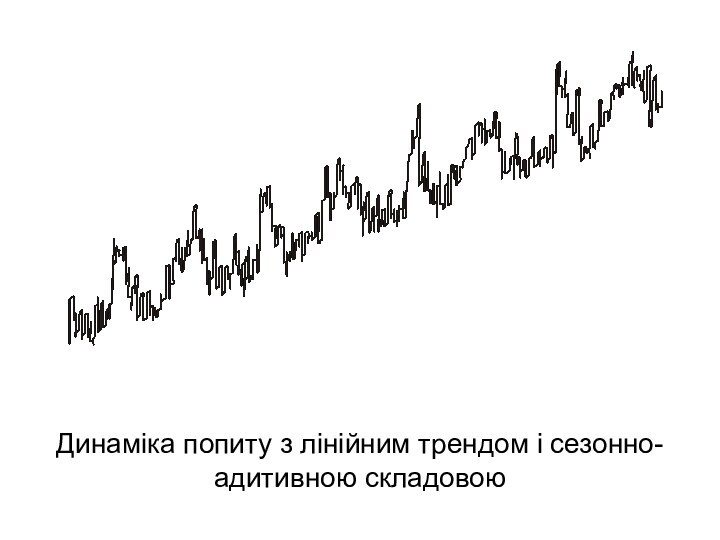
Динаміка попиту з лінійним трендом і сезонно-адитивною складовою
Слайд 31
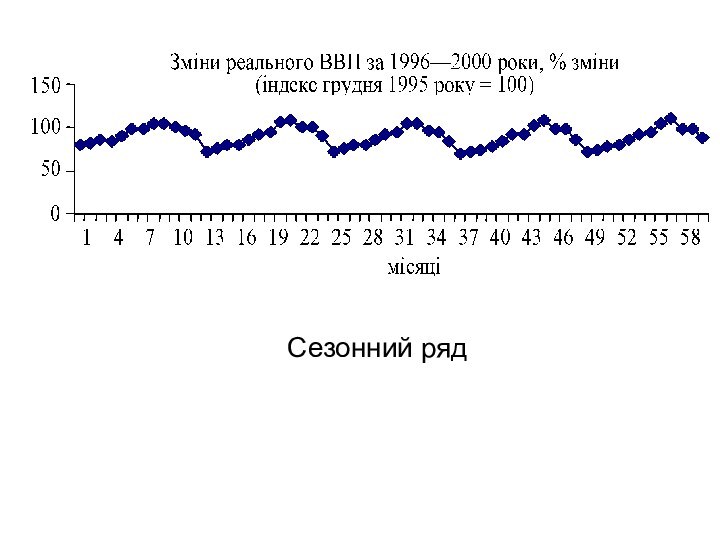
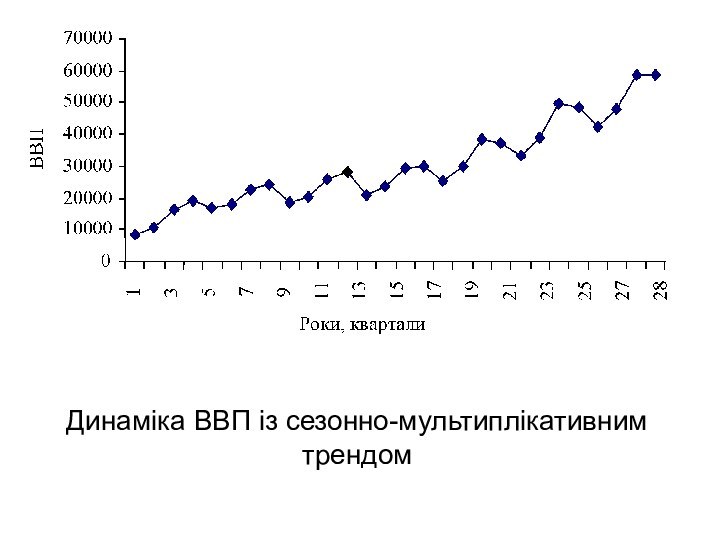
Динаміка ВВП із сезонно-мультиплікативним трендом