- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Логарифмическая функция
Содержание
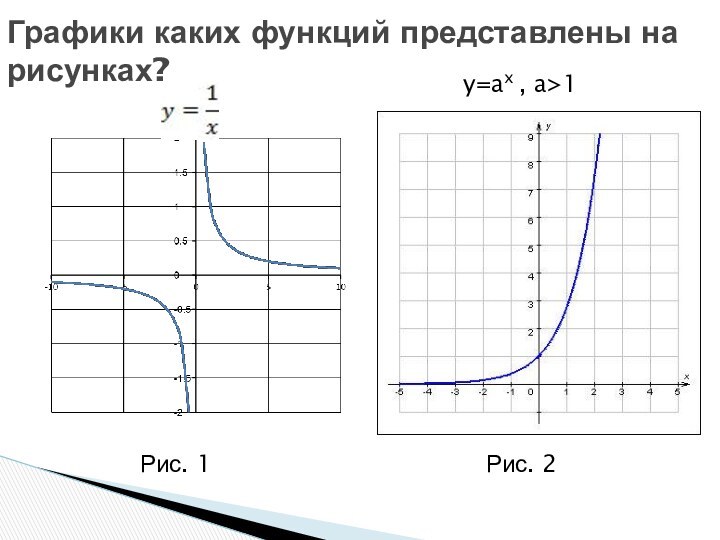
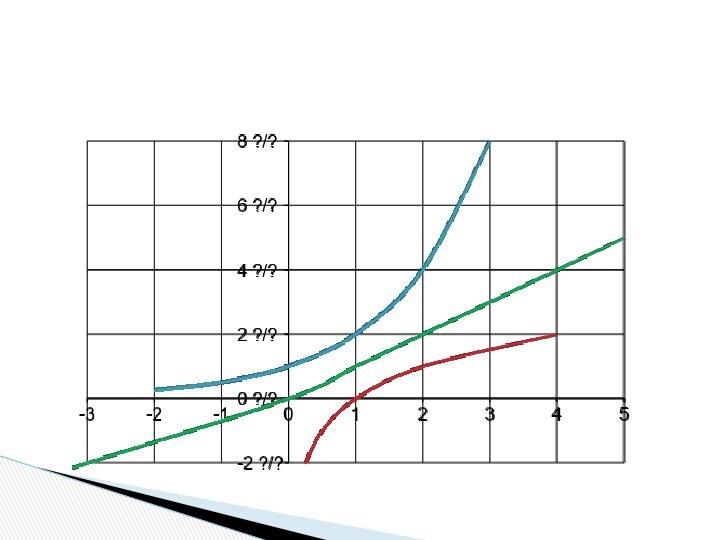
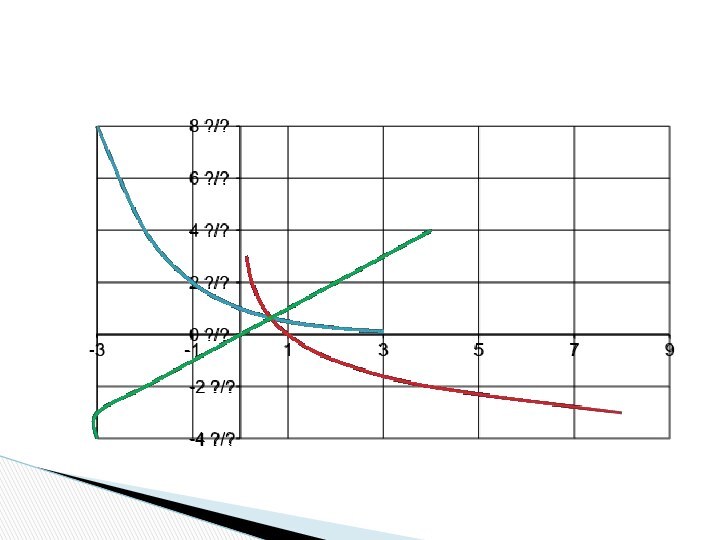
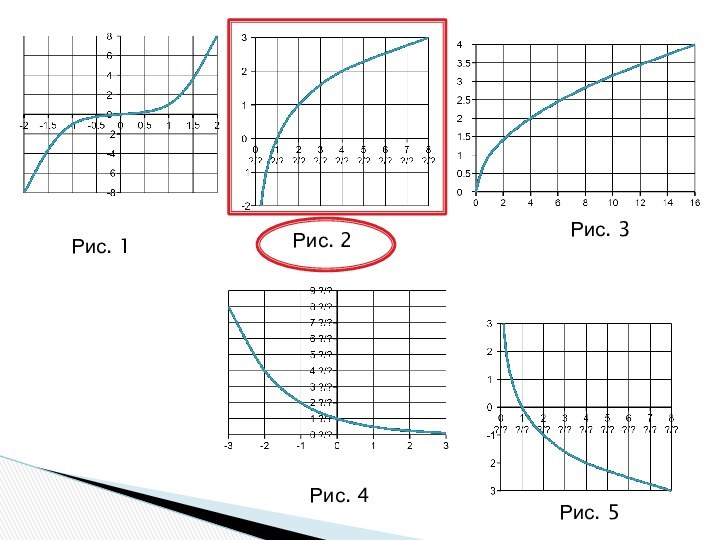
- 2. Графики каких функций представлены на рисунках? Рис. 1Рис. 2y=ax , a>1
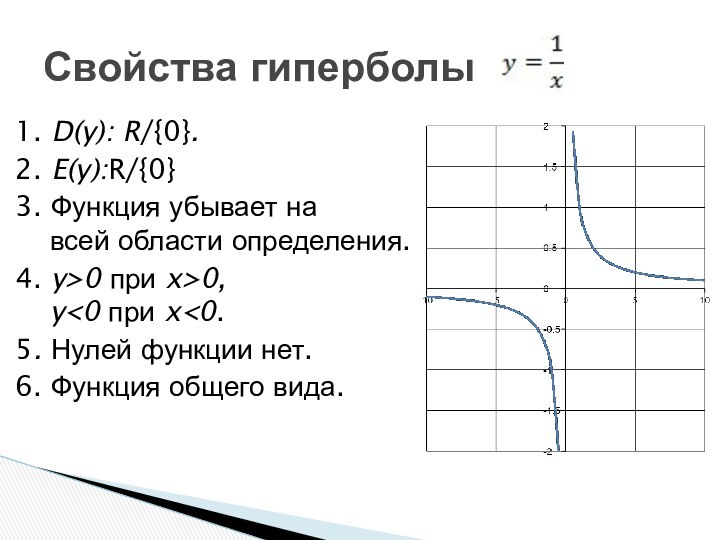
- 3. 1. D(y): R/{0}.2. E(y):R/{0}3. Функция убывает на всей области определения.4. y>0 при x>0, y
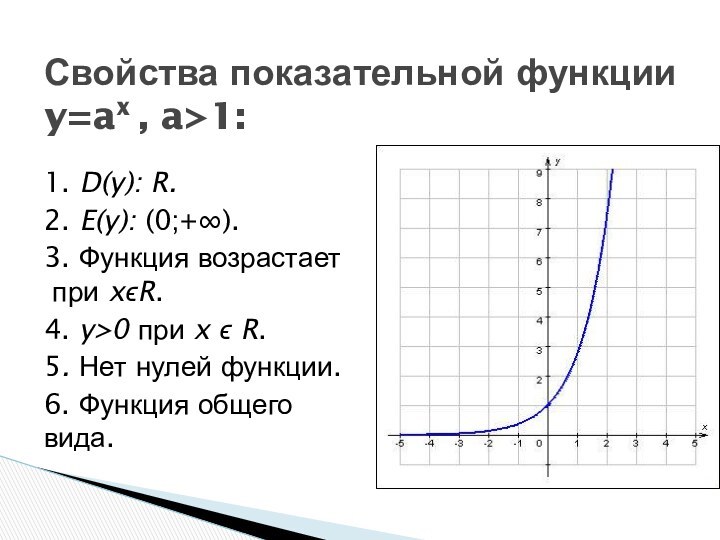
- 4. 1. D(y): R.2. E(y): (0;+∞).3. Функция возрастает
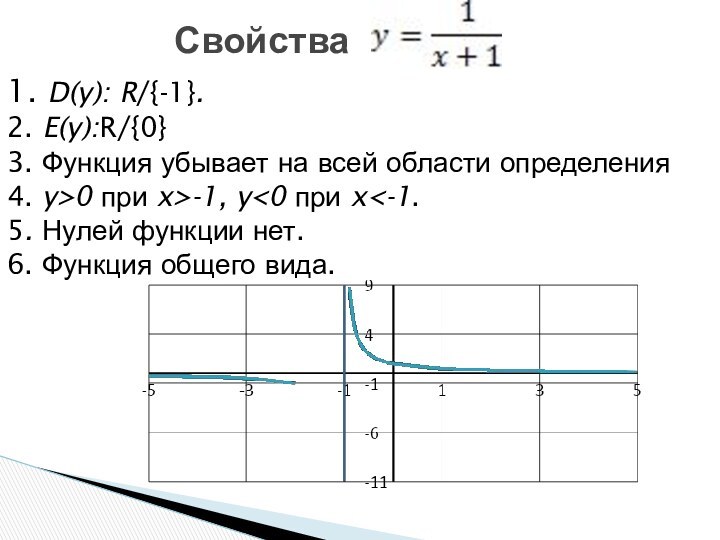
- 5. 1. D(y): R/{-1}.2. E(y):R/{0}3. Функция убывает на всей области определения4. y>0 при x>-1, y
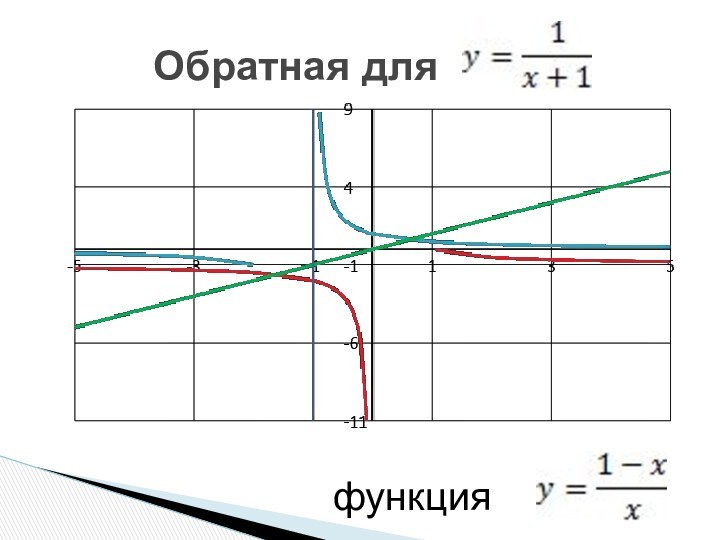
- 6. Обратная для функция
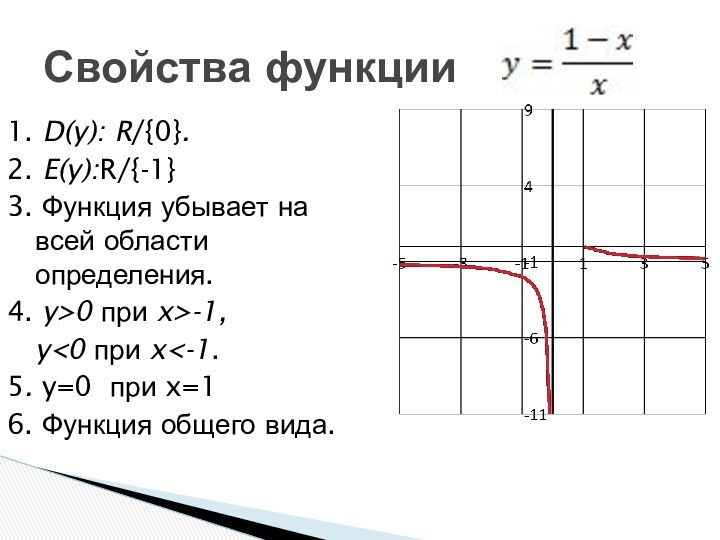
- 7. 1. D(y): R/{0}.2. E(y):R/{-1}3. Функция убывает на всей области определения.4. y>0 при x>-1,y
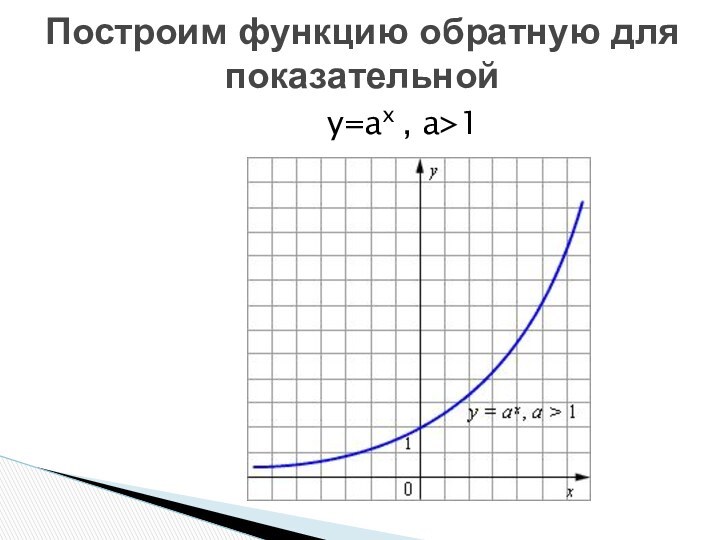
- 8. Построим функцию обратную для показательнойy=ax , a>1
- 10. Свойства функции y= loga x , a>11.
- 11. Логарифмические спирали – это линии в геометрии,
- 12. Вращающиеся ножи нередко имеют профиль, очерченный по
- 13. Рост раковин морских животных происходит по логарифмической спирали. Логарифмическая спираль в природе
- 14. Эта спираль является математическим символом соотношения форм роста.
- 15. Рога архаров закручены по логарифмической спирали.Семечки в
- 16. Паук ЭПЕЙРА, сплетая паутину, закручивает нити вокруг
- 17. Молекула ДНКМолекулы ДНК имеют огромную по молекулярным
- 18. 1. D(y): R.2. E(y): (0;+∞).3. Функция возрастает
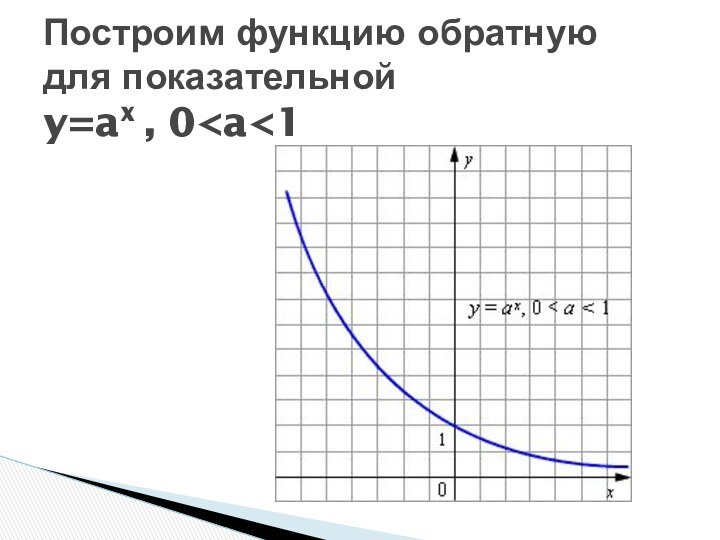
- 19. Построим функцию обратную для показательной y=ax , 0
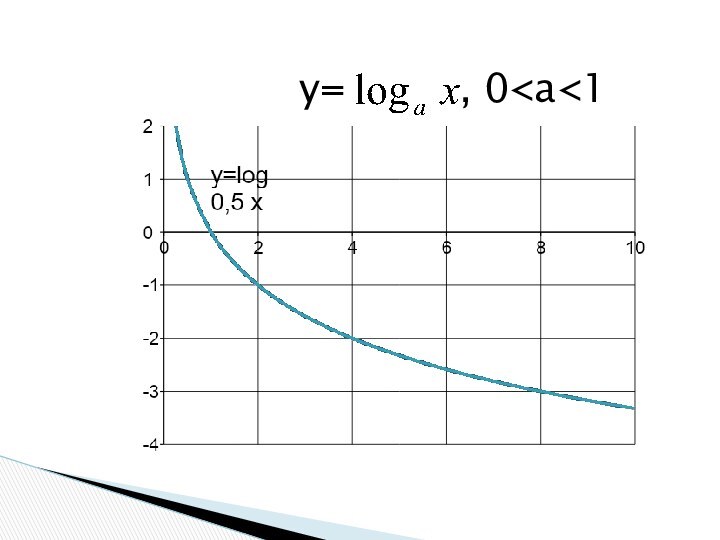
- 21. y= , 0
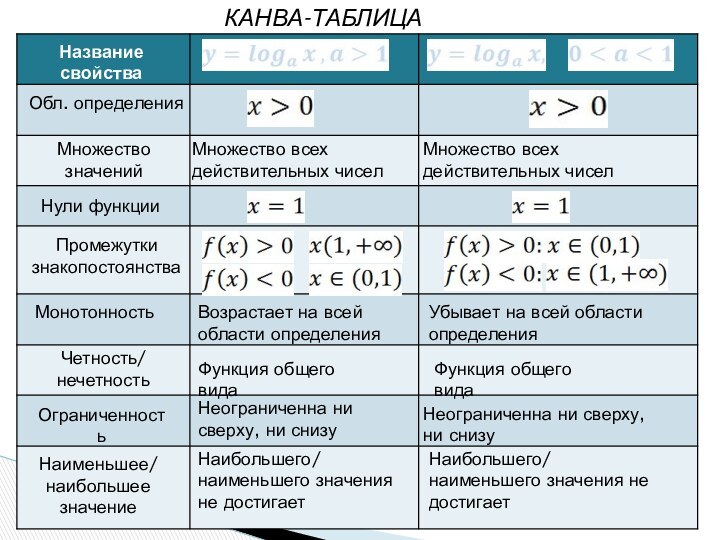
- 22. КАНВА-ТАБЛИЦА Название свойстваОбл. определенияМножество значенийНули функцииПромежутки знакопостоянстваМонотонностьЧетность/нечетностьОграниченностьНаименьшее/наибольшее
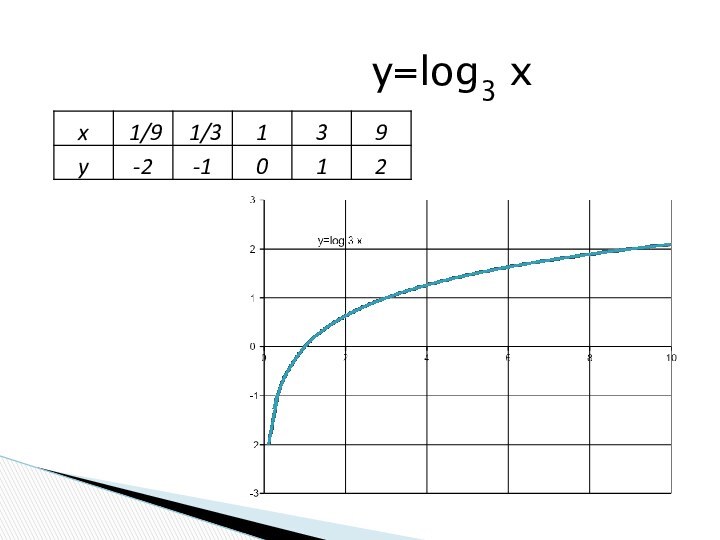
- 23. y=log3 x
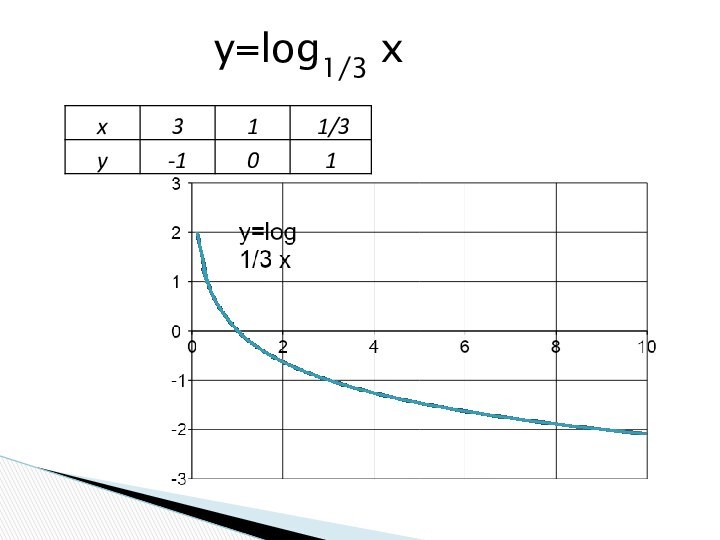
- 24. y=log1/3 x
- 25. Рис. 1Рис. 3Рис. 2Рис. 4Рис. 5
- 26. y=log 125 zНазовите зависимую и независимую переменную .
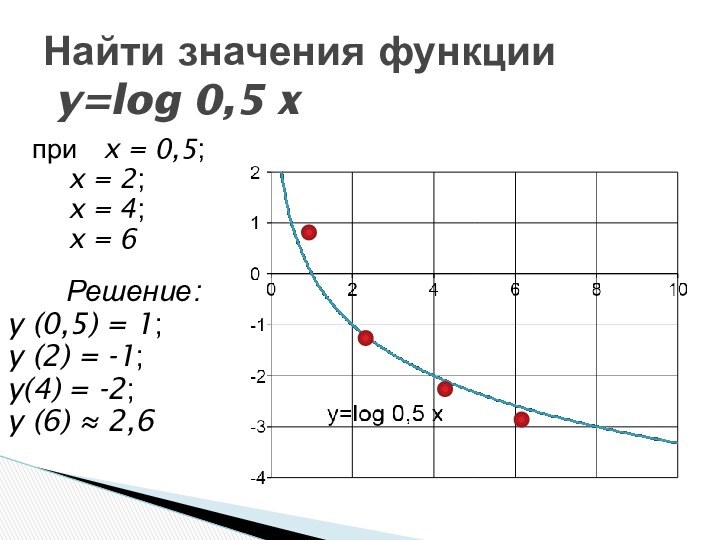
- 27. при x = 0,5; x =
- 28. y=3 y=2y=-1y=-4 По заданному значению функции y=log5 x найти
- 29. По заданному значению функции y=log1/36 x найти
- 30. y=log-0,5 2;y=log7 49;y=log89 (-89);y=log1 9.Является ли функция логарифмической?
- 31. и иСравнить числа:Решение:3>1 и >9
- 32. Скачать презентацию
- 33. Похожие презентации













Слайд 3
1. D(y): R/{0}.
2. E(y):R/{0}
3. Функция убывает на
всей
области определения.
4. y>0 при x>0,
y
функции нет.6. Функция общего вида.
Свойства гиперболы
Слайд 4
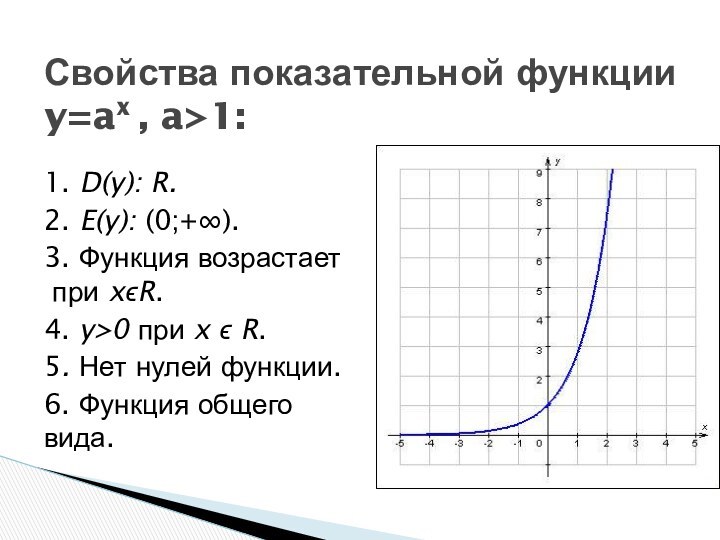
1. D(y): R.
2. E(y): (0;+∞).
3. Функция возрастает
при
xϵR.
4. y>0 при x ϵ R.
5. Нет нулей функции.
6.
Функция общего вида.Свойства показательной функции y=ax , a>1:
Слайд 5
1. D(y): R/{-1}.
2. E(y):R/{0}
3. Функция убывает на всей
области определения
4. y>0 при x>-1, y
функции нет.6. Функция общего вида.
Свойства
Слайд 7
1. D(y): R/{0}.
2. E(y):R/{-1}
3. Функция убывает на всей
области определения.
4. y>0 при x>-1,
y
x=16. Функция общего вида.
Свойства функции
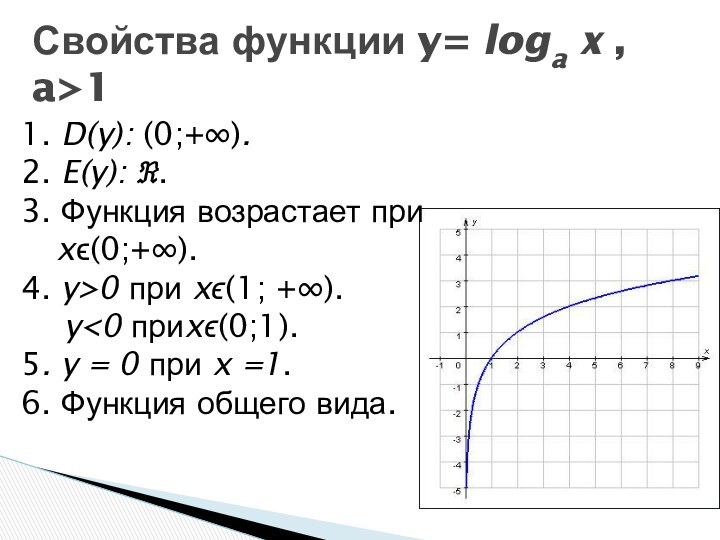
Слайд 10
Свойства функции y= loga x , a>1
1. D(y):
(0;+∞).
2. E(y): .
3. Функция возрастает при xϵ(0;+∞).
4. y>0 при
xϵ(1; +∞).y<0 приxϵ(0;1).
5. y = 0 при x =1.
6. Функция общего вида.
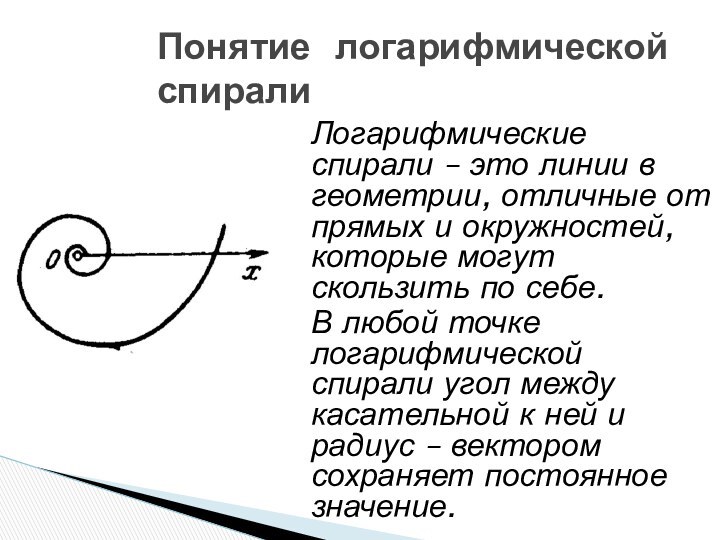
Слайд 11 Логарифмические спирали – это линии в геометрии, отличные
от прямых и окружностей, которые могут скользить по себе.
В любой точке логарифмической спирали угол между касательной к ней и радиус – вектором сохраняет постоянное значение.
Понятие логарифмической спирали
Слайд 12 Вращающиеся ножи нередко имеют профиль, очерченный по логарифмической
спирали – под постоянным углом к разрезаемой поверхности, благодаря
чему лезвие ножа стачивает равномерно.Применение логарифмической спирали в технике
Слайд 13 Рост раковин морских животных происходит по логарифмической спирали.
Логарифмическая спираль в природе
Слайд 15
Рога архаров закручены по логарифмической спирали.
Семечки в подсолнухе
расположены по дугам, так же близким к логарифмической спирали.
Слайд 16 Паук ЭПЕЙРА, сплетая паутину, закручивает нити вокруг центра
по логарифмической спирали.
По логарифмическим спиралям закручены и многие
галактики, в частности, Млечный путь.
Слайд 17
Молекула ДНК
Молекулы ДНК имеют огромную по молекулярным масштабам
длину и состоят из 2-х нитей, сплетённых между собой
в двойную спираль. «Бусины» двух нитей двойной спирали ДНК связаны между собой и строго друг другу соответствуют.
Слайд 18
1. D(y): R.
2. E(y): (0;+∞).
3. Функция возрастает
при
xϵR.
4. y>0 при x ϵ R.
5. Нет нулей функции.
6.
Функция общего вида.Свойства показательной функции y=ax , a>1:
Слайд 22
КАНВА-ТАБЛИЦА
Название свойства
Обл. определения
Множество значений
Нули функции
Промежутки знакопостоянства
Монотонность
Четность/
нечетность
Ограниченность
Наименьшее/
наибольшее
значение
Множество всех действительных чисел
Множество всех действительных чисел
Возрастает на всей
области определенияУбывает на всей области определения
Функция общего вида
Функция общего вида
Неограниченна ни сверху,
ни снизу
Неограниченна ни сверху, ни снизу
Наибольшего/
наименьшего значения не достигает
Наибольшего/
наименьшего значения не достигает
Слайд 27
при x = 0,5;
x = 2;
x
= 4;
x = 6
Найти значения функции
y=log 0,5
x Решение:
y (0,5) = 1;
y (2) = -1;
y(4) = -2;
y (6) 2,6





























