Слайд 2
Векторные величины, характеризующие магнитное поле
Слайд 3
Направление магнитных линий и направление создающего их тока
связаны между собой известным правилом правоходового винта (буравчика) (рис.
1).
Рис. 1. Магнитное поле прямолинейного проводника и катушки. Правило Буравчика
Основной величиной, характеризующей интенсивность и направление магнитного поля является – вектор магнитной индукции , которая измеряется в Теслах [Тл].
Вектор направлен по касательной к магнитной линии, направление вектора совпадает с осью магнитной стрелки, помещенной в рассматриваемую точку магнитного поля.
Величина определяется по механической силе, действующей на элемент проводника с током, помещенный в магнитное поле.
Если во всех точках поля имеет одинаковую величину и направление, то такое поле называется равномерным.
зависит не только от величины I, но и от магнитных свойств окружающей среды.
Слайд 4
Второй важной величиной, характеризующей магнитное поле является –
магнитный поток , который измеряется в Веберах [Вб].
Элементарным магнитным
потоком Ф сквозь бесконечно малую площадку называется величина (рис. 2)
dФ = B cos α dS,
где α – угол между направлением и нормалью к площадке dS.
Рис. 2. Определение магнитного потока, пронизывающего: а) произвольную поверхность; б) плоскую поверхность в равномерном магнитном поле
Сквозь поверхность S [м2]
Ф = s∫ dФ = s∫ B cos α dS,
Если магнитное поле равномерное, а поверхность S представляет собой плоскость
Ф = B S.
Слайд 5
При исследовании магнитных полей и расчете магнитных устройств
пользуются расчетной величиной – напряженность магнитного поля [А/м]
где μа
– абсолютная магнитная проницаемость среды.
Для неферромагнитных материалов и сред (дерево, бумага, медь, алюминий, воздух) μа не отличается от магнитной проницаемости вакуума и равна
μo = 4 p · 10-7, Гн/м (Генри/метр).
У ферромагнетиков μа переменная и зависит от В.
Слайд 6
Характеристики ферромагнитных материалов
Известно, что магнитная проницаемость μа ферромагнитных
материалов переменная величина и зависит от В. Это влечет
за собой непостоянство магнитного сопротивления Rм и значительно усложняет расчеты магнитных цепей. Поэтому для расчета магнитных цепей, содержащих ферромагнитные участки, необходимо располагать кривыми намагничивания, представляющими собой зависимость B = f(H). Эти зависимости получают экспериментальным путем – испытанием замкнутых магнитопроводов с распределенной обмоткой.
Первоначальному намагничиванию образца соответствует кривая a, называемая кривой первоначального намагничивания (рис. 3).
Слайд 7
Процесс циклического перемагничивания требует затраты энергии, как известно
из курса физики, пропорциональной площади петли гистерезиса.
В связи с
этим магнитопроводы электротехнических устройств, работающих в условиях непрерывного перемагничивания (например трансформаторы), целесообразно выполнять из ферромагнитных материалов, имеющих узкую петлю гистерезиса (на рис. 4., кривые a). Такие ферромагнитные материалы называют магнитомягкими (листовая электротехническая сталь и ряд специальных сплавов, например пермаллой, состоящий из никеля, железа и других компонентов).
Для изготовления постоянных магнитов рекомендуется использовать ферромагнитные материалы с широкой петлей гистерезиса (кривые δ), имеющих большую остаточную индукцию и большую коэрцетивную силу. Такие ферромагнитные материалы называют магнитотвердыми (ряд сплавов железа с вольфрамом, хромом и алюминием
Слайд 8
Статическая и дифференциальная магнитные проницаемости
Статическая магнитная проницаемость (в
справочниках начальная и максимальная)
определяется по основной кривой намагничивания и в силу
ее нелинейности не постоянна по величине (см. рис. 5).
Величина определяется тангенсом угла наклона касательной в начале кривой .
Кроме статической вводится понятие дифференциальной магнитной проницаемости, устанавливающей связь между бесконечно малыми приращениями индукции и напряженности
.
Кривые и имеют две общие точки: начальную и точку, соответствующую максимуму
При учете петли гистерезиса статическая магнитная проницаемость, теряет смысл. При этом значения определяют по восходящей ветви петли при и по нисходящей – при .
Слайд 9
Основные законы магнитной цепи
Слайд 10
Законы Кирхгофа и Ома для магнитных цепей
Слайд 11
Аналогия величин и законов для электрических и магнитных
цепей
Слайд 12
В конструкцию многих электротехнических устройств (электрических машин, трансформаторов,
электрических аппаратов, измерительных приборов и т.д.) входят магнитные цепи.
Магнитной
цепью называется часть электротехнического устройства, содержащая ферромагнитные тела, в которой, при наличии намагничивающёй силы возникает магнитный поток и вдоль которой замыкаются линии магнитной индукции.
Источниками намагничивающей силы могут быть катушки с токами, постоянные магниты.
В конструктивном отношении магнитные цепи выполняют разветвленными и неразветвленными; применение того или иного вида цепи определяется в основном назначением электромагнитного устройства.
Слайд 13
Магнитная цепь
Неразветвленная
Разветвленная
Однородная
Неоднородная
Симметричная
Несимметричная
Слайд 14
Прямая задача
Задано: 1) геометрические размеры магнитной цепи; 2) характеристика B = f(H)
(кривая намагничивания) ферромагнитных материалов, из которых выполнена магнитная цепь;
3) магнитный поток Ф, который надо создать в магнитной цепи. Требуется найти намагничивающую силу обмотки F = IW.
Слайд 16
Обратная задача
Задано:
Геометрические размеры магнитной цепи;
Характеристики ферромагнитных материалов;
Намагничивающая сила
обмотки F.
Требуется определить магнитный поток Ф.
.
Слайд 18
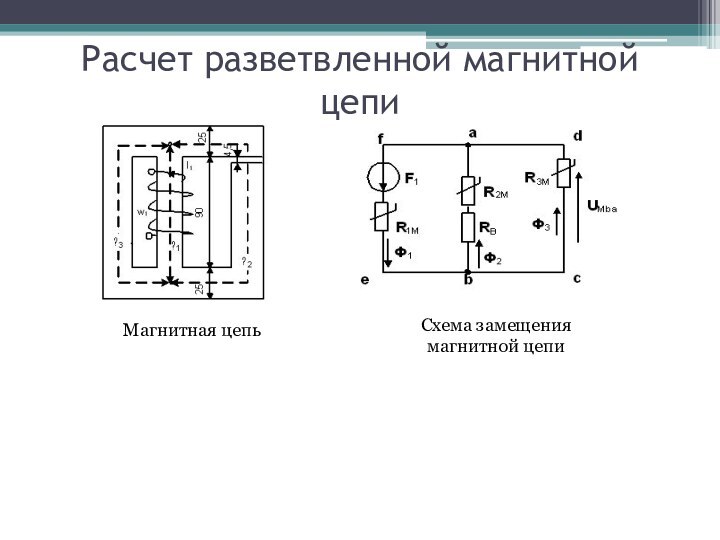
Расчет разветвленной магнитной цепи
Магнитная цепь
Схема замещения магнитной цепи
Слайд 19
Составляем уравнения.
Примем, что втекающие магнитные потоки будут
записаны со знаком минус, а вытекающие – с плюсом.
Тогда для узла а по первому закону Кирхгофа для магнитной цепи получаем:
Ф1–Ф2–Ф3=0.
Запишем уравнения по второму закону Кирхгофа для контуров afebcda и аbcda. Обход контура и в том и в другом случае выбираем против обхода часовой стрелки.
afebcda: F1=H1ℓ1+UMba
аbcda: 0=–H2ℓ2–H0ℓ0+UMba,
UMba=H3ℓ3.
где H1, H2, H3, H0, ℓ1, ℓ2, ℓ3, ℓ0 – напряженности магнитного поля и средние линии участков магнитной цепи, соответственно, первой, второй, третьей ветвей магнитопровода и воздушного зазора,
F1=I1w1 –магнитодвижущая сила.
Слайд 20
Полученная в система нелинейных уравнений может быть решена
графоаналитическим методом. Для этого необходимо будет построить зависимости магнитных
потоков от магнитного напряжения UMba: Ф1=f(UMba), Ф2=f(UMba), Ф3=f(UMba). Поскольку по первому закону Кирхгофа Ф1=Ф2+Ф3, то необходимо будет построить и суммарную кривую магнитных потоков Ф2 и Ф3 при одних и тех же значениях магнитного напряжения UMbа. Точка пересечения суммарной кривой и Ф1=f(UMba) определит значения магнитного потока Ф1 и магнитного напряжения UMbа. Зная значения UMbа, по построенным кривым Ф2=f(UMba) и Ф3=f(UMba) можно определить магнитные потоки Ф2 и Ф3.