Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

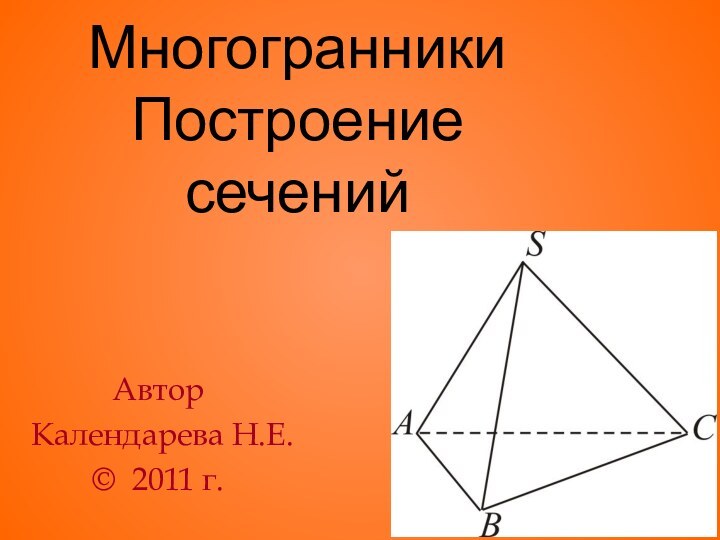
Презентация на тему МногогранникиПостроениесечений

Содержание

2. ПланПерпендикулярность прямыхПерпендикулярность прямой и плоскостиКуб, его параллельные плоскости и прямыеТреугольная пирамидаПостроение сечений
3. Перпендикулярность пря- мых в пространствеДве прямые называются перпендикулярными, если они пересекаются под прямым углом.
4. Перпендикулярность пря- мой и плоскостиПрямая, пересекающая плоскость,
5. МногогранникМногогранник – это такое тело, поверхность которого
6. Стороны граней называются ребрами многогранника, а вершины
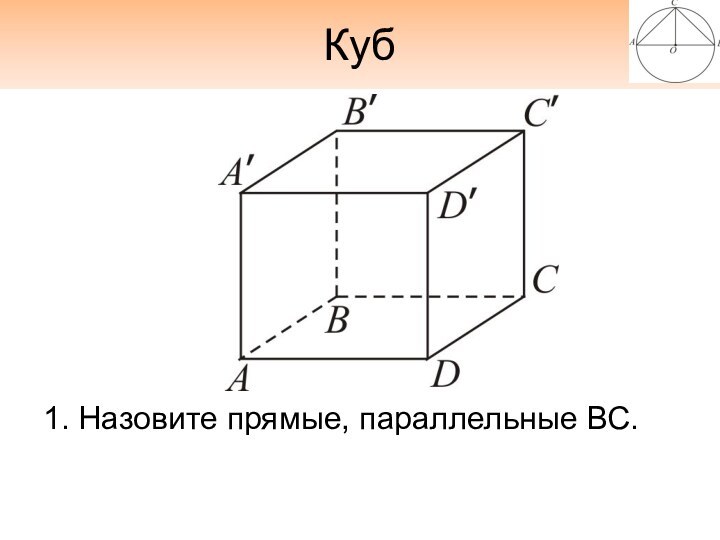
7. Куб1. Назовите прямые, параллельные ВС.
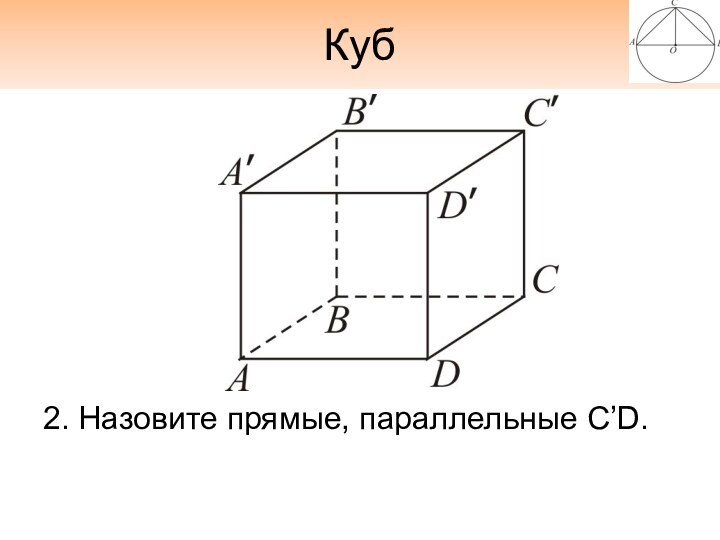
8. Куб2. Назовите прямые, параллельные C’D.
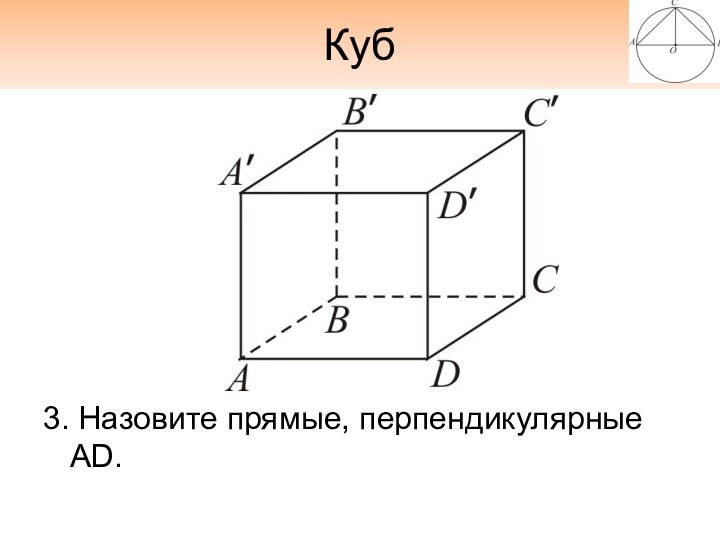
9. Куб3. Назовите прямые, перпендикулярные AD.
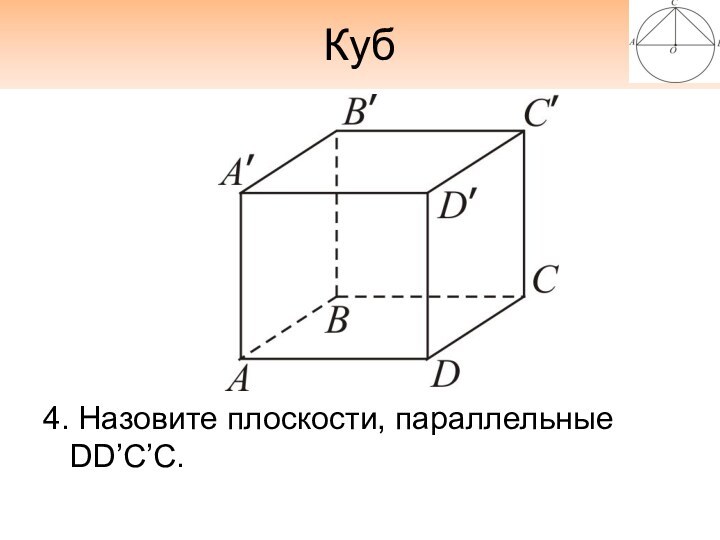
10. Куб4. Назовите плоскости, параллельные DD’C’С.
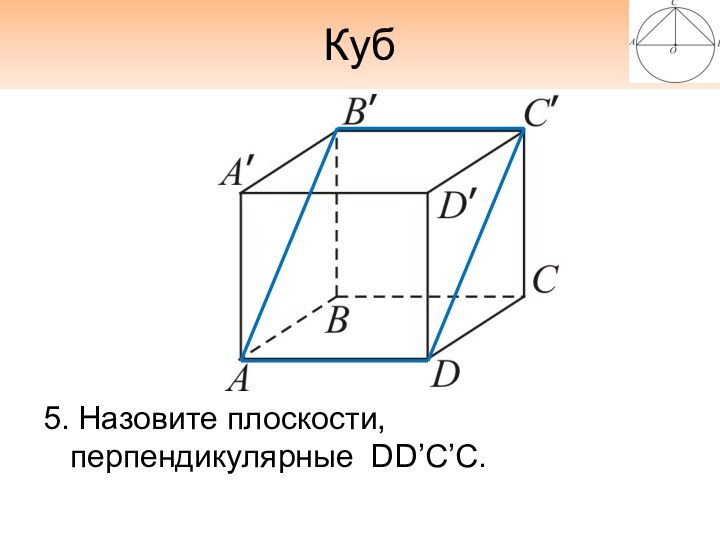
11. Куб5. Назовите плоскости, перпендикулярные DD’C’С.
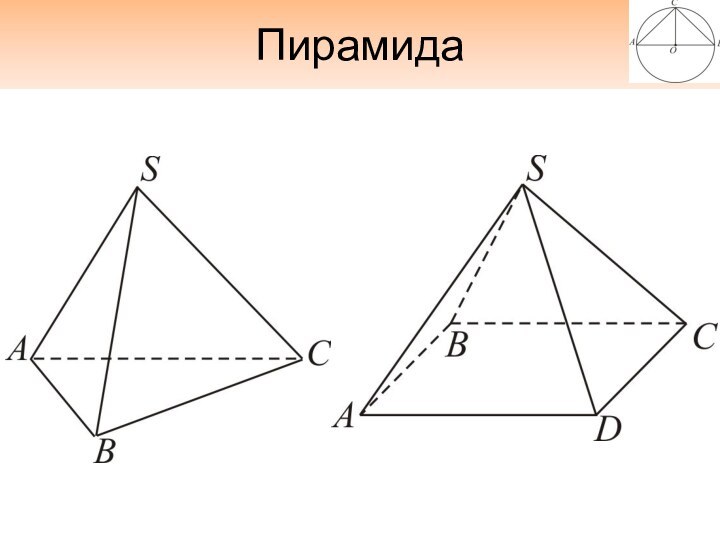
12. Пирамида
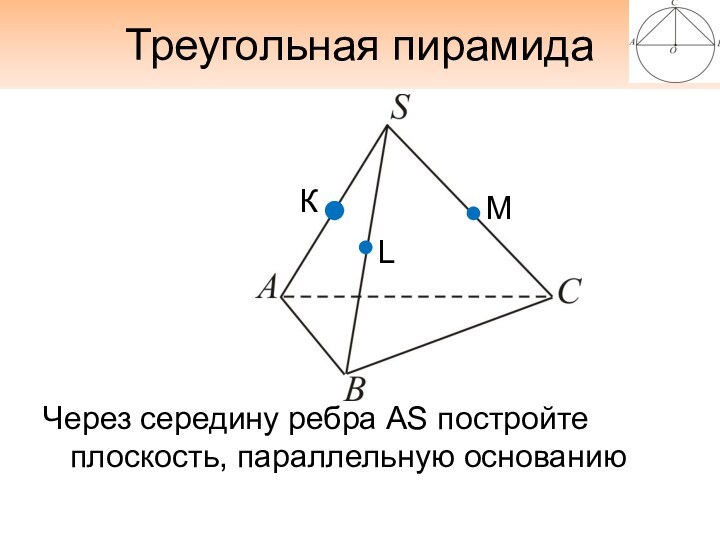
13. Треугольная пирамидаЧерез середину ребра AS постройте плоскость, параллельную основанию
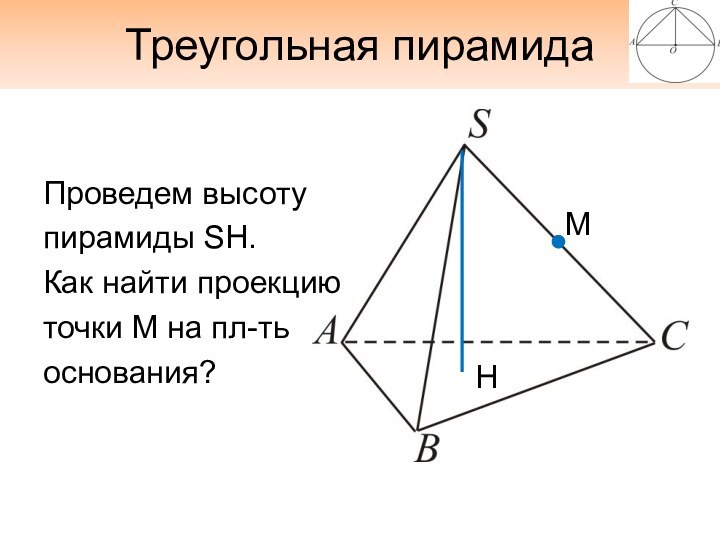
14. Треугольная пирамидаПроведем высотупирамиды SH.Как найти проекциюточки М на пл-тьоснования?HM
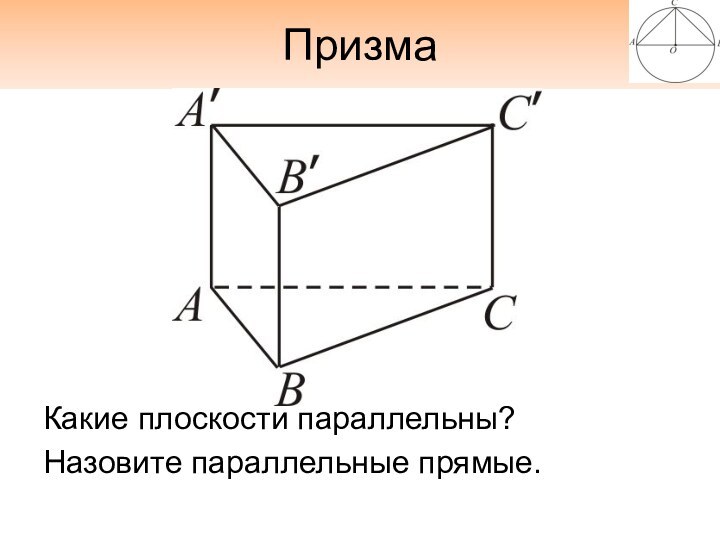
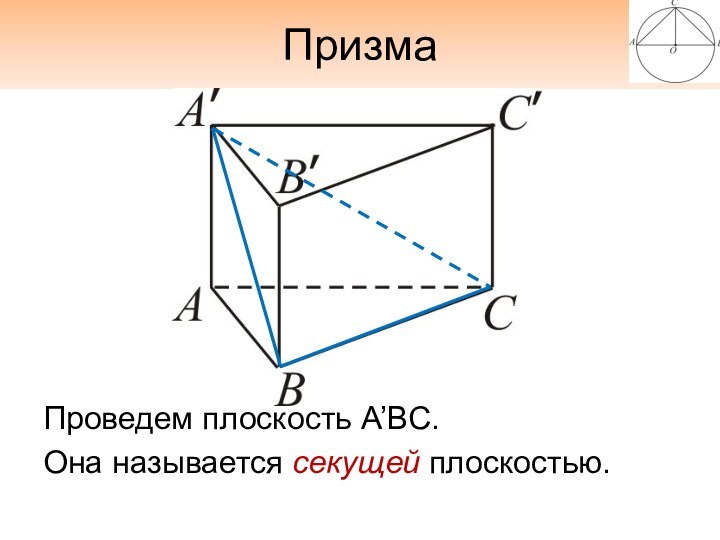
15. ПризмаКакие плоскости параллельны?Назовите параллельные прямые.
16. ПризмаПроведем плоскость A’BC. Она называется секущей плоскостью.
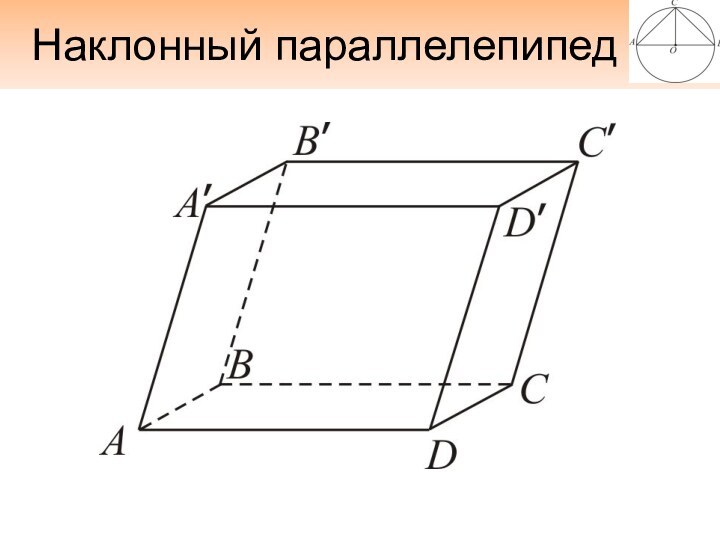
17. Наклонный параллелепипед
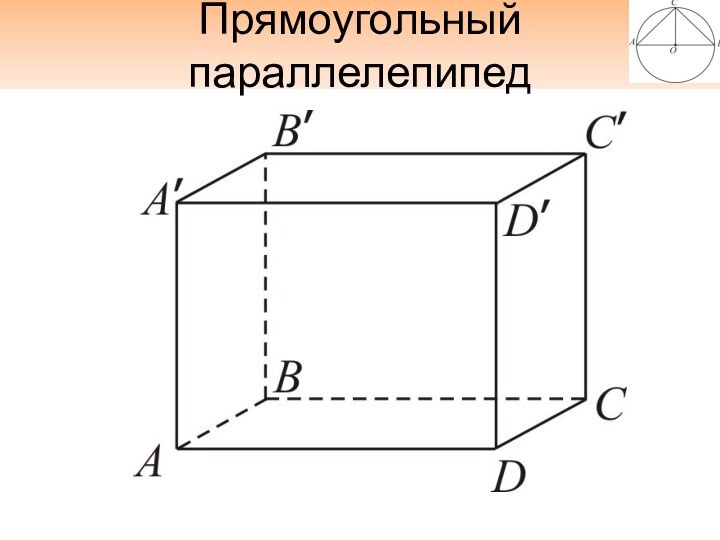
18. Прямоугольный параллелепипед
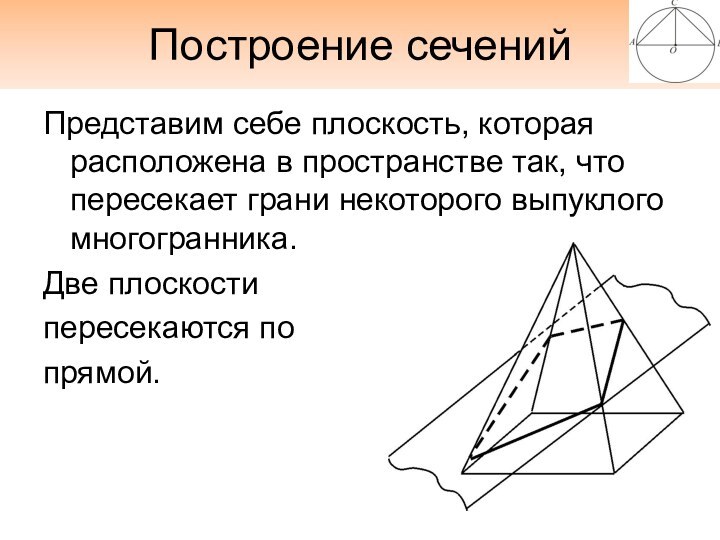
19. Построение сеченийПредставим себе плоскость, которая расположена в
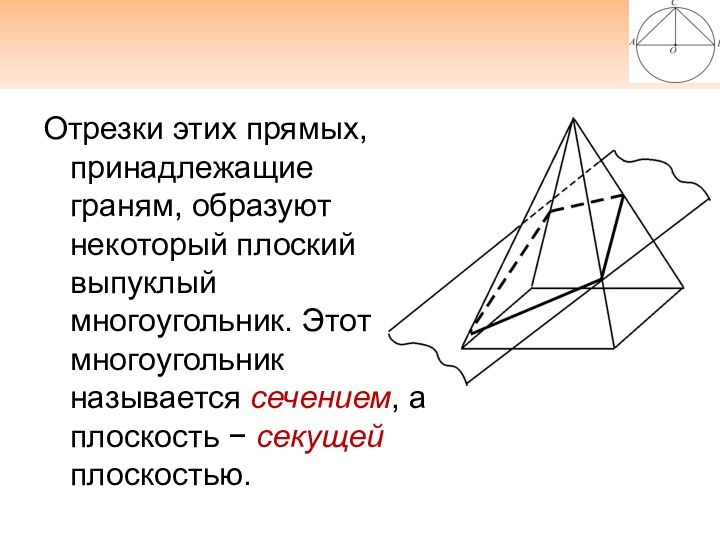
20. Отрезки этих прямых, принадлежащие граням, образуют некоторый
21. В задачах на построение сечений требуется построить
22. Теоретический материалАксиома С2Если две различные плоскости имеют
23. Необходимые теоремыЧерез три точки, не лежащие на
24. Метод следовДля построения сечений используют обычно два метода: метод следов и метод проекций.Рассмотрим метод следов.
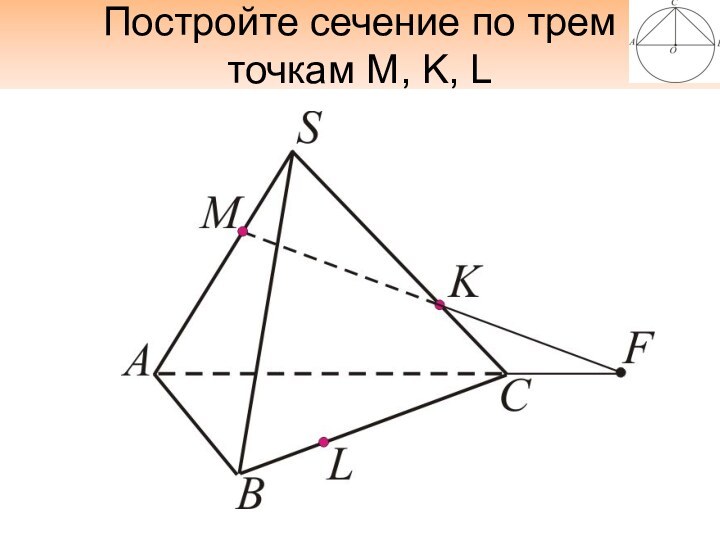
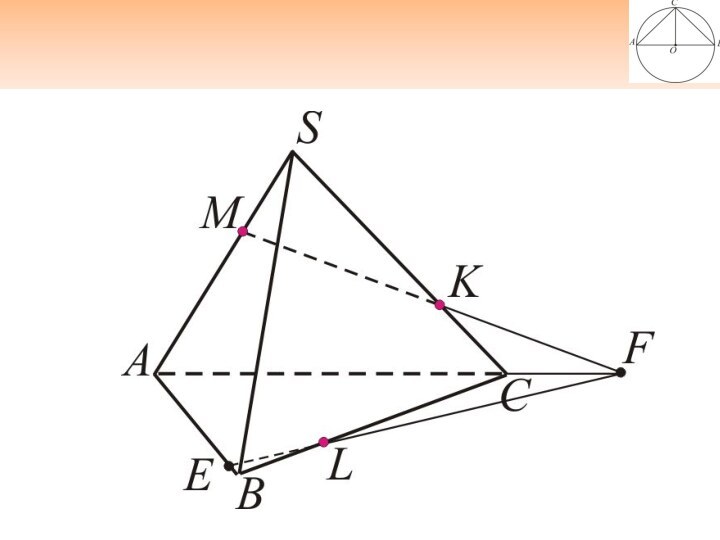
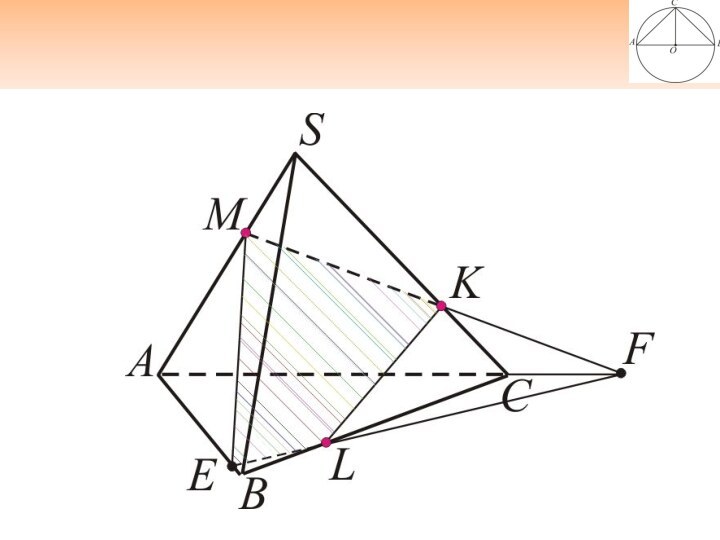
25. Постройте сечение по трем точкам M, K, L
28. Постройте сечение по трем точкам E, F,
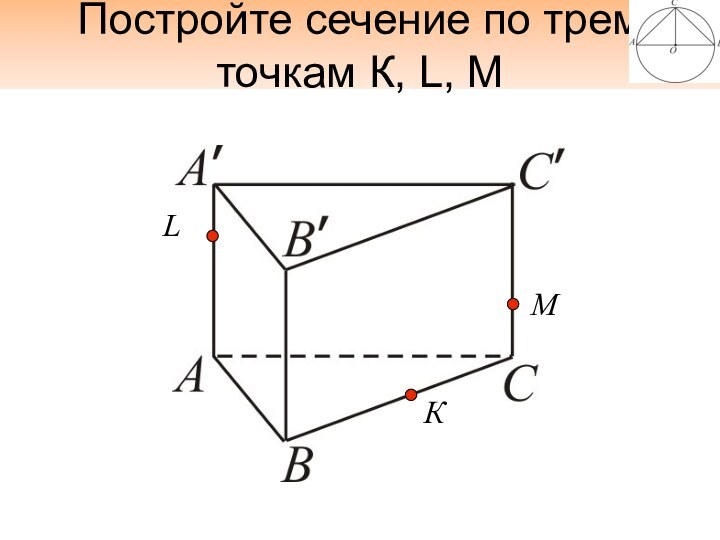
29. Постройте сечение по трем точкам К, L, М
30. ЛитератураУчебник по геометрии под ред. ПогореловаКалендарева С.Т. Построение сечений многогранников. Метод. пособие
31. Скачать презентацию
32. Похожие презентации

ПланПерпендикулярность прямыхПерпендикулярность прямой и плоскостиКуб, его параллельные плоскости и прямыеТреугольная пирамидаПостроение сечений

Главная
Разное
МногогранникиПостроениесечений

Многогранники Построение сечений Автор Календарева Н.Е.© 2011 г.

ПланПерпендикулярность прямыхПерпендикулярность прямой и плоскостиКуб, его параллельные плоскости и прямыеТреугольная пирамидаПостроение сечений

Перпендикулярность пря- мых в пространствеДве прямые называются перпендикулярными, если они пересекаются под прямым углом.

Перпендикулярность пря- мой и плоскостиПрямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если

МногогранникМногогранник – это такое тело, поверхность которого состоит из конечного числа плоских

Стороны граней называются ребрами многогранника, а вершины – вершинами многогранника.Примеры многогранников:куб, пирамида,

Куб2. Назовите прямые, параллельные C’D.

Куб3. Назовите прямые, перпендикулярные AD.

Куб4. Назовите плоскости, параллельные DD’C’С.

Куб5. Назовите плоскости, перпендикулярные DD’C’С.

Треугольная пирамидаЧерез середину ребра AS постройте плоскость, параллельную основанию

Треугольная пирамидаПроведем высотупирамиды SH.Как найти проекциюточки М на пл-тьоснования?HM

ПризмаКакие плоскости параллельны?Назовите параллельные прямые.

ПризмаПроведем плоскость A’BC. Она называется секущей плоскостью.

Построение сеченийПредставим себе плоскость, которая расположена в пространстве так, что пересекает грани

Отрезки этих прямых, принадлежащие граням, образуют некоторый плоский выпуклый многоугольник. Этот многоугольник

В задачах на построение сечений требуется построить этот многоугольник, т.е. найти отрезки,

Теоретический материалАксиома С2Если две различные плоскости имеют общую точку, то они пересекаются

Необходимые теоремыЧерез три точки, не лежащие на одной прямой, можно провести плоскость,

Метод следовДля построения сечений используют обычно два метода: метод следов и метод проекций.Рассмотрим метод следов.

Постройте сечение по трем точкам M, K, L

Постройте сечение по трем точкам E, F, GAE : EC = 1

Постройте сечение по трем точкам К, L, М

ЛитератураУчебник по геометрии под ред. ПогореловаКалендарева С.Т. Построение сечений многогранников. Метод. пособие

Слайды презентации

Слайд 2 План
Перпендикулярность прямых
Перпендикулярность прямой и плоскости
Куб, его параллельные плоскости

и прямые
Треугольная пирамида
Построение сечений

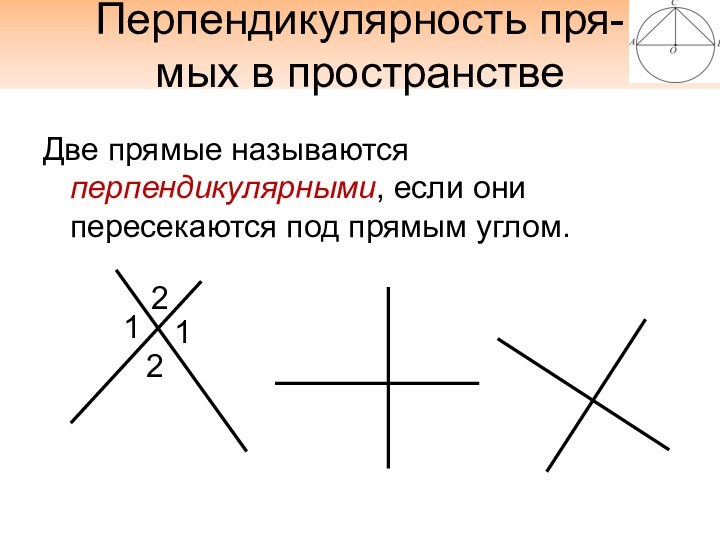
Слайд 3 Перпендикулярность пря- мых в пространстве
Две прямые называются перпендикулярными, если

они пересекаются под прямым углом.

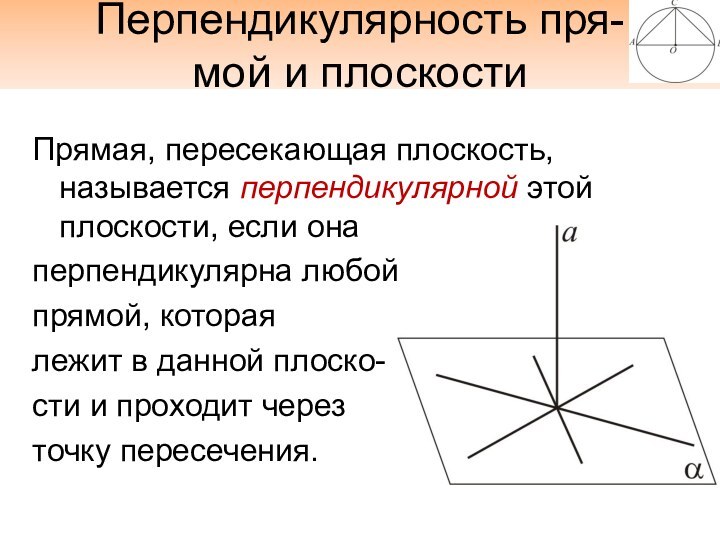
Слайд 4 Перпендикулярность пря- мой и плоскости
Прямая, пересекающая плоскость, называется перпендикулярной

Перпендикулярность пря- мой и плоскостиПрямая, пересекающая плоскость, называется перпендикулярной этой плоскости,

этой плоскости, если она
перпендикулярна любой
прямой, которая
лежит в данной плоско-
сти

и проходит через
точку пересечения.

Слайд 5 Многогранник
Многогранник – это такое тело, поверхность которого состоит

МногогранникМногогранник – это такое тело, поверхность которого состоит из конечного числа

из конечного числа плоских многоугольников.
Многогранник называется выпуклым, если он

расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности.
Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью.

Слайд 6 Стороны граней называются ребрами многогранника, а вершины –

Стороны граней называются ребрами многогранника, а вершины – вершинами многогранника.Примеры многогранников:куб,

вершинами многогранника.
Примеры многогранников:
куб, пирамида, призма, параллелепипед.
Треугольная пирамида называется также

тетраэдром.

Слайд 7 Куб

1. Назовите прямые, параллельные ВС.

Слайд 8 Куб

2. Назовите прямые, параллельные C’D.

Слайд 9 Куб

3. Назовите прямые, перпендикулярные AD.

Слайд 10 Куб

4. Назовите плоскости, параллельные DD’C’С.

Слайд 11 Куб

5. Назовите плоскости, перпендикулярные DD’C’С.

Слайд 12 Пирамида

Слайд 13 Треугольная пирамида

Через середину ребра AS постройте плоскость, параллельную

основанию

Слайд 14 Треугольная пирамида

Проведем высоту
пирамиды SH.
Как найти проекцию
точки М на

пл-ть
основания?
H
M

Слайд 15 Призма

Какие плоскости параллельны?
Назовите параллельные прямые.

Слайд 16 Призма

Проведем плоскость A’BC.
Она называется секущей плоскостью.

Слайд 17 Наклонный параллелепипед

Слайд 18 Прямоугольный параллелепипед

Слайд 19 Построение сечений
Представим себе плоскость, которая расположена в пространстве

Построение сеченийПредставим себе плоскость, которая расположена в пространстве так, что пересекает

так, что пересекает грани некоторого выпуклого многогранника.
Две плоскости
пересекаются по
прямой.

Слайд 20 Отрезки этих прямых, принадлежащие граням, образуют некоторый плоский

Отрезки этих прямых, принадлежащие граням, образуют некоторый плоский выпуклый многоугольник. Этот

выпуклый многоугольник. Этот многоугольник называется сечением, а плоскость 

секущей плоскостью.

Слайд 21 В задачах на построение сечений требуется построить этот

В задачах на построение сечений требуется построить этот многоугольник, т.е. найти

многоугольник, т.е. найти отрезки, по которым секущая плоскость пересекает

грани многогранника.
Секущая плоскость бывает задана тремя точками, точкой и прямой или задана более сложным образом, например, точкой и параллельно некоторым прямым.

Слайд 22 Теоретический материал
Аксиома С2
Если две различные плоскости имеют общую

Теоретический материалАксиома С2Если две различные плоскости имеют общую точку, то они

точку, то они пересекаются по прямой, проходящей через эту

точку.
Следствие из аксиом
Если две плоскости имеют две общие точки, то прямая, проходящая через эти точки, является прямой пересечения данных плоскостей.

Слайд 23 Необходимые теоремы
Через три точки, не лежащие на одной

Необходимые теоремыЧерез три точки, не лежащие на одной прямой, можно провести

прямой, можно провести плоскость, и притом только одну.
Если две

точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.

Слайд 24 Метод следов
Для построения сечений используют обычно два метода:

метод следов и метод проекций.
Рассмотрим метод следов.

Слайд 25 Постройте сечение по трем точкам M, K, L

Слайд 26

Слайд 27

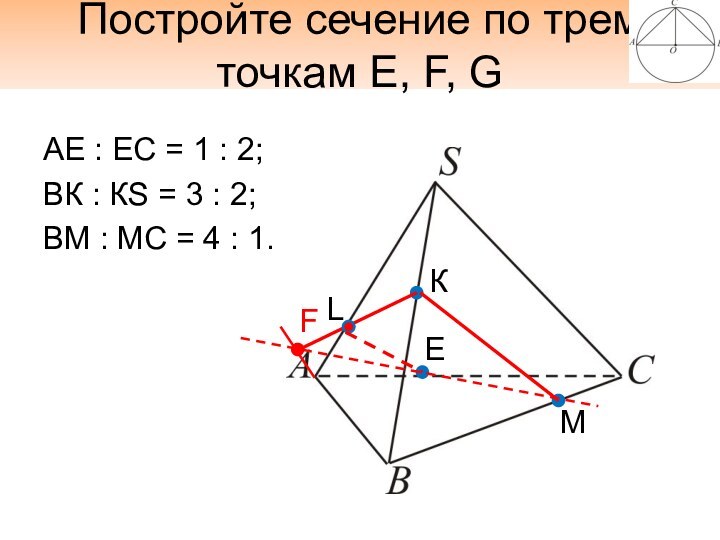
Слайд 28 Постройте сечение по трем точкам E, F, G
AE

Постройте сечение по трем точкам E, F, GAE : EC =

: EC = 1 : 2;
BК : КS =

3 : 2;
BМ : МC = 4 : 1.

Слайд 29 Постройте сечение по трем точкам К, L, М

Слайд 30 Литература
Учебник по геометрии под ред. Погорелова
Календарева С.Т. Построение

сечений многогранников. Метод. пособие

- Предыдущая Роль информационной деятельности в современном обществе

Следующая - История Чичикова

Экономический рост 82

Мужская серия gillette 279

Презентация к року на тему: Имитационное моделирование 112

ПК 4.5. презентация к уроку 54

Центр Европейского Союза в Балтийском федеральном университете имени Иммануила Канта 116

Методическое пособие Стихи детям книга (старшая группа) 120

Внесок народів світу в історію людства. Стародавній Китай . 96

Передняя брюшная стенка 115

Презентация: ИКТ как средство взаимодействия с родителями в группе ДОУ презентация 118

Типовые узлы системы автоматического регулирования 132

Краткосрочный творческий проект по теме: Развитие познавательного интереса у детей через экспериментирование в средней группе детского сада. презентация к уроку (средняя группа) 92

Бюджетирование в системе управленческого учета 106

Родительское собрание Нормы оценивания при проверке контрольных и самостоятельных работ учащихся материал 129

razvitie - 1 chast 124

Презентация родительского собрания на тему Сетевой город (1 класс) 130

Беседа о толерантности презентация к уроку (старшая группа) 100

ЭОР Иллюстрированные считалочки электронный образовательный ресурс 57

Портфолио участника профессионального конкурса Лучший педагог комплекса презентация 95

Силовые трансформаторы 142

Парламентский урок презентация к уроку (3 класс) 130

Повести покойного Ивана Петровича Белкина 92

Консультация для педагогов ДОУ Содержание психолого-педагогической работы по освоению образовательной области Чтение художественной литературы презентация к уроку по теме 108

Родительское собрание Впереди 5-ый класс презентация к уроку (4 класс) по теме 114

Как создать контент, который вызывает устойчивый интерес читателей? 101

Что такое findslide.org?

Обратная связь

Презентация на тему МногогранникиПостроениесечений

Содержание

Слайд 2 ПланПерпендикулярность прямыхПерпендикулярность прямой и плоскостиКуб, его параллельные плоскости

и прямыеТреугольная пирамидаПостроение сечений

Слайд 3 Перпендикулярность пря- мых в пространствеДве прямые называются перпендикулярными, если

они пересекаются под прямым углом.

Слайд 4 Перпендикулярность пря- мой и плоскостиПрямая, пересекающая плоскость, называется перпендикулярной

этой плоскости, если онаперпендикулярна любойпрямой, котораялежит в данной плоско-сти

Слайд 5 МногогранникМногогранник – это такое тело, поверхность которого состоит

из конечного числа плоских многоугольников.Многогранник называется выпуклым, если он

Слайд 6 Стороны граней называются ребрами многогранника, а вершины –

вершинами многогранника.Примеры многогранников:куб, пирамида, призма, параллелепипед.Треугольная пирамида называется также

Слайд 7 Куб1. Назовите прямые, параллельные ВС.

Слайд 8 Куб2. Назовите прямые, параллельные C’D.

Слайд 9 Куб3. Назовите прямые, перпендикулярные AD.

Слайд 10 Куб4. Назовите плоскости, параллельные DD’C’С.

Слайд 11 Куб5. Назовите плоскости, перпендикулярные DD’C’С.