Слайд 2
Обобщение понятия импликации на нечеткие множества
Пусть A и
B - нечеткие высказывания и
соответствующие им функции принадлежности.
Тогда импликации будет соответствовать некоторая функция принадлежности .
По аналогии с традиционной логикой можно предположить, что
Замечание. Это не единственное обобщение оператора импликации.
Под способом определения нечеткой импликации «Если A то B», где A и B – нечеткие множества на X,Y соответственно, будем понимать способ задания нечеткого отношения R на X×Y, соответствующего данному высказыванию.
Слайд 3
Интерпретации понятия импликации
Слайд 6
Композиционное правило вывода
Слайд 7
Композиционное правило вывода
Слайд 8
Обобщенное правило modus ponens (generalized modus ponens)
Обобщенное правило
modus ponens:
Приведенная формулировка имеет два отличия от традиционной формулировки
правила modus ponens :
во-первых, здесь допускается, что - нечеткие множества, и,
во-вторых, необязательно идентично .
Слайд 9
Нечеткие экспертные системы
Слайд 11
Логико-лингвистические системы
В основе построения логико-лингвистических систем лежит композиционное
правило вывода Заде.
Преимущество данной модели - в ее универсальности.
Нам неважно, что именно на входе — конкретные числовые значения или некоторая неопределенность, описываемая нечетким множеством. Но за данную универсальность приходится расплачиваться сложностью системы — нам приходится работать в пространстве размерности m×n. Поэтому общей моделью на практике пользуются довольно редко.
Обычно используют ее упрощенный вариант, называемый нечетким выводом.
Он основывается на предположении, что все входные лингвистические переменные имеют известные нам числовые значения (как и бывает довольно часто на практике).
Также обычно не используют более одной выходной лингвистической переменной.
Слайд 12
Нечеткий логический вывод
Как операцию композиции, так и
операцию импликации можно реализовать по-разному (при этом будет отличаться
и полученный результат), но в любом случае общий логический вывод осуществляется за 4 этапа.
Слайд 13
Нечеткий логический вывод (Основные этапы)
1) этап фаззификации.
С помощью функций принадлежности всех термов входных лингвистических переменных
и на основании задаваемых четких значений из универсумов входных лингвистических переменных определяются степени уверенности в том, что выходная лингвистическая переменная принимает конкретное значение.
Эта степень уверенности есть ордината точки пересечения графика функции принадлежности терма и прямой x=четкое значение ЛП.
Слайд 14
Нечеткий логический вывод (Основные этапы)
2) этап непосредственного нечеткого

вывода. На основании набора правил — нечеткой базы знаний
— вычисляется значение истинности для предпосылки каждого правила на основании конкретных нечетких операций, соответствующих конъюнкции или дизъюнкции термов в левой части правил.
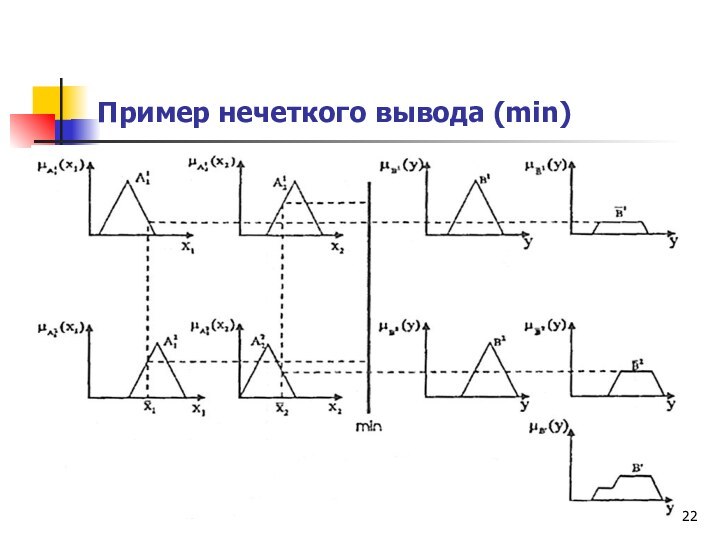
В большинстве случаев это либо максимум, либо минимум из степеней уверенности термов, вычисленных на этапе фаззификации, который применяется к заключению каждого правила. Используя один из способов построения нечеткой импликации, мы получим нечеткую переменную, соответствующую вычисленному значению степени уверенности в левой части правила и нечеткому множеству в правой части правила.
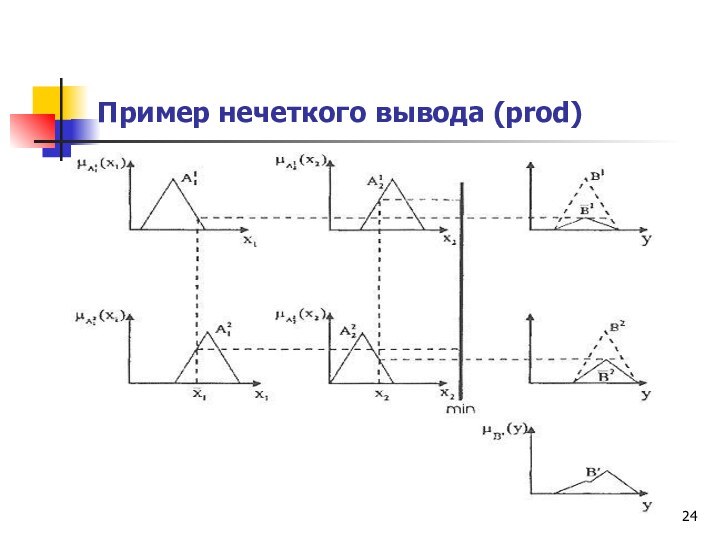
Обычно в качестве вывода используется минимизация или правила продукции. При минимизирующем логическом выводе выходная функция принадлежности ограничена сверху в соответствии с вычисленной степенью истинности посылки правила (нечеткое логическое И). В логическом выводе с использованием продукции выходная функция принадлежности масштабируется с помощью вычисленной степени истинности предпосылки правила.
Слайд 15
Нечеткий логический вывод (Основные этапы)
3) этап композиции (агрегации,
аккумуляции). Все нечеткие множества, назначенные для каждого терма каждой
выходной лингвистической переменной, объединяются вместе, и формируется единственное нечеткое множество — значение для каждой выводимой лингвистической переменной. Обычно используются функции MAX или SUM.
4) этап дефаззификации (необязательный). Используется тогда, когда полезно преобразовать нечеткий набор значений выводимых лингвистических переменных к точным. Имеется достаточно большое количество методов перехода к точным значениям (по крайней мере, 30). Два примера общих методов — "методы полной интерпретации" и "по максимуму". В методе полной интерпретации точное значение выводимой переменной вычисляется как значение "центра тяжести" функции принадлежности для нечеткого значения. В методе максимума в качестве точного значения выводимой переменной принимается максимальное значение функции принадлежности.
Слайд 16
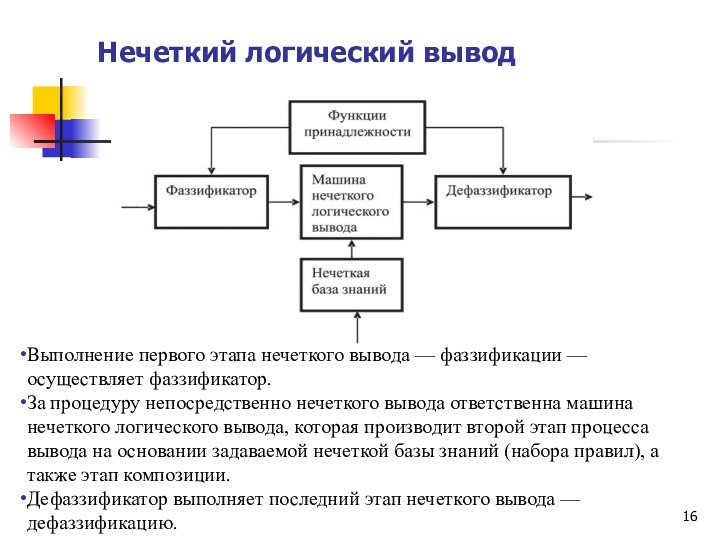
Нечеткий логический вывод
Выполнение первого этапа нечеткого вывода —
фаззификации — осуществляет фаззификатор.
За процедуру непосредственно нечеткого вывода
ответственна машина нечеткого логического вывода, которая производит второй этап процесса вывода на основании задаваемой нечеткой базы знаний (набора правил), а также этап композиции.
Дефаззификатор выполняет последний этап нечеткого вывода — дефаззификацию.
Слайд 17
Методы дефаззификации
В теории нечетких множеств процедура дефаззификации аналогична
нахождению характеристик положения (математического ожидания, моды, медианы) случайных величин
в теории вероятности.
Простейшим способом выполнения процедуры дефаззификации является выбор четкого числа, соответствующего максимуму функции принадлежности.
Однако пригодность этого способа распространяется лишь на одноэкстремальные функции принадлежности.
Для многоэкстремальных функций принадлежности часто используются следующие методы дефаззификации:
Слайд 18
Методы дефаззификации
Для многоэкстремальных функций принадлежности часто используются следующие
методы дефаззификации:
1) COG (Center Of Gravity) — "центр тяжести".
Физическим аналогом этой формулы является нахождение центра тяжести плоской фигуры, ограниченной осями координат и графиком функции принадлежности нечеткого множества.
2) MOM (Mean Of Maximums) — "центр максимумов". При использовании метода центра максимумов требуется найти среднее арифметическое элементов универсального множества, имеющих максимальные степени принадлежностей.
3) First Maximum — "первый максимум" — максимум функции принадлежности с наименьшей абсциссой.
Слайд 19
Следует отметить также тот факт, что с помощью
преобразований нечетких множеств любое правило, содержащее в левой части
как конъюнкции, так и дизъюнкции, можно привести к системе правил, в левой части каждого будут либо только конъюнкции, либо только дизъюнкции. Таким образом, не уменьшая общности, можно рассматривать правила, содержащие в левой части либо только конъюнкции, либо только дизъюнкции.
Каждое из правил представляет из себя нечеткую импликацию. Степень уверенности посылки мы вычислили, а степень уверенности заключения задается функцией принадлежности соответствующего терма. Поэтому, используя один из способов построения нечеткой импликации, мы получим новую нечеткую переменную, соответствующую степени уверенности в значении выходных данных при применении к заданным входным соответствующего правила.