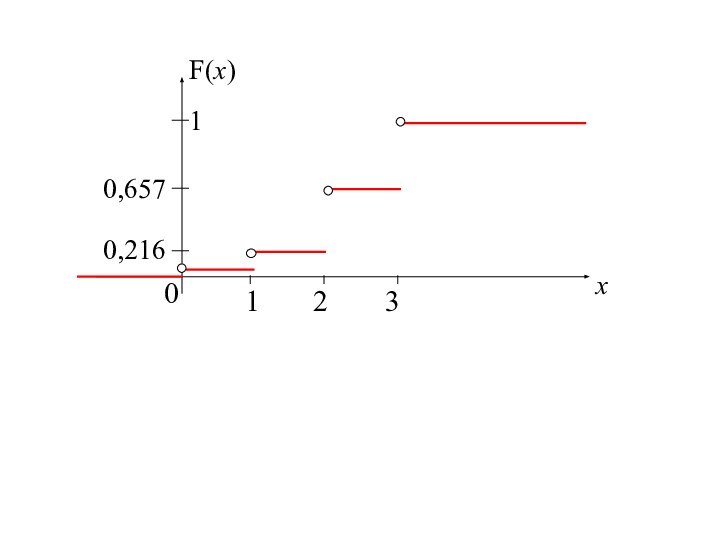
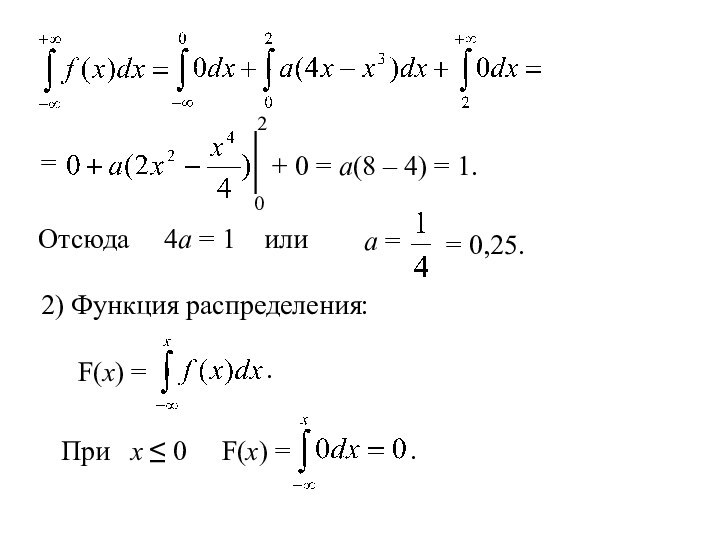распределения) F(x).
2. С помощью дифференциальной функции рас-пределения (или
плотности распределения) f(x).Определение. Функцией распределения СВ Х называется такая функция F(x), которая для лю-
бого числа х определяет вероятность того, что СВ Х примет значения Х < x:
F(x) = P(Х < x).