- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
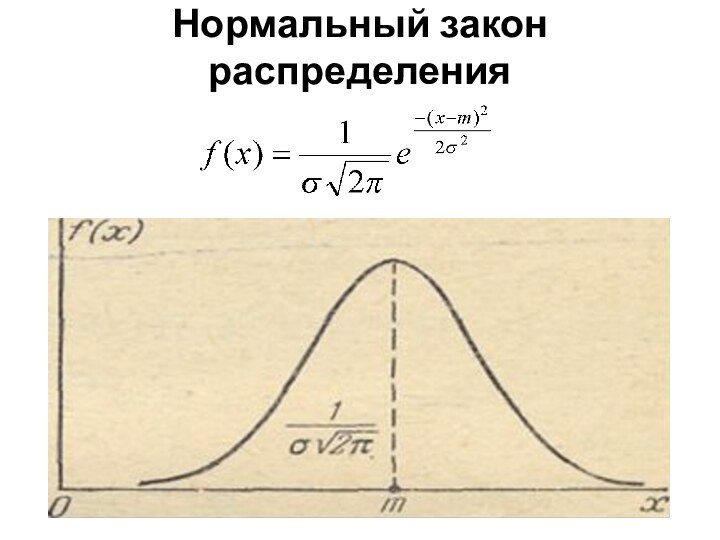
Презентация на тему Нормальный закон распределения
Содержание
- 2. Нормальный закон распределенияМожно доказать, что сумма достаточно
- 3. Нормальный закон распределения
- 4. Нормальный закон распределенияРис. 2.2. Смещение кривой нормального
- 7. Правило «трех сигма» Р (т < X
- 9. Распределение Пуассона Во многих задачах
- 12. Распределение Пуассона. (матожидание)
- 14. Распределение Пуассона.
- 15. Логнормальное распределениеПусть S(t) - цена этой ценной
- 16. Логнормальное распределение Центральная предельная теорема
- 17. Логнормальное распределение Переменная
- 19. Логнормальное распределение.
- 20. Матрицы Матрицей размера m на
- 21. Скачать презентацию
- 22. Похожие презентации
Нормальный закон распределенияМожно доказать, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем















Слайд 4
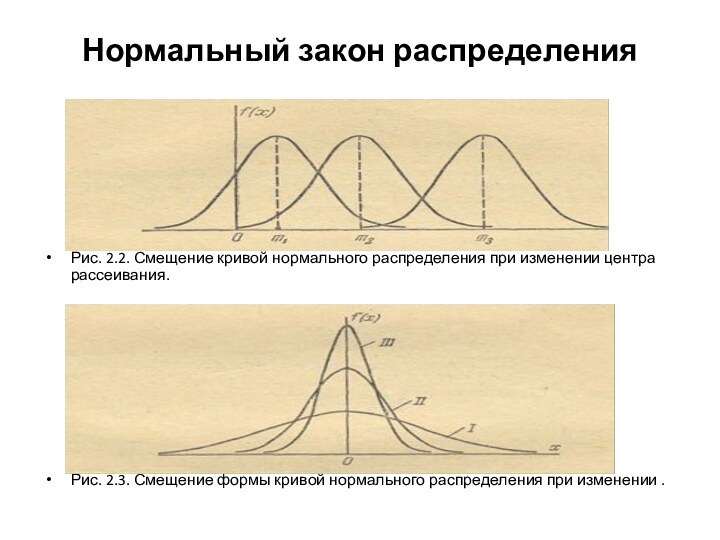
Нормальный закон распределения
Рис. 2.2. Смещение кривой нормального распределения
при изменении центра рассеивания.
Рис. 2.3. Смещение формы кривой нормального
распределения при изменении .Слайд 5 Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный
участок.
Слайд 6 Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный
участок. Как и всякая функция распределения, функция Ф(х) обладает свойствами: 1.
Ф( ) = 0. 2. Ф( ) = 1. 3. Ф(х) - неубывающая функция. Кроме того, из симметричности нормального распределения с параметрами m = 0, = 1 относительно начала координат следует, что
Слайд 7
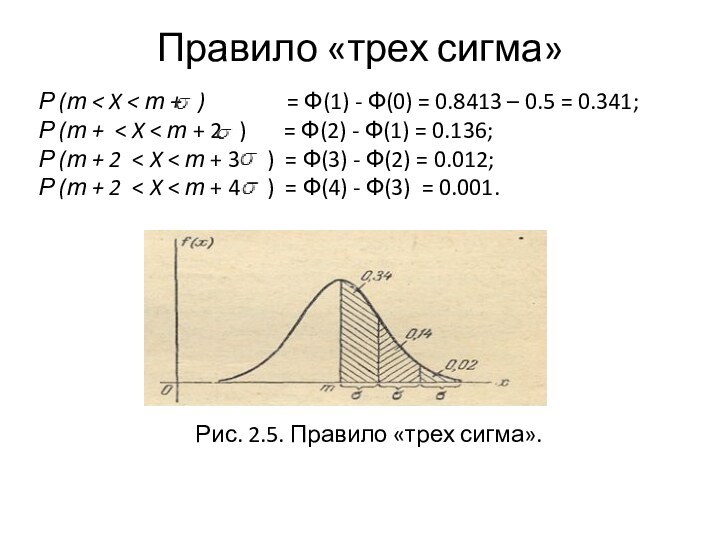
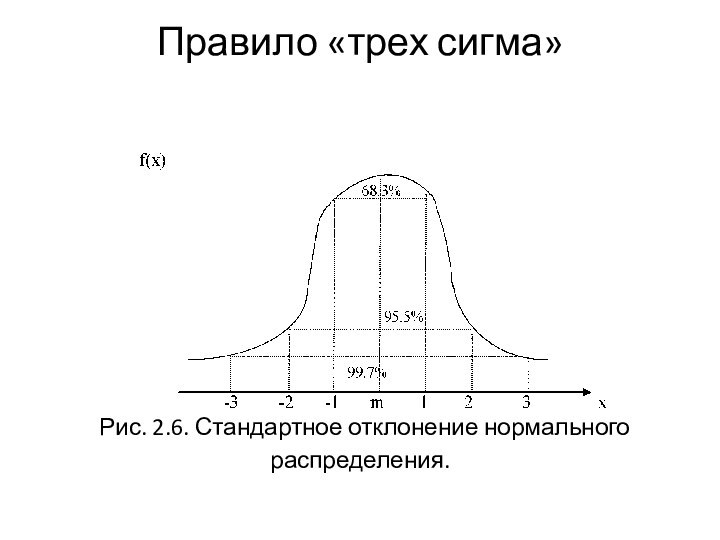
Правило «трех сигма»
Р (т < X
т + )
= Ф(1) - Ф(0) = 0.8413 – 0.5 = 0.341; Р (т + < X < т + 2 ) = Ф(2) - Ф(1) = 0.136; Р (т + 2 < X < т + 3 ) = Ф(3) - Ф(2) = 0.012; Р (т + 2 < X < т + 4 ) = Ф(4) - Ф(3) = 0.001.Рис. 2.5. Правило «трех сигма».
Слайд 9
Распределение Пуассона
Во многих задачах практики
фондового рынка приходится иметь дело со случайными величинами, распределенными
по своеобразному закону; который называется законом Пуассона.Рассмотрим прерывную случайную величину X, которая может принимать только целые, неотрицательные значения: 0, 1, 2, ….m, …. причем последовательность этих значений теоретически не ограничена. Говорят, что случайная величина X распределена по закону Пуассона, если вероятность того, что она примет определенное значение m, выражается формулой:
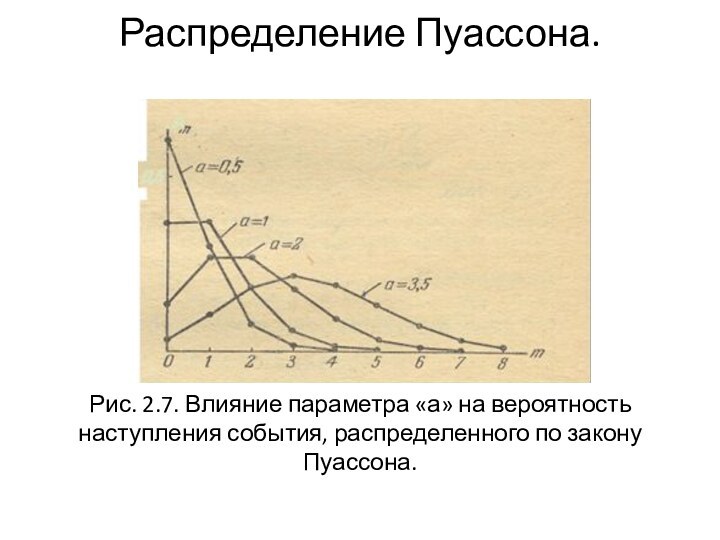
Слайд 11 Распределение Пуассона. Рис. 2.7. Влияние параметра «а» на вероятность
наступления события, распределенного по закону Пуассона.
Слайд 14
Распределение Пуассона.
Таким образом, дисперсия
случайной величины, распределенной по закону Пуассона, равна ее математическому
ожиданию.Это свойство распределения Пуассона часто применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина X распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики (математическое ожидание и дисперсию) случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против гипотезы.
Слайд 15
Логнормальное распределение
Пусть S(t) - цена этой ценной бумаги
в момент времени t и
- цена в момент времени , тогда относительное изменение цены по истечении периода будет равно: .Предположим, что каждое из таких отношений цен на протяжении короткого отрезка времени
было случайной переменной, независимой и идентично распределенной. Тогда согласно центральной предельной теореме величины
- нормально распределены.
Слайд 16
Логнормальное распределение
Центральная предельная теорема гласит,
что если мы рассматриваем большую случайную выборку, то средняя
величина ее будет нормально распределена. Таким образом, когда мы разделяем период времени на большое число промежутков (больше 30), с чем мы имеем дело, когда рассматриваем время как непрерывное, то сумма натуральных логарифмов будет нормально распределена.
Слайд 17
Логнормальное распределение
Переменная называется
логнормально распределенной, если натуральный логарифм ее нормально распределен. Следовательно,
если величинанормально распределена, то величина
должна быть распределена логнормально.
Слайд 18
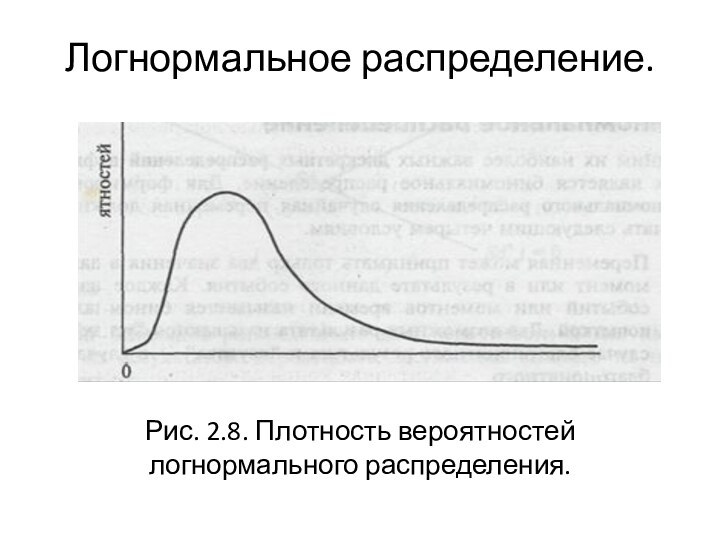
Логнормальное распределение.
Рис. 2.8. Плотность вероятностей логнормального распределения.
Слайд 19
Логнормальное распределение.
Это очень привлекательная
модель распределения отношений цен ценных бумаг, потому что, если
цена растет, то отношение цен будет больше единицы, если падает - то отношение цен будет меньше единицы, но оно никогда не принимает отрицательного значения.На рисунке логнормальное распределение вытянуто вправо, но не имеет отрицательных значений. Это совместимо с возможным распределением цен ценных бумаг, поскольку они не могут упасть ниже нуля, и только очень немногие из наблюдений могли быть очень высоки.
Слайд 20
Матрицы
Матрицей размера m на n
называется прямоугольная таблица чисел, содержащая m строк и n
столбцов. Числа, составляющие матрицу, называются элементами матрицы.Виды матриц. Матрица, состоящая из одной строки, называется вектором-строкой, а из одного столбца – матрицей-столбцом. Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n.





























