- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ОбзорОбобщенная регрессионная модель
Содержание
- 2. Ошибки спецификации модели не включение в модель
- 3. Обозначения вектор-столбец наблюдений зависимой переменной
- 4. Исходя из и
- 5. Сумма квадратов остатков
- 7. Пример Необходимо определить, как товарооборот сети магазинов
- 11. Рассчитаем произведение матриц
- 12. Найдем обратную матрицу
- 13. Рассчитаем .
- 14. Найдем
- 15. Регрессионная модель
- 16. Интерпретация модели при изменении размера торговой площади
- 17. Свойства оценок параметров несмещенность;обоснованность;эффективность;инвариантность.
- 18. Оценки параметров модели будут несмещенными, если
- 20. Так как,
- 21. Учитывая
- 22. Смещение Проверка смещенности
- 23. Выборочная оценка
- 24. Выборочные оценки вектора
- 25. Теорема Гаусса-Маркова функция оценивания по методу 1МНК
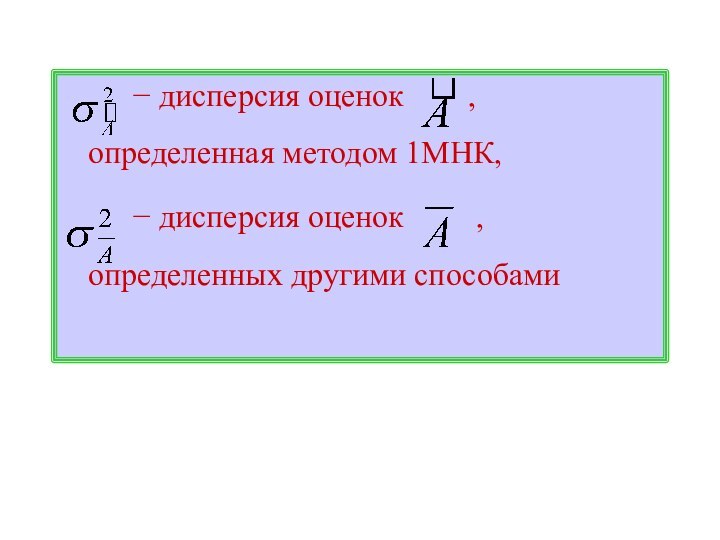
- 26. дисперсия оценок ,
- 27. !!!Функция оценивания 1МНК в классической линейной модели
- 28. Оценка параметров
- 29. Коэффициент множественной детерминации Коэффициент множественной корреляции Выборочная дисперсия Среднеквадратическое отклонение
- 30. Коэффициенты корреляции, детерминации, эластичности
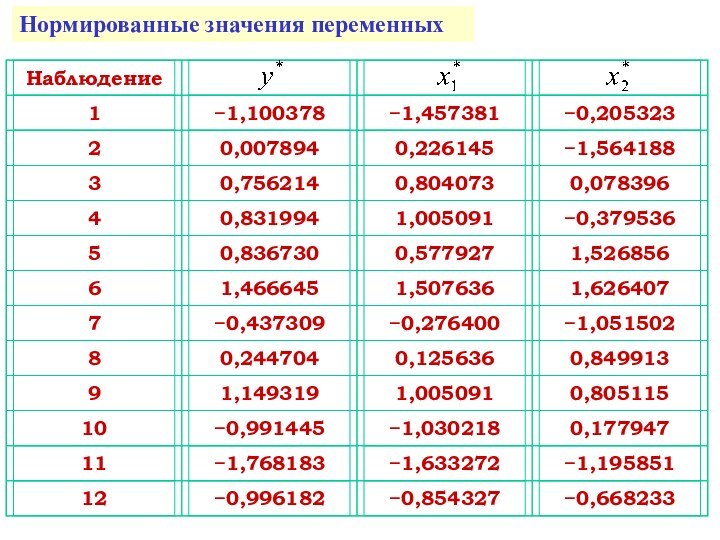
- 31. 1. Нормировка
- 32. 2. Расчет коэффициентов парной корреляции
- 33. Средние и СКО
- 34. Нормировкаи так далее
- 35. Нормированные значения переменных
- 36. Коэффициенты парной корреляции
- 39. Матрица коэффициентов парной корреляции
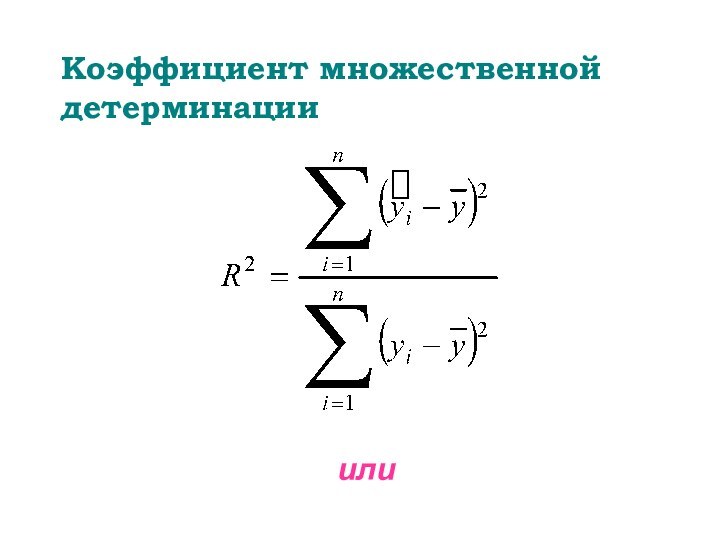
- 40. Коэффициент множественной детерминации или
- 42. Скорректированный коэффициент множественной детерминации (с учетом числа степеней свободы)
- 43. Коэффициент множественной корреляции
- 46. Вариация включенных в модель факторов на 98,585% объясняет вариацию зависимой переменной
- 47. Коэффициент эластичности
- 48. Средние
- 49. Коэффициенты эластичности
- 51. Скачать презентацию
- 52. Похожие презентации
Ошибки спецификации модели не включение в модель существенно влияющего фактора (факторов);включение в модель несущественно влияющего фактора (факторов);использование видов зависимостей, не соответствующих истинной форме связи.




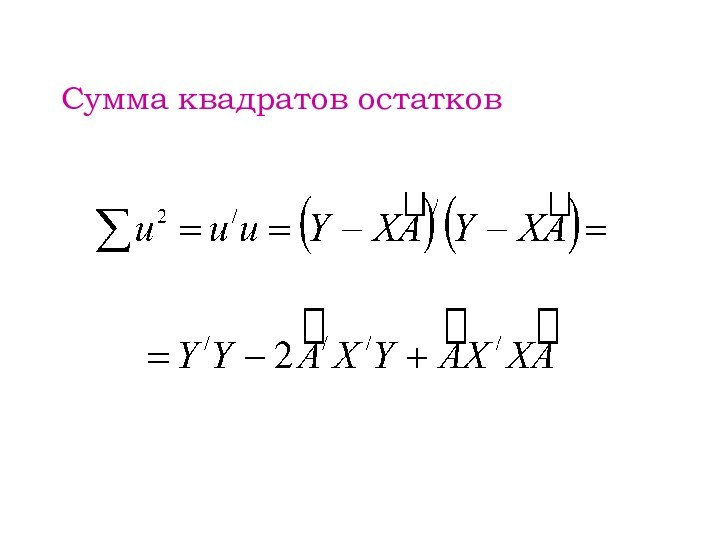
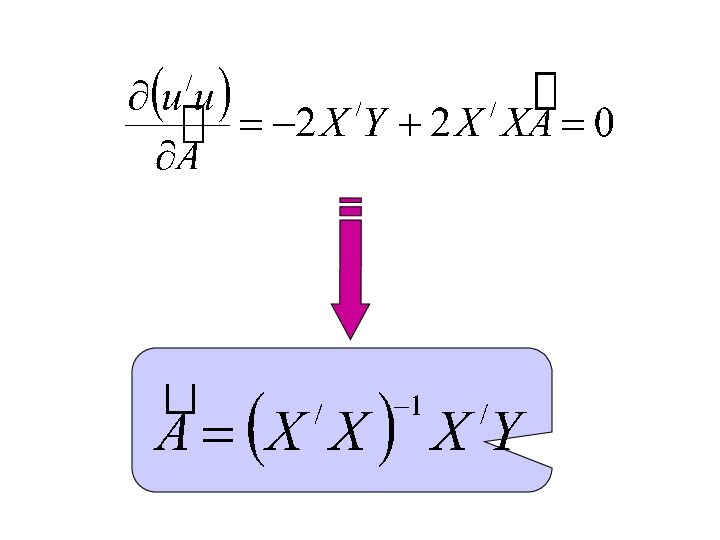










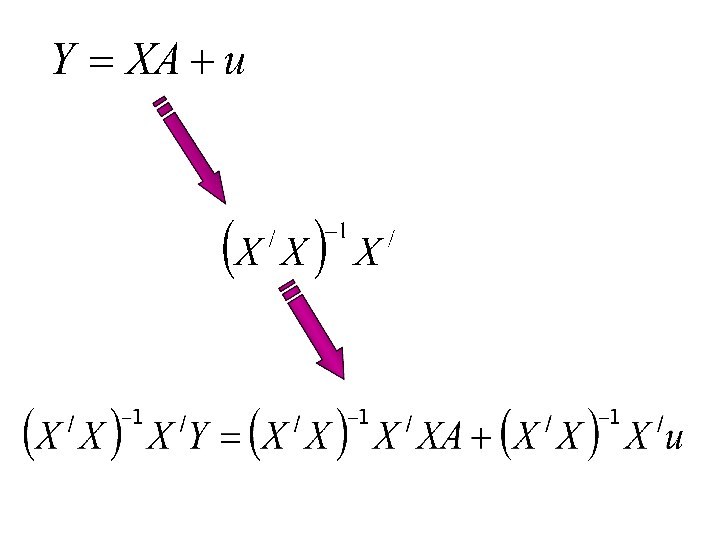
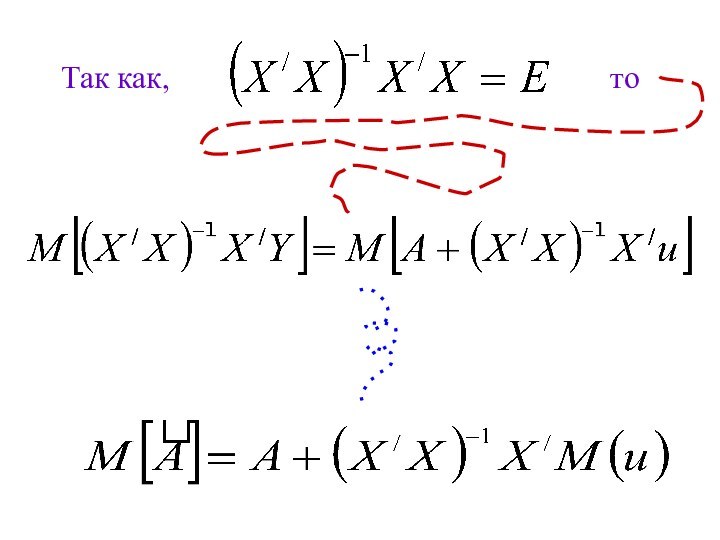




















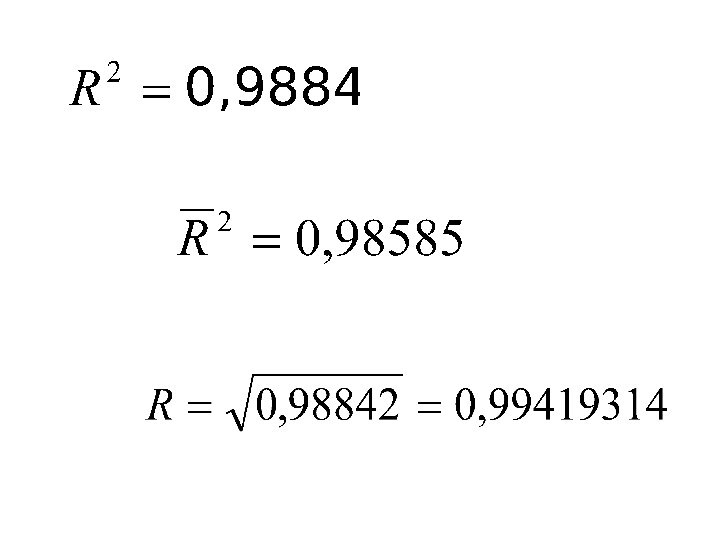


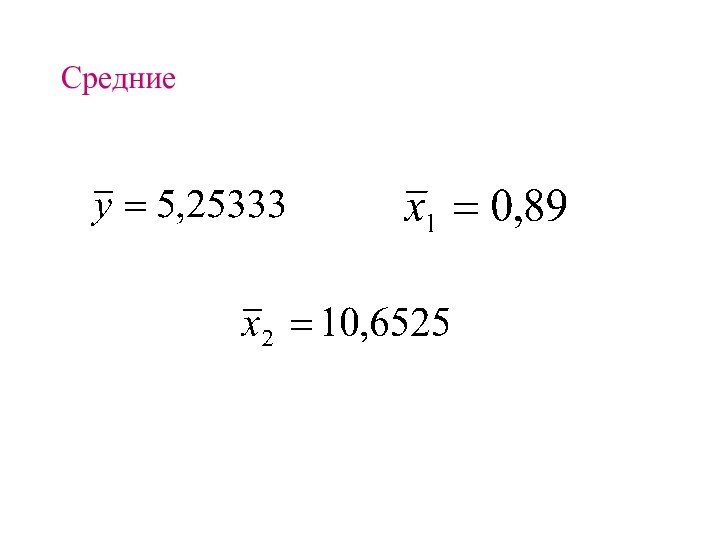



Слайд 2
Ошибки спецификации модели
не включение в модель существенно
влияющего фактора (факторов);
видов зависимостей, не соответствующих истинной форме связи.
Слайд 3
Обозначения
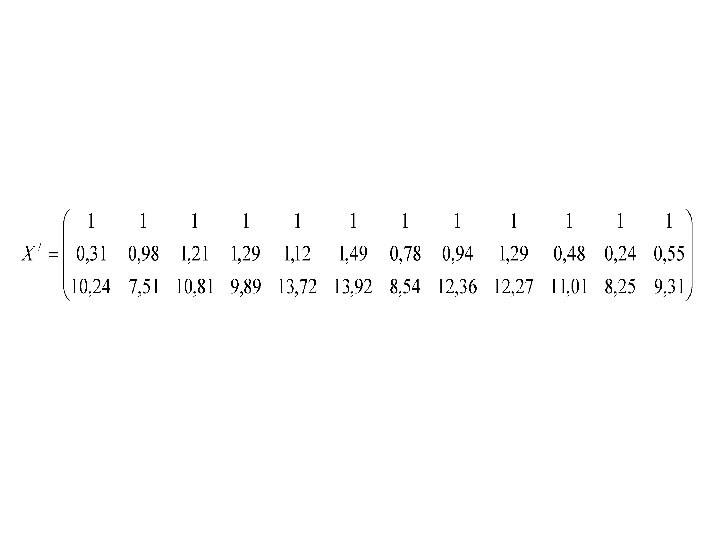
вектор-столбец наблюдений зависимой переменной
матрица наблюдений независимых переменных
вектор-столбец оцениваемых параметров
вектор-столбец
остатков
Слайд 7
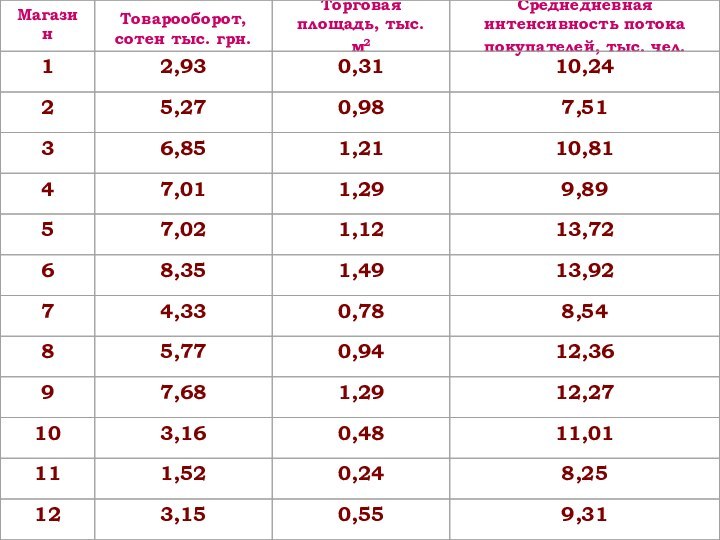
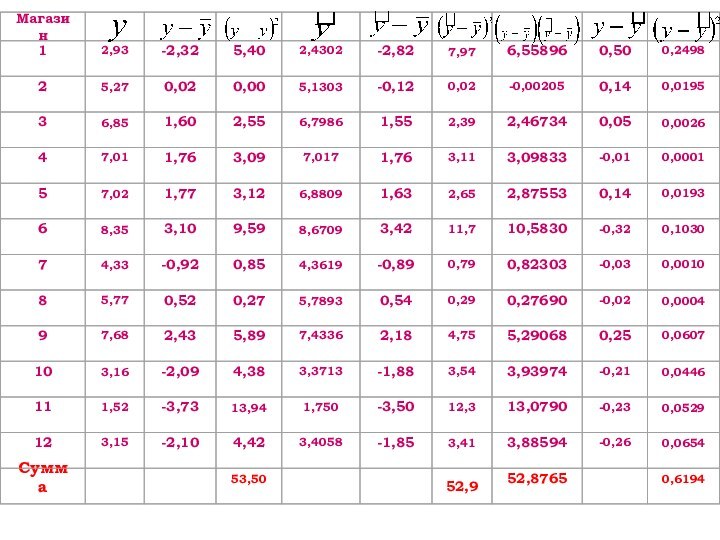
Пример
Необходимо определить, как товарооборот сети магазинов зависит
от их торговой площади и среднедневной интенсивности потока покупателей
Слайд 16
Интерпретация модели
при изменении размера торговой площади на
одну тыс. м2, при прочих равных условиях, товарооборот увеличится
на 4,74 сотен тыс. грн.при увеличении среднедневного потока покупателей на одну тыс. чел., при прочих равных условиях, товарооборот возрастет на 0,175 сотен тыс. грн.
Слайд 18 Оценки параметров модели будут несмещенными, если математическое
ожидание их выборочных значений, найденных при многократном повторении выборки,
не отличается от истинного значения 1
Слайд 23 Выборочная оценка называется
обоснованной, если для любого сколь угодно малого числа
выполняется соотношение 2
Слайд 24 Выборочные оценки вектора будут
только тогда эффективными, когда их дисперсии будут наименьшими
3
Слайд 25
Теорема Гаусса-Маркова
функция оценивания по методу 1МНК покомпонентно
минимизирует дисперсию всех линейных несмещенных функций вектора оценок
Слайд 26 дисперсия оценок , определенная
методом 1МНК,
дисперсия оценок
, определенных другими способами
Слайд 27
!!!
Функция оценивания 1МНК в классической линейной модели является
лучшей линейно несмещенной функцией оценивания
(с англ. BLUE
Best Linear Unbiased Estimator) Слайд 28 Оценка параметров
называется инвариантной, если для произвольно заданной функции
оценка параметров функции представляется в виде 4





























