Презентация на тему Оптическая модель упругого рассеяния

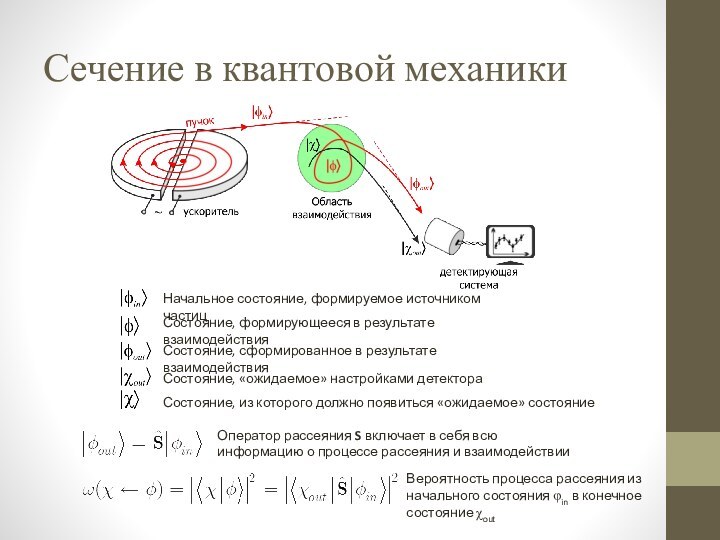
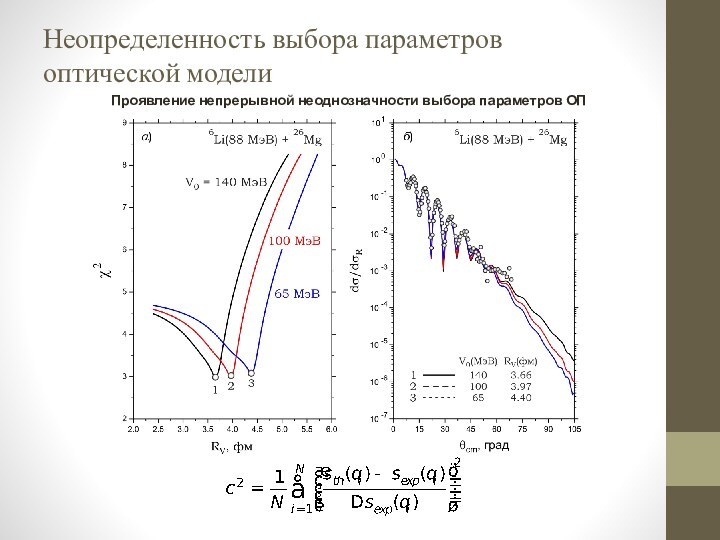
формирующееся в результате взаимодействия
Состояние, сформированное в результате взаимодействия
Состояние, «ожидаемое»

настройками детектора

Оператор рассеяния S включает в себя всю информацию о процессе рассеяния и взаимодействии

Состояние, из которого должно появиться «ожидаемое» состояние

Вероятность процесса рассеяния из начального состояния fin в конечное состояние cout

разложение по плоским волнам)
Содержит информацию о рассеянии
Нет рассеяния
Вероятность

того, что в конечном состоянии система имеет импульс p

Вероятность рассеяния в телесный угол Wp в направлении импульса p

что здесь каждое суммируемое состояние (событие) до столкновения есть

копия начального состояния, смещенного в перпендикулярной плоскости на некоторый прицельный параметр r

Сечение рассеяния (угловое распределение рассеянных частиц):

Таким образом, знание амплитуды рассеяния позволяет определить сечение.

, то мы можем вычислить

и сечение рассеяния.

Как вычислить амплитуду рассеяния?

Амплитуда рассеяния связана с матричными элементами T оператора (см. подробно книгу Дж. Тейлора, Квантовая теория рассеяния):

здесь V – это оператор взаимодействия, а вектор – это, так называемое, стационарное состояние рассеяния, соответствующее истинному состоянию, реализующемуся из начальной плоской волны .

решение интегрального уравнения Липпмана-Швингера (так никто не делает!)
В координатной

форме это уравнение имеет вид:

Отметим, что асимптотика волновой функции имеет вид

Падающая плоская волна

Расходящаяся (или сходящаяся) сферическая волна

Амплитуда рассеяния

состояние является собственным
Решение удобно искать используя парциальное разложение в.ф.
Парциальные

волновые функции имеют асимптотику знакомого вида:

где появляются парциальные амплитуды, связанные с амплитудой рассеяния

Таким образом, для нахождения амплитуды рассеяния в данном случае достаточно найти ограниченный набор парциальных амплитуд (заметим, что начиная с некоторого l фазы рассеяния dl = 0, а значит вклад этих слагаемых в амплитуду равен нулю). Сделать это можно выполнив численное решение парциальных уравнений Шрёдингера.

Парциальная амплитуда

уравнение Шрёдингера, использования свойств ортогональности сферических гармоник, получим набор

радиальный уравнений

дополненных граничными условиями

Область численного решения

Область асимптотического решения

«Сшивка» численного и асимптотического решения в точке Rm дает возможность получить значения парциальных амплитуд.

исключительно упругой компонентой полной волновой функции. Тогда введем проекционный

оператор, выделяющий именно упругую компоненту

Очевидно, что оператор будет выделять – оставшуюся часть в.ф., содержащую информацию обо всех неупругих каналах.

Это и есть обобщенный оптический потенциал!

можно свести к полностью одноканальной задаче!

Платой за такое упрощение

служит исключительная сложность расчета оптического потенциала. Его вычисление эквивалентно решению исходной многоканальной задачи!

Однако, самое важное следствие теории Фешбаха состоит в том, что оптический потенциал существует в принципе!

+ b, при этом частица a имеет внутреннюю структуру,

а именно два возможных состояния. Гамильтониан такой системы можно записать в виде


Проекционные операторы можно определить как


Действие этих операторов совместно с гамильтонианом



где

и тогда оптический потенциал принимает вид

Оператор Грина – пропогатор

Оптический потенциал нелокальный, комплексный и зависит от энергии

попытки подобрать его в простой для применения форме. Наиболее

часто на практике применяют оптический потенциал в виде суммы нескольких слагаемых

Радиальная зависимость каждого из них (кроме кулоновского) имеет вид функции Вудса-Саксона



Параметры потенциала подбираются так, чтобы описать имеющиеся эксперимен-тальные данные по упругому рассеянию атомных ядер.

Для некоторых ядер-снарядов оказалось возможным подобрать параметры в виде аналитических функции энергии и массы мишени, получая при этом хорошее согласие с данным в широком диапазоне масс и энергий столкновения!

scattering of 6,7Li projectiles, Nuclear Physics A388 (1982)153

нескольких глобальных оптических нуклон-ядерных потенциалов:
1. LOCAL AND GLOBAL NUCLEON

OPTICAL MODELS FROM 1 keV TO 200 MeV, A.J. Koning, J.P. Delaroche, Nuclear Physics A713(2003) 231–310
2. A GLOBAL NUCLEON OPTICAL MODEL POTENTIAL, R.L. VARNER, W.J. THOMPSON, T.L. McABEE, E.J. LUDWIG and T.B. CLEGG, Phys. Rep. 201 (1991) 57-119
3. NUCLEON-NUCLEUS OPTICAL-MODEL POTENTIAL, A > 40, E > 50 MeV, F.D. Becchetti, G.W. Greenlees, Phys. Rev. 182 (1969) p.1190
4. Также можно выполнить автоматическую подгонку параметров потенциала

параметров ОП

параметров ОП для реакции 6Li(13 МэВ) + 12C
дискретная
непрерывная

-166.9 МэВ
V0 = -125.3 МэВ
Два потенциала взаимодействия с разной

геометрией могут приводить к одинаковому (или близкому) набору фаз рассеяния, а значит одинаковому сечению рассеяния! Отличие волновых функций состоит только в количестве нулей (т.е. связанных состояний) в области взаимодействия.

Асимптотика волновой функции и амплитуда рассеяния

Кулоновская в.ф.