Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Опционные модели

Содержание

Опционы — это ценные бумаги, дающие инвестору право купить или продать другие ценные бумаги или иные активы по специально оговоренной цене в течение определенного срока.… рынок ценных бумаг…
Опционные модели Опционы — это ценные бумаги, дающие инвестору право купить или продать другие …к управлению активами: Основные понятия Основные понятия Права и обязательства сторон опционного контрактаОпцион коллОпцион пут ПокупательколлПродавецколлПродавецпутПокупательпутимеетимеетимеетимеетПраво напокупкуОбязанностьпродажиПраво напродажуОбязанностьпокупкиОпределенного товарапо Существуют два вида опционов: СALL- право купить по фиксированной цене а)варранты на Операции в колл-опционе Денежные выплаты, получаемые владельцем опциона (по опциону с правом покупки только в Временная стоимостьЧасть премии, на которую она превосходит внутреннюю стоимость, называется временной стоимостью.Временная Моделирование цены колл, пут-колл паритетЦена колл является внутренней оценкой опциона, как производного Доходность проекта можно представить следующей диаграммой (call) : ….Реальный опционТермин «реальный опцион» первым предложил использовать Стюарт Майерс. Он рассматривал будущие Опционный подход к инвестиционным проектам опцион на продажу активов по Опцион на продажу активов по проекту (или перепрофилирование активов на производство другой Опцион на отсрочку инвестиционных затрат При рассмотрении проектов возникает несколько вопросов: 1) Опцион на будущие проекты При рассмотрении инвестиционного проекта базовое значение NPV должно Факторы, влияющие на оценку финансовых и реальных опционов Область применения реальных опционов Применение методики реальных опционов к оценке инвестиционных проектов Применение реальных опционов в оценке инноваций Следующие характеристики инновационных проектов обуславливают необходимость Типы реальных опционов Типы реальных опционов Типы реальных опционов Методы оценки опционов Сравнение традиционного взгляда и перспективы реальных опционов Формула ценности проекта или компании в условиях неопределенности:Истинная ценность = Ожидаемое NPV+Ценность реальных опционов Методы оценки стоимости реального опциона При определении стоимости реальныхопционов используются следующие методы: Биномиальная модель оценки колл опционаБиномиальная модель (binomial model) оценки Допущения биномиальной модели Техника построения Биномиальная модель Дерево решений трехступенчатой биномиальной модели (S- первоначальная стоимость актива, Биномиальная модель Кокса, Росса, Рубинштейна ПрименениеТеоретически: оценка премий любых опционовПрактически: оценка премий американских опционовАкцииФьючерсыВалютаОценка величины премии, двигаясь Технология.Шаг 1. Разбиение всего периода действия контракта на интервалы.Шаг Обозначения и формулы (для опционов на акции)u – процент прироста стоимости Обозначения и формулыП – премия опциона Проверка на исключение арбитража: ПоправкиДля опционов на фьючерсыДля опционов на валюту Пример для бездивидендной акции УсловияПокупка трехмесячного опциона пут на акцииКурс акции в момент заключения S=40Цена исполнения РешениеΔt=1/12=0.8(3) 1-p=0.4837 Прогноз курса акции Su=S*u=40*1.1063=44.25 Sd=S*d=40*0.9039=36.16Расчет премии Su2: Модификация для акций, по которым выплачиваются дивидендыДивиденд в виде процента – ставка дивиденда q Модификация для акций, по которым выплачиваются дивидендыДивиденд в абсолютном выражении Пример для опциона на акции, по которым выплачивается дивиденд в абсолютном выражении УсловияПокупка опциона пут на четыре месяцаТекущий курс акции 48Цена исполнения Ци=45Стандартное отклонение РешениеПриведенная стоимость дивиденда к текущему моменту 3*e-0.1*0.25=2.93 (0.25 – 3/12 года)Чистая Su: чистая цена=45.07*1.1063=49.86 привед. Д=3*e-0.1*0.1667=2.95 (0.1667 – 2/12 года) Простая биномиальная модель оценки премии опционов Простая биномиальная модель оценки премии опциона значение опциона и курса акций рассматривается только Простая биномиальная модель оценки премии европейского опциона callТ0: t – количество месяцев; Момент Т1если P1asset(T1)Pstrikе, π = Passet - Pstrike Портфель без рискаПортфель: покупка n акций и продажа 1опционаПортфель без риска, Vportfolio:n*P1asset(T1) Стоимость портфеляТ0:Passet(T0)*n – π= Vportfolio*e-i*t/12π = Passet(T0)*n – Vportfolio*e-i*t/12 Числовой примеревропейский опцион callt=5 месPasset(T0)=$33;Pstrike=$36; i=10%; P1asset(T1) = 34; P2asset(T1) = 38? Недостатки моделиНе введен элемент вероятностной оценкиОграничивается только двумя конечными значениями актива Уравнение однопериодной биноминальной модели ценообразования европейских опционов put на акции , не При построении «дерева решений» с большим Модель Блэка - Шоулза Модель Блэка - ШоулзаФормула модели оценки опционов впервые была выведена Фишером Блэком Модель Блэка-Шоулзаhttp://www.optionline.ru/optionCalculator/ Модель Блэка-Шоулза (обозначения)C(S,t) - текущая стоимость опциона call в момент t до Модель Блэка-Шоулза (для проектов)где NPV1 – чистая дисконтированная стоимость проекта 1; Сор Факторы, определяющие стоимость опционаВнутренняя стоимостьТекущая цена актива на физическом рынке, цена спотЦена Влияние факторов на премию опциона При построении модели Блэк и Шоулз исходили из следующих условий: Волатильность (Implied Volatility) Волатильность бывает двух видов: подразумеваемая (ожидаемая) волатильность (IV Применение волатильностиулыбкаухмылка- волатильность тем выше, чем дальше страйк от текущей цены- «улыбка» Греки – это опционные характеристики, описывающие чувствительность цены опциона к переменным моделиDelta ГрекиТета представляет собой первую частную производную формулы Блэка-Шоулса по параметру времени до Греки. Покупка опциона Call Интересные особенности ценообразования для европейского опциона «колл».Можно показать, что произойдет с действительной Выигрыши и потери при различных стратегиях Оценка портфеля опционов Оценка портфеля опционов 5. Опционный подход Реальные опционы и инвестиции фирмыРеальный опцион – право менеджмента принять решениеПраво менеджера Входные параметры Правила принятия решений Методология оценкиФормирование портфеля-копии (дублирующего будущие денежные потоки) с использованием:Базового актива (акции для Методология оценки Методология оценки Методология оценки Методология оценки Оценка опциона на ликвидациюВ компании реализуется инвестиционный проект, NPV которого равна $100. Оценка опциона на ликвидациюИзначально, стоимость опциона на ликвидацию можновычислить только на момент Оценка опциона на ликвидациюТаким образом, в конце первого периода в случае уменьшении Оценка опциона на ликвидацию Рискнейтральный подход к оценке Рискнейтральный подход к оценке Особенности оценки портфеля реальных опционов Особенности метода реальных опционов Преимущества и недостатки метода реальных опционов Преимущества дает более объективную и многостороннюю С точки зрения оценки бизнеса нас интересуют следующие типы опционов: Примеры Расчет Пример 2. Опцион на отказ.Технология А предусматривает использование заказного оборудования, управляемого с Пример 3.Опцион на выбор времени.Текущая стоимость = $ 200 млн. В случае Пример 4Предположим, что компания рассматривает проект стоимостью $ 4 млн и его Отдача: 2 варианта$ 6,6 млн.Текущая стоимость=$ 4,5 млн.$ 3,3 млн.R=10% DCF$ 4,5 млн. - $ 4 млн. = $ 500 тыс.Проект можно запускать Решение с помощью метода реальных опционовИспользуем биномиальную модель опционного ценообразования.Допустим, безрисковая ставка Варианты действийСохранение опционаРеализация опционаNPV=$ 0,8225 млн.NPV=$ 0,5 млн. Бизнес-решения, принятые на основе теории реальных опционовслияние Time Warner и AOL с Появление метода реальных опционов — это важный шаг в развитии анализа эффективности. ОПЦИОНЫ: описание, графики, калькуляцияhttp://www.optiondesk.ru/?code=informationhttp://optiontraders.ru/2008/04/29/vertikalnye-spredy/ Калькуляция стоимости сложных опционовНа практике чаще всего встречаются весьма сложные реальные опционы. Паритет опционов на покупку и продажуСуществует хорошо известная зависимость между стоимостью колл Стоимость опциона на покупку + текущее значение цены исполнения = стоимость опциона Покупка опциона кол л. Long Call. Прямое создание Лонг Колл А Покупка опциона пут. Long Put. Прямое создание Лонг Пут А Описание Самая Продажа опциона колл. Short Call. Описание Одна из самых простых стратегий. Однако Продажа опциона пут. Short Put. Описание Одна из самых простых стратегий. Однако ВведениеОпцион – срочный контракт, дающий право, но не обязанность купить/продать базовый актив ОпределенияОпцион call - дает право, но не обязанность купить базовый актив по Направленные позиции«Бычья» позиция: Покупка опционов call Продажа опционов putПокупка call-спредаПродажа put-спреда Цена на момент исполнения«Бычья» позиция Покупка опциона call дает возможность заработать на повышательном Цена на момент исполнения Покупка call- спреда – покупка ATM или ITM опциона Направленные позиции«Медвежья» позиция:Покупка опционов putПродажа опционов call Покупка put-спредаПродажа call-спреда Цена на момент исполнения«Медвежья» позиция Покупка опциона put – дает возможность заработать на Цена на момент исполнения Покупка put-спреда – покупка ATM или ITM опциона put Cтратегии покупки/продажи волатильности Стредл (straddle) Стренгл (strangle) Цена на момент исполнения Стредл – одновременная покупка опционов put и call с Цена на момент исполненияПродажа Стредла и СтренглаP&LПродажа стредлаПродажа стренгла Продажа стредла и стренгла Опционная стратегия с удержанием базового активаZero-premium collarPut-spread collarПокрытая продажа опциона Цена на момент исполненияZero-premium collar Zero-premium collar – хеджирование позиции в базовом активе Put-spread collarPut-spread collar можно создать объединив Collar с put-спредом. Подобная комбинация создает Цена на момент исполненияПокрытая продажа опционаПокрытая продажа опциона – позиция в базовом
Слайды презентации

Слайд 2 Опционы — это ценные бумаги, дающие инвестору право

Опционы — это ценные бумаги, дающие инвестору право купить или продать

купить или продать другие ценные бумаги или иные активы

по специально оговоренной цене в течение определенного срока.

… рынок ценных бумаг…

Слайд 3 …к управлению активами: Основные понятия

…к управлению активами: Основные понятия

Слайд 4 Основные понятия

Основные понятия

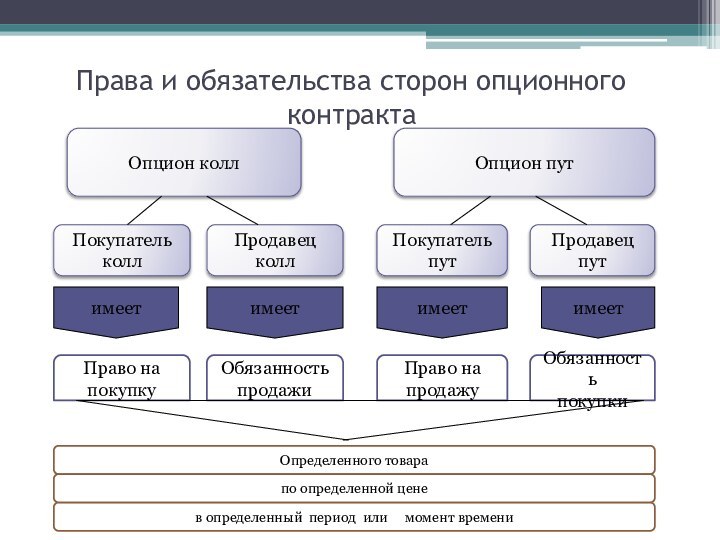
Слайд 5 Права и обязательства сторон опционного контракта
Опцион колл
Опцион пут

Права и обязательства сторон опционного контрактаОпцион коллОпцион пут ПокупательколлПродавецколлПродавецпутПокупательпутимеетимеетимеетимеетПраво напокупкуОбязанностьпродажиПраво напродажуОбязанностьпокупкиОпределенного


Покупатель
колл
Продавец
колл
Продавец
пут
Покупатель
пут
имеет
имеет
имеет
имеет
Право на
покупку
Обязанность
продажи
Право на
продажу
Обязанность
покупки
Определенного товара
по определенной цене
в определенный период или

момент времени

Слайд 6 Существуют два вида опционов:
СALL- право купить по

Существуют два вида опционов: СALL- право купить по фиксированной цене а)варранты

фиксированной цене
а)варранты на покупку акций инновационных предприятий, предоставляемые

менеджерам ;
б)опционы на приобретение патентных лицензий

PUT- право продать по фиксированной цене

В зависимости от времени исполнения (реализации права на покупку / продажу) опционы делятся: 1) американский - можно исполнить в любой момент до истечении срока действия 2)европейский - можно исполнить только в день истечения срока действия

Слайд 7 Операции в колл-опционе

Операции в колл-опционе

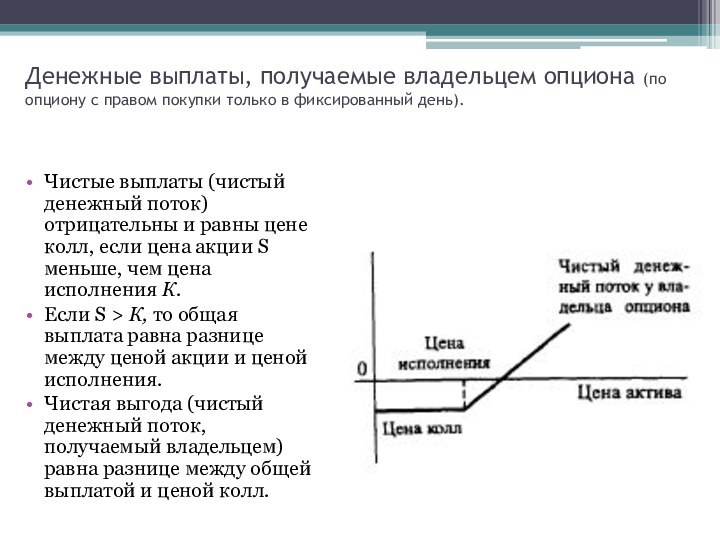
Слайд 8 Денежные выплаты, получаемые владельцем опциона (по опциону с

Денежные выплаты, получаемые владельцем опциона (по опциону с правом покупки только

правом покупки только в фиксированный день).
Чистые выплаты (чистый денежный

поток) отрицательны и равны цене колл, если цена акции S меньше, чем цена исполнения К.
Если S > К, то общая выплата равна разнице между ценой акции и ценой исполнения.
Чистая выгода (чистый денежный поток, получаемый владельцем) равна разнице между общей выплатой и ценой колл.

Слайд 9 Временная стоимость
Часть премии, на которую она превосходит внутреннюю

Временная стоимостьЧасть премии, на которую она превосходит внутреннюю стоимость, называется временной

стоимость, называется временной стоимостью.

Временная стоимость зависит от трех важнейших

факторов, которыми являются следующие:

1. Соотношение страйковой и рыночной цен.

2. Время до истечения срока действия.

3. Волатильность — показатель изменчивости цен.

Слайд 10 Моделирование цены колл, пут-колл паритет
Цена колл является внутренней

Моделирование цены колл, пут-колл паритетЦена колл является внутренней оценкой опциона, как

оценкой опциона, как производного актива, и определяется рядом факторов,

отражающих изменчивость исходного актива и характеристики самого опциона. В общем случае три основных фактора влияют на цену опциона:

характеристики исходного актива;

характеристики прав, гарантируемых опционом;

характеристики финансового рынка.

Слайд 11 Доходность проекта можно представить следующей диаграммой (call) :

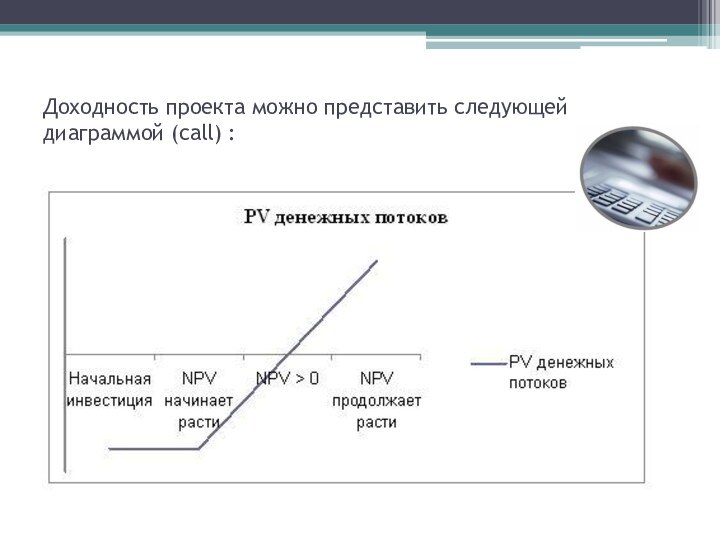
Доходность проекта можно представить следующей диаграммой (call) :

Слайд 12 ….Реальный опцион
Термин «реальный опцион» первым предложил использовать Стюарт

….Реальный опционТермин «реальный опцион» первым предложил использовать Стюарт Майерс. Он рассматривал

Майерс.
Он рассматривал будущие инвестиции предприятия в качестве реальных

опционов и ассоциировал их с возможностями корпоративного роста.
Автор заметил, что стоимость компании отражает ожидания будущих инвестиций, которые являются дискретными величинами по своей природе, и их величина зависит от чистой приведенной стоимости возможностей, появляющихся в будущем.

Слайд 13 Опционный подход к инвестиционным проектам
опцион на продажу

Опционный подход к инвестиционным проектам опцион на продажу активов по проекту

активов по проекту (по сути опцион на отказ от

инвестиционного проекта) — abandonment option;
опцион на отсрочку инвестиционного проекта (возможность отложить затраты по покупке или созданию реальных активов) — timing option;
опцион на новые инвестиционные возможности (strategic investment option)

Слайд 14 Опцион на продажу активов по проекту (или перепрофилирование

Опцион на продажу активов по проекту (или перепрофилирование активов на производство

активов на производство другой продукции) :
Цена опциона (value

of option) =
Оценка проекта с учетом возможности продажи активов
— Оценка проекта без возможности продажи (считая, что инвестиционные затраты необратимы) =
= NPVс опционом — NPV необратимых затрат.

Слайд 15 Опцион на отсрочку инвестиционных затрат
При рассмотрении проектов

Опцион на отсрочку инвестиционных затрат При рассмотрении проектов возникает несколько вопросов:

возникает несколько вопросов:
1) имеется ли опцион на отсрочку

и каково "истинное" значение NPV проекта;
2) какова оценка этого опциона и (более практический вопрос) сколько может стоить право на отсрочку.
Цена опциона = NPV проекта с учетом отсрочки — NPVпроекта, принимаемого немедленно.

Слайд 16 Опцион на будущие проекты
При рассмотрении инвестиционного проекта

Опцион на будущие проекты При рассмотрении инвестиционного проекта базовое значение NPV

базовое значение NPV должно быть скорректировано на чистый дисконтированный

доход, порождаемый различными возможностями.
NPV скорректированное = NPVбазовое + NPV опциона на прекращение + + NPVопциона на следующие проекты + NPVопциона на отсрочку.

Слайд 17 Факторы, влияющие на оценку финансовых и реальных опционов

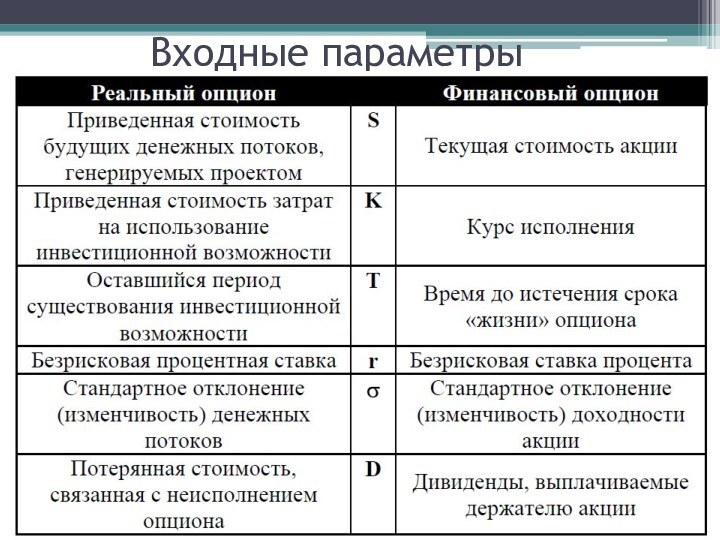
Факторы, влияющие на оценку финансовых и реальных опционов

Слайд 18 Область применения реальных опционов Применение методики реальных опционов к

Область применения реальных опционов Применение методики реальных опционов к оценке инвестиционных

оценке инвестиционных проектов целесообразно, когда выполняются следующие условия:

1)результат проекта подвержен высокой степени неопределенности; 2)менеджмент компании способен принимать гибкие управленческие решения при появлении новых данных по проекту; 3)финансовый результат проекта во многом зависит от принимаемых менеджерами решений. При оценке проекта по методу дисконтированных денежных потоков значения NPV отрицательно или чуть больше нуля .

Слайд 19 Применение реальных опционов в оценке инноваций
Следующие характеристики инновационных

Применение реальных опционов в оценке инноваций Следующие характеристики инновационных проектов обуславливают

проектов обуславливают необходимость применения метода опционной оценки для инвестиционного

анализа:
трудность с адекватной оценкой критерия NPV стандартными подходами (например, при получаемом нулевом значении);
высокая вероятность изменения факторов внешней среды и условий реализации проекта или получения новой информации;
гибкость в управлении и доступ к активным действиям по урегулированию процесса осуществления проекта.

Слайд 20 Типы реальных опционов

Типы реальных опционов

Слайд 21 Типы реальных опционов

Типы реальных опционов

Слайд 22 Типы реальных опционов

Типы реальных опционов

Слайд 23 Методы оценки опционов

Методы оценки опционов

Слайд 24 Сравнение традиционного взгляда и перспективы реальных опционов

Сравнение традиционного взгляда и перспективы реальных опционов

Слайд 25 Формула ценности проекта или компании в условиях неопределенности:

Истинная

Формула ценности проекта или компании в условиях неопределенности:Истинная ценность = Ожидаемое NPV+Ценность реальных опционов

ценность = Ожидаемое NPV+Ценность реальных опционов

Слайд 26 Методы оценки стоимости реального опциона
При определении стоимости

Методы оценки стоимости реального опциона При определении стоимости реальныхопционов используются следующие

реальных
опционов используются следующие методы:

модель оценки стоимости опционов Блэка—Шоулза;


модель оценки стоимости опционов на основе экономической прибыли;
биномиальная модель.

Слайд 27 Биномиальная модель оценки колл опциона
Биномиальная модель (binomial model)

Биномиальная модель оценки колл опционаБиномиальная модель (binomial model) оценки

оценки "истинной", или внутренней (теоретической), цены опциона в текущий

момент (t = 0) строится на простейшем допущении о поведении цены исходного актива.
Или модель Кокса — Росса — Рубинштейна (Сох — Ross —Rubinstein).

Цена колл (оценка опциона) = Текущая цена актива х Количество активов — Привлечение денежных средств для покупки активов = S х R — В.

Предпосылки: известны дискретные значения будущей цены акции; известны вероятностные распределения движения цены.

Слайд 28 Допущения биномиальной модели

Допущения биномиальной модели Техника построения биномиальной позволяет получить

Техника построения биномиальной позволяет получить более точные результаты, когда

существует несколько источников неопределенности или большое количество дат принятия решения. В основе модели лежат два допущения: 1)в одном интервале времени могут быть только два варианта развития событий (худший и лучший); 2)инвесторы нейтрально относятся к риску. Вычисление стоимости опциона данным методом, по сути, представляет собой движение по «дереву решений»

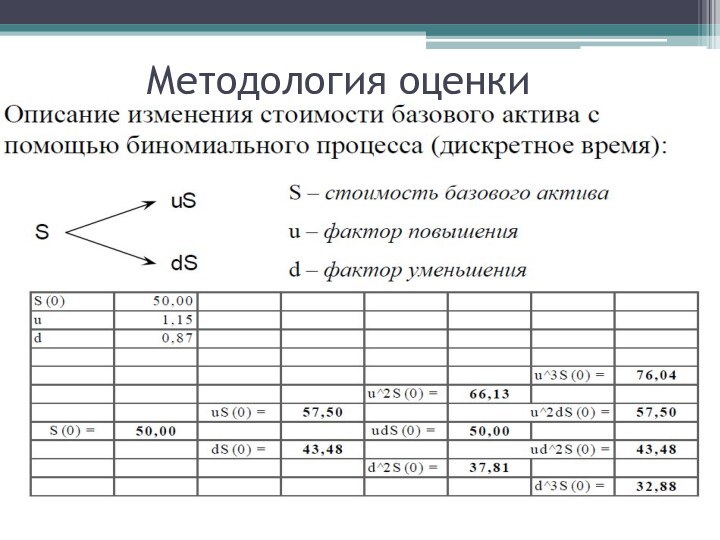
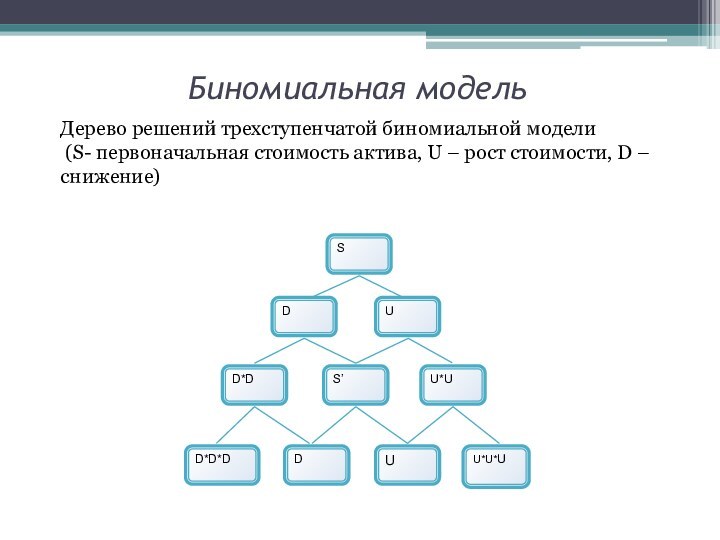
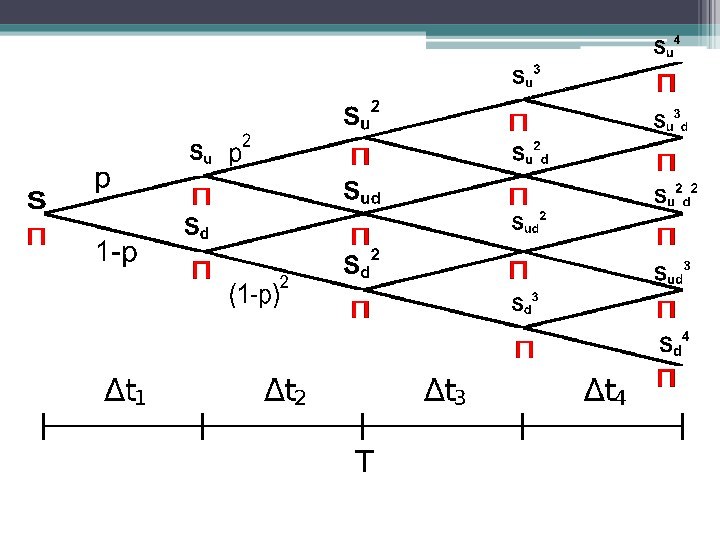
Слайд 29 Биномиальная модель
Дерево решений трехступенчатой биномиальной модели (S-

Биномиальная модель Дерево решений трехступенчатой биномиальной модели (S- первоначальная стоимость актива,

первоначальная стоимость актива, U – рост стоимости, D –снижение)

Слайд 30 Биномиальная модель Кокса, Росса, Рубинштейна

Биномиальная модель Кокса, Росса, Рубинштейна

Слайд 31 Применение
Теоретически: оценка премий любых опционов
Практически: оценка премий американских

ПрименениеТеоретически: оценка премий любых опционовПрактически: оценка премий американских опционовАкцииФьючерсыВалютаОценка величины премии,

опционов
Акции
Фьючерсы
Валюта

Оценка величины премии, двигаясь от дня исполнения в обратном

направлении к текущему

Слайд 32 Технология.
Шаг 1. Разбиение всего периода

Технология.Шаг 1. Разбиение всего периода действия контракта на интервалы.Шаг 2.

действия контракта на интервалы.
Шаг 2. Последовательный прогноз

изменения стоимости базисного актива по двум сценариям: снижение и увеличение.
Шаг 3. Определение премии в день исполнения для всех исходов.
Шаг 4. Расчет и корректировка премии в обратном направлении к текущему дню.

Слайд 33

Слайд 34 Обозначения и формулы (для опционов на акции)
u –

Обозначения и формулы (для опционов на акции)u – процент прироста стоимости

процент прироста стоимости базисного актива; d – процент падения;

p – вероятность роста базисного актива.




S – стоимость базисного актива



Слайд 35 Обозначения и формулы
П – премия опциона


Проверка

Обозначения и формулыП – премия опциона Проверка на исключение арбитража: Расчетная

на исключение арбитража:
Расчетная премия > прибыль при

исполнении
 расчетная премия
Расчетная премия < прибыль при исполнении
 прибыль от исполнения

Слайд 36 Поправки
Для опционов на фьючерсы




Для опционов на валюту


ПоправкиДля опционов на фьючерсыДля опционов на валюту

Слайд 37 Пример для бездивидендной акции

Пример для бездивидендной акции

Слайд 38 Условия
Покупка трехмесячного опциона пут на акции
Курс акции в

УсловияПокупка трехмесячного опциона пут на акцииКурс акции в момент заключения S=40Цена

момент заключения S=40
Цена исполнения Ци=45
Непрерывно начисляемая ставка без риска

r=10%
Стандартное отклонение акции σ=35%

Слайд 39 Решение
Δt=1/12=0.8(3)






1-p=0.4837

РешениеΔt=1/12=0.8(3) 1-p=0.4837

Слайд 40 Прогноз курса акции
Su=S*u=40*1.1063=44.25 Sd=S*d=40*0.9039=36.16
Расчет

Прогноз курса акции Su=S*u=40*1.1063=44.25 Sd=S*d=40*0.9039=36.16Расчет премии Su2: П=(0.5163*0+0.4387*0.75)*e-0.1*0.8333=0.36

премии
Su2: П=(0.5163*0+0.4387*0.75)*e-0.1*0.8333=0.36
Su :

П=(0.5163*0.36+0.4387*5)*e-0.1*0.8333=2.58
S : П=(0.5163*0.75+0.4387*8.84)*e-0.1*0.8333=4.6345-40=5

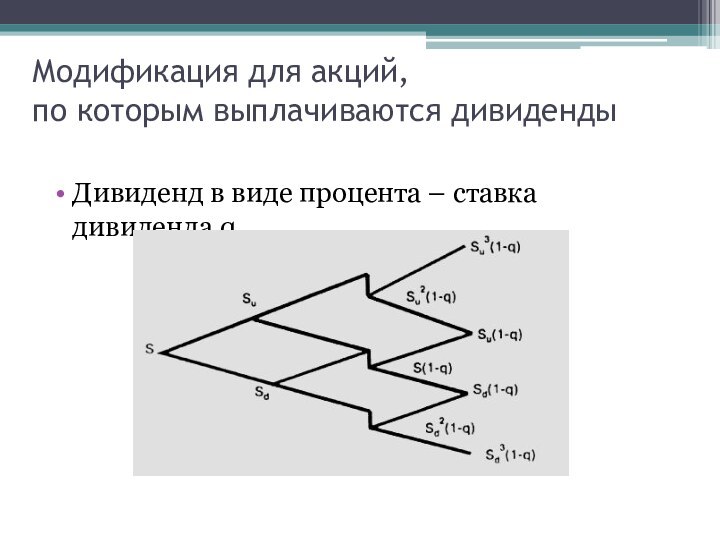
Слайд 41 Модификация для акций, по которым выплачиваются дивиденды
Дивиденд в

Модификация для акций, по которым выплачиваются дивидендыДивиденд в виде процента – ставка дивиденда q

виде процента – ставка дивиденда q

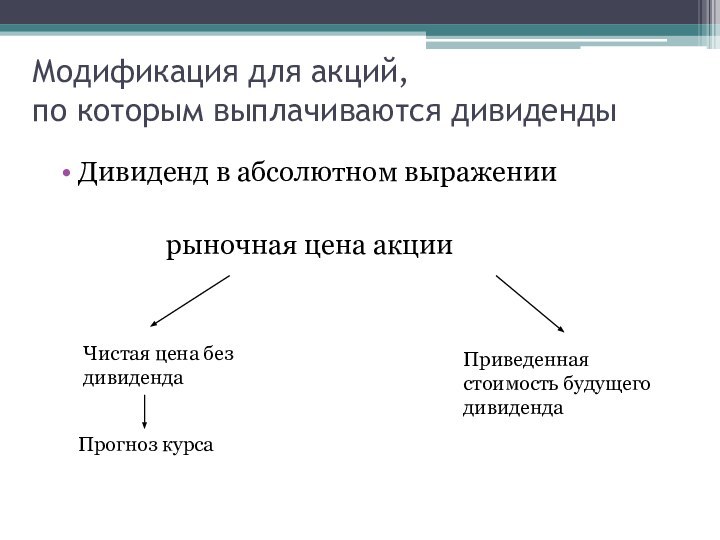
Слайд 42 Модификация для акций, по которым выплачиваются дивиденды
Дивиденд в

Модификация для акций, по которым выплачиваются дивидендыДивиденд в абсолютном выражении

абсолютном выражении

рыночная цена акции

Чистая цена без дивиденда

Приведенная стоимость будущего дивиденда

Прогноз курса

Слайд 43 Пример для опциона на акции, по которым выплачивается

Пример для опциона на акции, по которым выплачивается дивиденд в абсолютном выражении

дивиденд в абсолютном выражении

Слайд 44 Условия
Покупка опциона пут на четыре месяца
Текущий курс акции

УсловияПокупка опциона пут на четыре месяцаТекущий курс акции 48Цена исполнения Ци=45Стандартное

48
Цена исполнения Ци=45
Стандартное отклонение акции σ=35%
Непрерывно начисляемая ставка без

риска r=10%
Через 3 месяца дивиденд Д=3

Слайд 45 Решение
Приведенная стоимость дивиденда к текущему моменту
3*e-0.1*0.25=2.93

РешениеПриведенная стоимость дивиденда к текущему моменту 3*e-0.1*0.25=2.93 (0.25 – 3/12 года)Чистая

(0.25 – 3/12 года)
Чистая цена на текущий момент

48-2.93=45.07
p,u,d – см. пред. пример

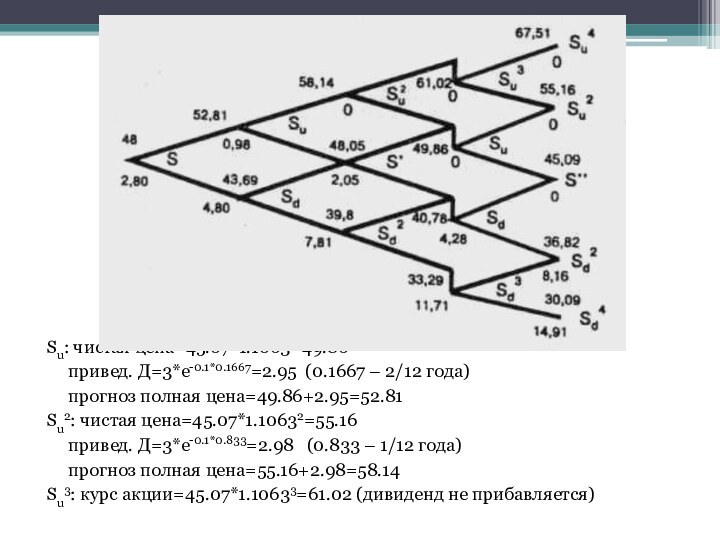
Слайд 46 Su: чистая цена=45.07*1.1063=49.86
привед. Д=3*e-0.1*0.1667=2.95 (0.1667

Su: чистая цена=45.07*1.1063=49.86 привед. Д=3*e-0.1*0.1667=2.95 (0.1667 – 2/12 года)

– 2/12 года)
прогноз полная цена=49.86+2.95=52.81
Su2: чистая

цена=45.07*1.10632=55.16
привед. Д=3*e-0.1*0.833=2.98 (0.833 – 1/12 года)
прогноз полная цена=55.16+2.98=58.14
Su3: курс акции=45.07*1.10633=61.02 (дивиденд не прибавляется)

Слайд 47 Простая биномиальная модель оценки премии опционов

Простая биномиальная модель оценки премии опционов

Слайд 48 Простая биномиальная модель оценки премии опциона
значение опциона и

Простая биномиальная модель оценки премии опциона значение опциона и курса акций рассматривается

курса акций рассматривается только в начале и конце некоторого

периода времени Т

Слайд 49 Простая биномиальная модель оценки премии европейского опциона call
Т0:

Простая биномиальная модель оценки премии европейского опциона callТ0: t – количество


t – количество месяцев;
Passet(T0) – цена актива в

момент Т0;
Pstrike – цена исполнения опциона;
i – ставка без риска;
P1asset(T1);
P2asset(T1)
? π Премия опциона

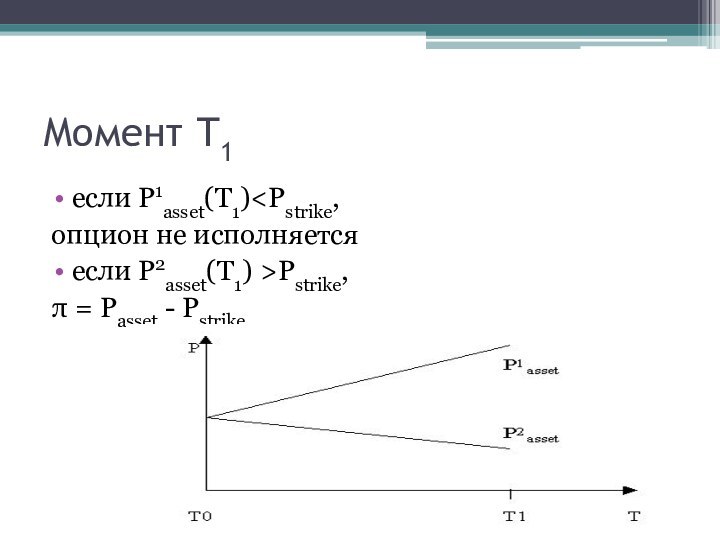
Слайд 50 Момент Т1
если P1asset(T1)Pstrikе,

Момент Т1если P1asset(T1)Pstrikе, π = Passet - Pstrike


π = Passet - Pstrike

Слайд 51 Портфель без риска
Портфель: покупка n акций и продажа

Портфель без рискаПортфель: покупка n акций и продажа 1опционаПортфель без риска,

1опциона
Портфель без риска, Vportfolio:
n*P1asset(T1) = n*P2asset(T1) – π

n =

π/[P1asset(T1) - P2asset(T1)]

Слайд 52 Стоимость портфеля
Т0:
Passet(T0)*n – π= Vportfolio*e-i*t/12

π = Passet(T0)*n –

Стоимость портфеляТ0:Passet(T0)*n – π= Vportfolio*e-i*t/12π = Passet(T0)*n – Vportfolio*e-i*t/12

Vportfolio*e-i*t/12

Слайд 53 Числовой пример
европейский опцион call
t=5 мес
Passet(T0)=$33;
Pstrike=$36;
i=10%;
P1asset(T1) =

Числовой примеревропейский опцион callt=5 месPasset(T0)=$33;Pstrike=$36; i=10%; P1asset(T1) = 34; P2asset(T1) =

34;
P2asset(T1) = 38
? π
$34*n = $38*n – 2

>>n = 0.5
$33*0.5- π = $16.5 – π
$16.5 – π = $17*e-0.1*5/12 =
= $16.31
 π =$0.19

Слайд 54 Недостатки модели
Не введен элемент вероятностной оценки
Ограничивается только двумя

Недостатки моделиНе введен элемент вероятностной оценкиОграничивается только двумя конечными значениями актива

конечными значениями актива

Слайд 55 Уравнение однопериодной биноминальной модели ценообразования европейских опционов put

Уравнение однопериодной биноминальной модели ценообразования европейских опционов put на акции ,

на акции , не выплачивающих дивиденды имеет вид :

Слайд 56 При построении

При построении «дерева решений» с большим количеством дат

«дерева решений» с большим количеством дат принятия решений применяются

те же принципы расчета стоимости реального опциона, что и для одноступенчатой модели. Однако чем больше узлов принятия решений, тем сложнее сделать оценку. На практике основные трудности использования биномиальной модели связаны с определением значений относительного роста и снижения стоимости бизнеса в каждом периоде, а также вероятностей положительного и негативного варианта развития событий. Для расчета этих параметров разработаны соответствующие формулы. Возможный рост стоимости бизнеса рассчитывается как: u = es, где u — относительный рост (значение данного параметра, например 1,25, означает ожидаемый рост стоимости проекта в 25%); s — стандартное отклонение среднегодовой стоимости проекта; h — интервал как часть года (к примеру, h = 0,5, если решение по проекту принимается раз в полгода). Относительное снижение стоимости (d) рассчитывается по формуле d= 1 : u.

Слайд 57 Модель Блэка - Шоулза

Модель Блэка - Шоулза

Слайд 58 Модель Блэка - Шоулза
Формула модели оценки опционов впервые

Модель Блэка - ШоулзаФормула модели оценки опционов впервые была выведена Фишером

была выведена Фишером Блэком и Майроном Шоулзом в 1973

году в статье «Оценка опционов и коммерческих облигаций» (The Pricing of Options and Corporate Liabilities)
Модель является частным случаем биномиальной модели.
Модель определяет равновесную цену колл, которая не позволяет получать арбитражный доход. Если в какой-то момент действительная цена опциона отличается от оценки по модели, то инвестор имеет возможность сформировать портфель путем продажи колл-опционов и покупки акций и без риска получить доходность, превышающую процентную ставку. Рост таких сделок приведет к выравниванию модельной оценки и действительной цены.

Цена опциона = =Текущая цена актива * N(d1) -
– Текущая оценка цены исполнения * N(d2)

Слайд 59 Модель Блэка-Шоулза
http://www.optionline.ru/optionCalculator/

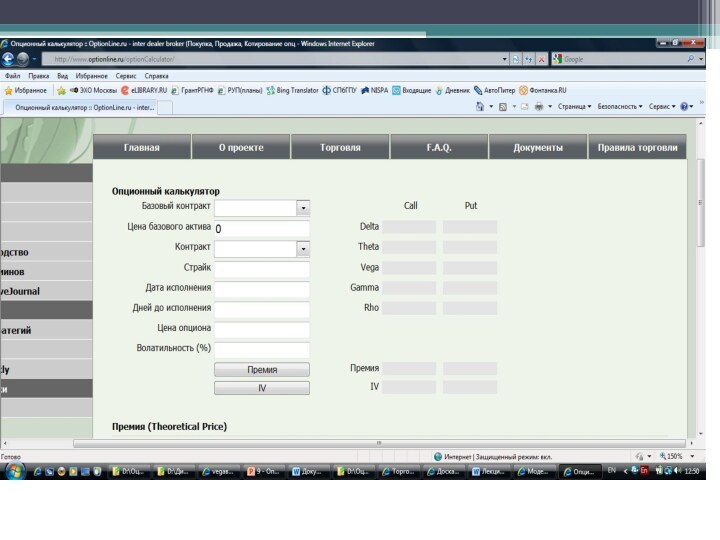
Модель Блэка-Шоулзаhttp://www.optionline.ru/optionCalculator/

Слайд 60 Модель Блэка-Шоулза (обозначения)
C(S,t) - текущая стоимость опциона call

Модель Блэка-Шоулза (обозначения)C(S,t) - текущая стоимость опциона call в момент t

в момент t до истечения срока опциона;
S - текущая

цена базисной акции;
N(x) - вероятность того, что отклонение будет меньше в условиях стандартного нормального распределения (таким образом, и ограничивают область значений для функции стандартного нормального распределения)
K - цена исполнения опциона;
r - безрисковая процентная ставка;
T − t - время до истечения срока опциона (период опциона);
σ - волатильность (квадратный корень из дисперсии) базисной акции.
 
(Для определения N(x) можно использовать таблицы для стандартной нормальной кривой или Excel-функцию HOPMCTPACП(x). Она возвращает стандартное нормальное интегральное распределение, которое имеет среднее, равное нулю, и стандартное отклонение, равное единице);

Слайд 61 Модель Блэка-Шоулза (для проектов)
где NPV1 – чистая дисконтированная

Модель Блэка-Шоулза (для проектов)где NPV1 – чистая дисконтированная стоимость проекта 1;

стоимость проекта 1;
Сор – стоимость опциона на инвестирование

во второй проект;
kс – коэффициент стоимости опциона;
PV2 - приведенные ДП 2 проекта (на момент начала осуществления первого проекта);
σ – стандартное отклонение цен на акции предприятия (уровень риска, связанный с данным предприятием);
Т – период времени, через который становится возможной реализация второго проекта;
– приведенная цена исполнения опциона (инвестиции в проект 2).

http://www.optionline.ru/optionCalculator/

Слайд 62 Факторы, определяющие стоимость опциона
Внутренняя стоимость
Текущая цена актива на

Факторы, определяющие стоимость опционаВнутренняя стоимостьТекущая цена актива на физическом рынке, цена

физическом рынке, цена спот
Цена исполнения опциона, цена страйк
Временная стоимость
Срок

действия опциона, т.е. время, остающееся до истечения срока действия опциона
Безрисковая процентная ставка
Волатильность цены базового актива

Слайд 63 Влияние факторов на премию опциона

Влияние факторов на премию опциона

Слайд 64

Слайд 65 При построении модели Блэк и Шоулз

При построении модели Блэк и Шоулз исходили из следующих условий:

исходили из следующих условий: 1)краткосрочные процентные ставки известны и не

меняются в течение времени; 2) цена акций меняется в течение времени случайным образом с дисперсией, пропорциональной квадрату из цены акции. Дисперсия доходов по акция является постоянной; 3)не учитываются операционные расходы на покупку/продажу опциона и акций, а также налоги; 4)краткосрочные кредитные и депозитные процентные ставки в течение срока действия опционного контракта одинаковы; 5)тип опциона – европейский Из этих условий вытекает, что цена опциона зависит только от цены акции и времени!

Слайд 66 Волатильность (Implied Volatility)
Волатильность бывает двух видов: подразумеваемая

Волатильность (Implied Volatility) Волатильность бывает двух видов: подразумеваемая (ожидаемая) волатильность (IV

(ожидаемая) волатильность (IV – Implied Volatility) и историческая волатильность

(HV – historical volatility).

Ожидаемая волатильность - основной рыночный параметр, определяющий стоимость опциона. Ожидаемая волатильность показывает ожидаемую рынком степень неопределенности цены базового актива в будущем. Чем больше значение ожидаемой волатильности, тем большую премию покупатель опциона готов заплатить продавцу.
Премия – стоимость опциона, вычисляемая на основе параметров модели Блэка-Шоулза.

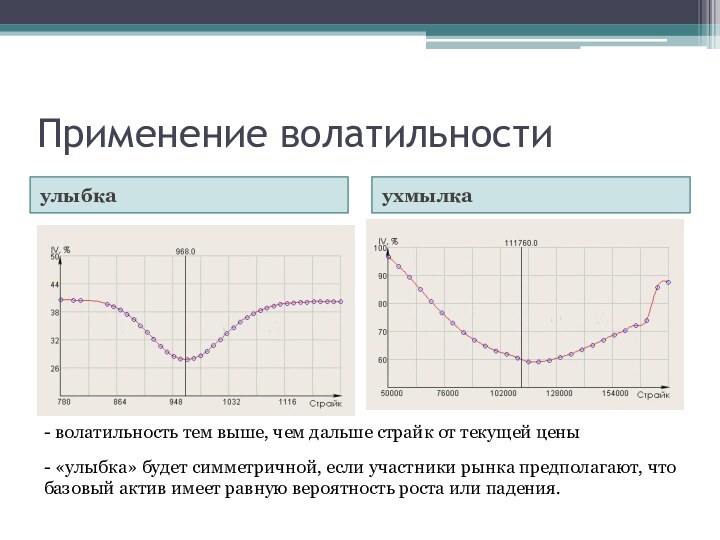
Слайд 67 Применение волатильности
улыбка
ухмылка
- волатильность тем выше, чем дальше страйк

Применение волатильностиулыбкаухмылка- волатильность тем выше, чем дальше страйк от текущей цены-

от текущей цены
- «улыбка» будет симметричной, если участники рынка

предполагают, что базовый актив имеет равную вероятность роста или падения.

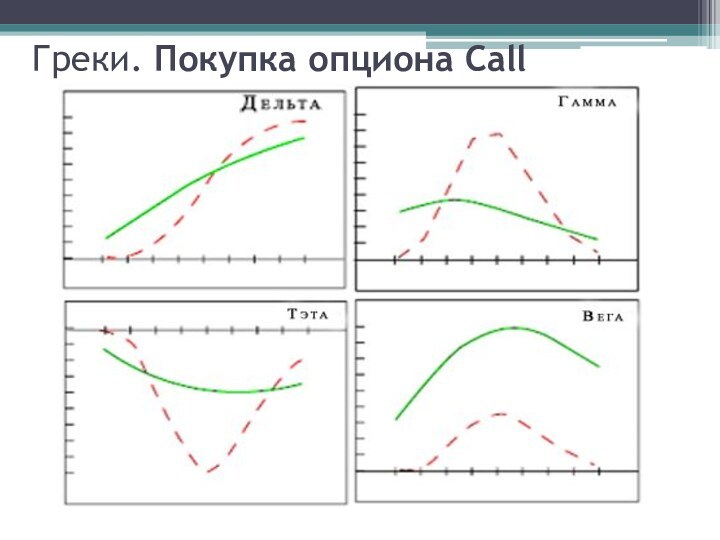
Слайд 68 Греки – это опционные характеристики, описывающие чувствительность цены

Греки – это опционные характеристики, описывающие чувствительность цены опциона к переменным

опциона к переменным модели
Delta
Дельта представляет собой первую частную

производную формулы Блэка-Шоулса по параметру цены базового актива. Дельта показывает скорость изменения цены опциона относительно изменения цены базового актива, лежащего в основе контракта. Графически, дельта - это угол наклона касательной к экспозиции прибылей и убытков. Дельта показывает на сколько изменится цена опциона при изменении цены базового актива на один пункт.
Gamma
Гамма представляет собой вторую частную производную формулы Блэка-Шоулса по параметру цены базового актива. Гамма показывает скорость изменения дельты по отношению к изменению цены базового актива, лежащего в основе опциона. Графически, гамма - это угол наклона касательной к экспозиции дельты или кривизна экспозиции прибылей и убытков. Поэтому гамму называют еще кривизной опциона. Гамма измеряется в «дельтах» на один пункт изменения цены базового актива.


Слайд 69 Греки
Тета представляет собой первую частную производную формулы Блэка-Шоулса

ГрекиТета представляет собой первую частную производную формулы Блэка-Шоулса по параметру времени

по параметру времени до экспирации. Тета показывает с какой

скоростью падает цена опциона по мере приближения срока истечения контракта при сохранении прочих параметров опциона неизменными. Стоимость опциона будет постепенно приближаться по величине к внутренней стоимости опциона по мере приближения срока истечения контракта. Практически для всех опционов значения теты и гаммы будут иметь противоположные знаки. Взаимосвязь между этими греками также проявляется в величине их значения, а именно: высокой положительной тете будет соответствовать большая отрицательная гамма, и наоборот. Большая тета говорит о том, что существует высокий риск обесценивания опциона по мере приближения срока экспирации контракта.
Vega
Вега представляет собой первую частную производную формулы Блэка-Шоулса по параметру ожидаемой волатильности. Вега представляет собой отношение изменения величины премии опциона к изменению ожидаемой волатильности. Этот грек показывает на сколько пунктов изменится цена опциона при изменении ожидаемой волатильности на один процентный пункт.
Rho
Ро представляет собой первую частную производную формулы Блэка-Шоулса по параметру безрисковой ставки. Ро показывает на сколько измененится цена опциона при изменении процентной ставки на один процент. Премия колл-опциона положительно зависит от процентной ставки, пут-опциона - отрицательно. На практике Ро важно учитывать для долгосрочных опционов, так как для коротких периодов времени влияние процентной ставки на премию опциона незначительно. Ро измеряется в денежных единицах.

http://lowrisk.ru/category/option_simple/

Слайд 70

Слайд 71 Греки. Покупка опциона Call

Греки. Покупка опциона Call

Слайд 72 Интересные особенности ценообразования для европейского опциона «колл».
Можно показать,

Интересные особенности ценообразования для европейского опциона «колл».Можно показать, что произойдет с

что произойдет с действительной ценой опциона «колл» при изменении

одной из переменных, когда остальные четыре сохраняют свои значения.
1. Чем выше цена базисной акции , тем больше стоимость опциона «колл».
2. Чем выше цена исполнения, тем меньше стоимость опциона «колл».
3. Чем больше времени до даты истечения, тем больше стоимость опциона «колл».
4. Чем выше ставка без риска, тем больше стоимость опциона «колл».
5. Чем больше риск обыкновенной акции, тем больше стоимость опциона «колл».

Слайд 73 Выигрыши и потери при различных стратегиях

Выигрыши и потери при различных стратегиях

Слайд 74 Оценка портфеля опционов
Оценка портфеля опционов

Оценка портфеля опционов Оценка портфеля опционов

Слайд 75 5. Опционный подход

5. Опционный подход

Слайд 76 Реальные опционы и инвестиции фирмы
Реальный опцион – право менеджмента

Реальные опционы и инвестиции фирмыРеальный опцион – право менеджмента принять решениеПраво

принять решение
Право менеджера может иметь стоимость в условиях неопределенности
Право

менеджера реализуется с разрешением неопределенности
Неопределенность может увеличивать стоимость инвестиционных проектов
Стоимость проекта базируется на NPV и включает стоимость управленческой гибкости:

Стоимость = NPV + стоимость реального опциона

Слайд 77 Входные параметры

Входные параметры

Слайд 78 Правила принятия решений

Правила принятия решений

Слайд 79 Методология оценки
Формирование портфеля-копии (дублирующего будущие денежные потоки) с

Методология оценкиФормирование портфеля-копии (дублирующего будущие денежные потоки) с использованием:Базового актива (акции

использованием:
Базового актива (акции для финансового опциона и NPV для

инвестиционного проекта)
Безрисковых бескупонных облигаций
Стоимость портфеля-копии в настоящий момент при отсутствии арбитражных возможностей должна быть равна стоимости финансового или реального опциона

Слайд 80 Методология оценки

Методология оценки

Слайд 81 Методология оценки

Методология оценки

Слайд 82 Методология оценки

Методология оценки

Слайд 83 Методология оценки

Методология оценки

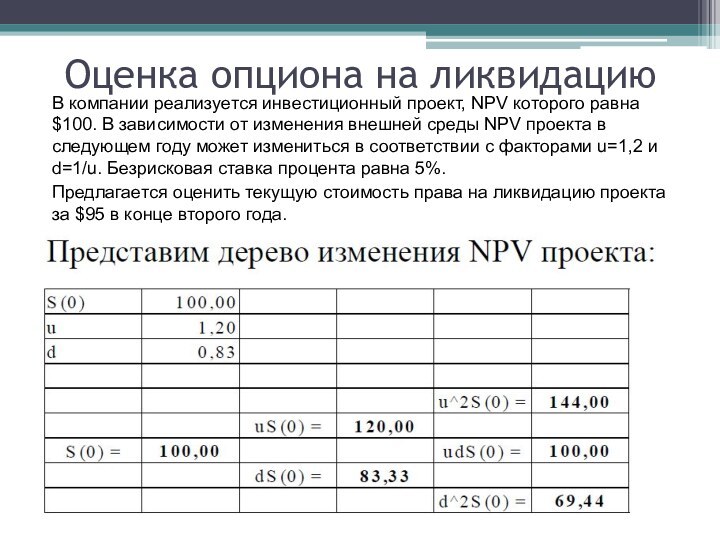
Слайд 84 Оценка опциона на ликвидацию
В компании реализуется инвестиционный проект,

Оценка опциона на ликвидациюВ компании реализуется инвестиционный проект, NPV которого равна

NPV которого равна $100. В зависимости от изменения внешней

среды NPV проекта в следующем году может измениться в соответствии с факторами u=1,2 и d=1/u. Безрисковая ставка процента равна 5%.
Предлагается оценить текущую стоимость права на ликвидацию проекта за $95 в конце второго года.

Слайд 85 Оценка опциона на ликвидацию
Изначально, стоимость опциона на ликвидацию

Оценка опциона на ликвидациюИзначально, стоимость опциона на ликвидацию можновычислить только на

можно
вычислить только на момент окончания второго периода:
Определим стоимость опциона

в момент истечения
первого периода в случае уменьшения NPV проекта.

Слайд 86 Оценка опциона на ликвидацию
Таким образом, в конце первого

Оценка опциона на ликвидациюТаким образом, в конце первого периода в случае

периода в случае уменьшении NPV
проекта, право на ликвидацию проекта

за $95 через 1 период
составит $9,96. Аналогичным образом необходимо определить
сначала стоимость опциона в первом периоде в случае увеличения
NPV проекта, а в дальнейшем стоимость права ликвидации в
настоящий момент.

Слайд 87 Оценка опциона на ликвидацию

Оценка опциона на ликвидацию

Слайд 88 Рискнейтральный подход к оценке

Рискнейтральный подход к оценке

Слайд 89 Рискнейтральный подход к оценке

Рискнейтральный подход к оценке

Слайд 90 Особенности оценки портфеля реальных опционов

Особенности оценки портфеля реальных опционов

Слайд 91 Особенности метода реальных опционов

Особенности метода реальных опционов

Слайд 92 Преимущества и недостатки метода реальных опционов
Преимущества

дает

Преимущества и недостатки метода реальных опционов Преимущества дает более объективную и

более объективную и многостороннюю оценку

позволяет предусмотреть большое количество

вариантов для каждого этапа его реализации
позволяет учесть большее количество факторов

Недостатки

Некритичное применение этой методологии может негативно влиять на бизнес компании и ее конкурентную позицию.

Отсутствие квалифицированных специалистов

внедрение модели реальных опционов требует изменения подходов к ведению бизнеса


Слайд 93 С точки зрения оценки бизнеса нас интересуют следующие

С точки зрения оценки бизнеса нас интересуют следующие типы опционов:

типы опционов:

Слайд 94 Примеры

Примеры

Слайд 95

Расчет K=30000 S=18000 r=4,3%

Расчет K=30000 S=18000 r=4,3% T=3 Для начала

нужно рассчитать значение функции нормального распределения: N(d1)=0,3962 N(d2)=0,1842 И по формуле Блека-Сколеса стоимость опциона будет составлять 2 332,86 д.е.

Слайд 96 Пример 2. Опцион на отказ.
Технология А предусматривает использование

Пример 2. Опцион на отказ.Технология А предусматривает использование заказного оборудования, управляемого

заказного оборудования, управляемого с помощью компьютера, для производства деталей

сложной формы, которые необходимы для нового типа двигателя в большом количестве и с низкими издержками. Но если новый двигатель не найдет своего покупателя, то данное оборудование окажется совершенно бесполезным.
Технология Б предусматривает использование стандартных станков. Затраты на оплату труда будут намного выше, но данное оборудование можно продать или модернизировать в случае, если новый тип двигателя не будет продаваться.

Слайд 97 Пример 3.Опцион на выбор времени.
Текущая стоимость = $

Пример 3.Опцион на выбор времени.Текущая стоимость = $ 200 млн. В

200 млн. В случае высокого спроса в будущем стоимость

проекта возрастает до $ 250 млн, а в случае низкого спроса падает до $ 160 млн.
Если вы отложите инвестиции, то потеряете денежный поток первого года ($ 160 млн или $ 250 млн), но зато сможете избежать большой ошибки — инвестиций в размере $ 200 млн в проект, стоимость которого в будущем может составить всего $ 160 млн.

Слайд 98 Пример 4
Предположим, что компания рассматривает проект стоимостью $

Пример 4Предположим, что компания рассматривает проект стоимостью $ 4 млн и

4 млн и его конечный результат зависит от спроса

на продукт в течение первого года. В настоящее время предсказать спрос чрезвычайно сложно, поскольку он напрямую зависит от возможности производства конкурирующего товара, что, в свою очередь, зависит от успешности новой, никем прежде не испытанной технологии. Однако вся эта неопределенность будет полностью устранена к концу первого года.
Если спрос в течение первого года будет высоким, на уровне $ 600 тыс. в реальном выражении, то спрос со второго года до бесконечности ожидается тоже на уровне $ 600 тыс. (опять в реальном выражении и весьма упрощенно). Мы также предполагаем, что соответствующая реальная ставка дисконтирования равна 10%, так что стоимость этого денежного потока за бесконечный период составит $ 6 млн. Если же, напротив, к концу первого года спрос окажется низким ($ 300 тыс.), то так будет вечно, а текущая стоимость проекта составит $ 3 млн.

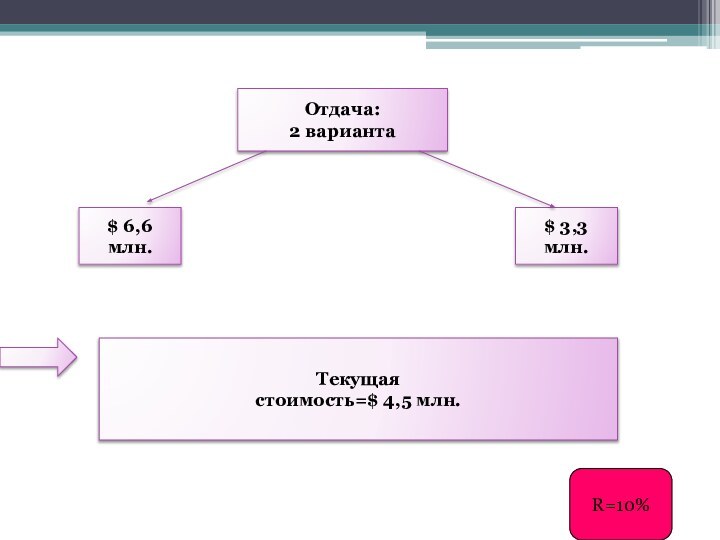
Слайд 99 Отдача:
2 варианта
$ 6,6 млн.
Текущая
стоимость=$ 4,5 млн.
$

Отдача: 2 варианта$ 6,6 млн.Текущая стоимость=$ 4,5 млн.$ 3,3 млн.R=10%

3,3 млн.
R=10%

Слайд 100 DCF
$ 4,5 млн. - $ 4 млн. =

DCF$ 4,5 млн. - $ 4 млн. = $ 500 тыс.Проект можно запускать

$ 500 тыс.
Проект можно запускать

Слайд 101 Решение с помощью метода реальных опционов
Используем биномиальную модель

Решение с помощью метода реальных опционовИспользуем биномиальную модель опционного ценообразования.Допустим, безрисковая

опционного ценообразования.

Допустим, безрисковая ставка находится на уровне 5%. Мы

сможем застраховать свой портфель от возможного падения цен в том случае, если запишем 1 / 0,6061 = 1,65 опциона на покупку по проекту. Поскольку гарантированная отдача будет не меньше чем $ 3,3 млн, то стоимость опциона на покупку, С, можно найти из следующего уравнения:

( 4,5 млн. – 1,65С)*1,05=3,3 млн.

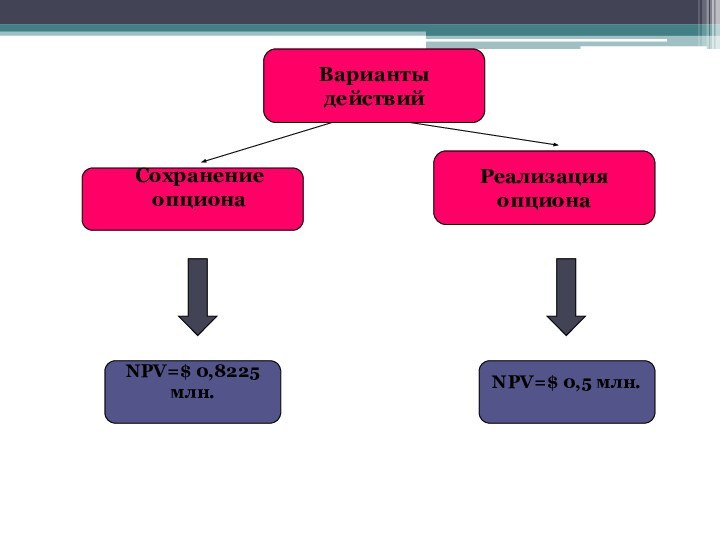
Слайд 102 Варианты действий
Сохранение опциона

Реализация опциона
NPV=$ 0,8225 млн.

NPV=$ 0,5 млн.

Варианты действийСохранение опционаРеализация опционаNPV=$ 0,8225 млн.NPV=$ 0,5 млн.

Слайд 103 Бизнес-решения, принятые на основе теории реальных опционов
слияние Time

Бизнес-решения, принятые на основе теории реальных опционовслияние Time Warner и AOL

Warner и AOL с целью расширения дистрибутивной сети за

счет онлайновой среды;
решение портала Yahoo! об освоении бизнеса интернет-аукционов;
покупка eBay таких компаний, как Half.com и Butterfield & Butterfield.

Слайд 104 Появление метода реальных опционов — это важный шаг

Появление метода реальных опционов — это важный шаг в развитии анализа

в развитии анализа эффективности. Возможность количественного учета управленческой гибкости

позволяет менеджменту принимать качественно новые решения в условиях высокой неопределенности.

Слайд 105 ОПЦИОНЫ: описание, графики, калькуляция
http://www.optiondesk.ru/?code=information
http://optiontraders.ru/2008/04/29/vertikalnye-spredy/

ОПЦИОНЫ: описание, графики, калькуляцияhttp://www.optiondesk.ru/?code=informationhttp://optiontraders.ru/2008/04/29/vertikalnye-spredy/

Слайд 106 Калькуляция стоимости сложных опционов
На практике чаще всего встречаются

Калькуляция стоимости сложных опционовНа практике чаще всего встречаются весьма сложные реальные

весьма сложные реальные опционы. Они бывают двух типов: опционы

на покупку (колл-опционы) и опционы на продажу (пут-опционы).

Опцион на покупку подразумевает право, но не обязательство, приобрести актив по фиксированной цене (цене исполнения) на определенную дату (европейский опцион на покупку) или до истечения определенной даты (американский опцион на покупку).

Опцион на продажу представляет собой право, но не обязательство, продать актив по фиксированной цене в будущем; они также бывают американскими и европейскими.

Слайд 107 Паритет опционов на покупку и продажу
Существует хорошо известная

Паритет опционов на покупку и продажуСуществует хорошо известная зависимость между стоимостью

зависимость между стоимостью колл и пут-опционов, которая основана на

том факте, что выигрыш в момент истечения срока владения опционом на покупку акций аналогичен вместе взятым выигрышу от владения акцией и опциону на продажу по цене исполнения, равной цене опциона на покупку. И то, и другое позволяет инвестору застраховаться от падения курса акций и выиграть на разнице между курсом акций и ценой исполнения в случае, если цена акций возрастет. Разница лишь в том, что стратегия, основанная на владении только опционами, требует меньше инвестиций, поскольку цену исполнения не придется выплачивать до истечения срока действия опциона.

Таким образом, разница между двумя альтернативами равна текущему значению цены исполнения.

Слайд 108 Стоимость опциона на покупку + текущее значение цены

Стоимость опциона на покупку + текущее значение цены исполнения = стоимость

исполнения = стоимость опциона на продажу + цена акции


Стоимость

опциона на продажу = стоимость опциона на покупку – цена акции + текущее значение цены исполнения.

Слайд 109

Слайд 110 Покупка опциона кол л. Long Call.
Прямое создание Лонг Колл

Покупка опциона кол л. Long Call. Прямое создание Лонг Колл А

А Описание Самая простая и наиболее популярная стратегия. Характеризуется неограниченой возможной

прибылью при благоприятном развитии событий на рынке и ограниченым убытком если базовый актив снижается или стоит на месте.
Синтетическое создание Лонг Пут А. Лонг базовый инструмент Используется, если Ожидается, что цена базового актива и его волатильность повысятся. Прибыль Неограничена. Убыток Ограничен премией уплаченной за опцион.

Ниже представлено графическое изображение покупки опциона Call.

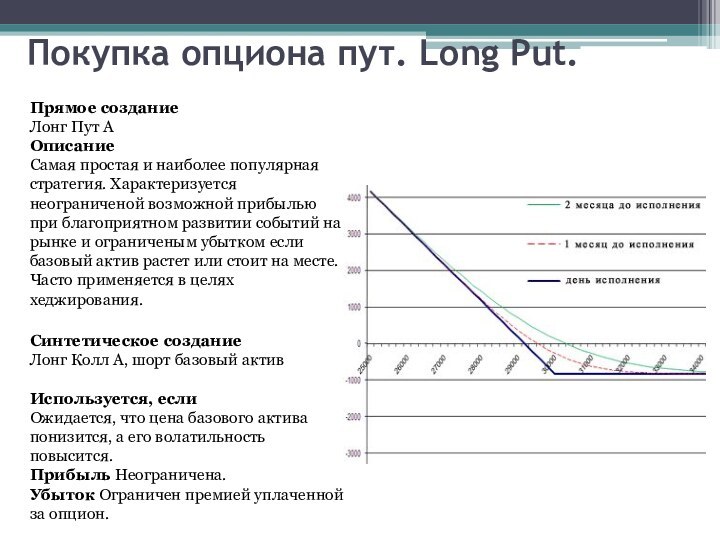
Слайд 111 Покупка опциона пут. Long Put.
Прямое создание Лонг Пут А Описание Самая

Покупка опциона пут. Long Put. Прямое создание Лонг Пут А Описание

простая и наиболее популярная стратегия. Характеризуется неограниченой возможной прибылью

при благоприятном развитии событий на рынке и ограниченым убытком если базовый актив растет или стоит на месте. Часто применяется в целях хеджирования.
Синтетическое создание Лонг Колл А, шорт базовый актив Используется, если Ожидается, что цена базового актива понизится, а его волатильность повысится. Прибыль Неограничена. Убыток Ограничен премией уплаченной за опцион.

Слайд 112 Продажа опциона колл. Short Call.
Описание Одна из самых простых

Продажа опциона колл. Short Call. Описание Одна из самых простых стратегий.

стратегий. Однако ее применение требует большой осторожности, так как

в этом случае прибыль ограничена, а убыток ничем не ограничен. Часто применяется в сложных стратегиях с использованием страхующих составляющих, например, при продаже волатильности дополнительно открывается длинная позиция по базовому активу.
Синтетическое создание Шорт Пут А, шорт базовый инструмент Используется, если Ожидается, что цена базового актива и его волатильность понизятся. Прибыль Ограничена премией полученной за опцион. Убыток Неограничен.

Слайд 113 Продажа опциона пут. Short Put.
Описание Одна из самых простых

Продажа опциона пут. Short Put. Описание Одна из самых простых стратегий.

стратегий. Однако ее применение требует большой осторожности, так как

в этом случае прибыль ограничена, а убыток ничем не ограничен. Часто применяется в сложных стратегиях с использованием страхующих составляющих, например, при продаже волатильности дополнительно открывается короткая позиция по базовому активу.
Синтетическое создание Шорт Колл А. лонг базовый актив Используется, если Ожидается, что цена базового актива повысится, а его волатильность понизится. Прибыль Ограничена премией уплаченной за опцион Убыток Неограничен.

Слайд 114 Введение
Опцион – срочный контракт, дающий право, но не

ВведениеОпцион – срочный контракт, дающий право, но не обязанность купить/продать базовый

обязанность купить/продать базовый актив по определенной цене в определенный

момент времени в будущем, в обмен на уплаченную премию.
Страйк – цена исполнения опциона.
Опционы дают возможность:
Занимать позиции в любом направлении при заранее ограниченных убытках.
Максимизировать прибыль как при значительных, так и при незначительных движениях рынка.
Зарабатывать на боковом движении рынка и при неопределенных «взрывных» движениях в любую сторону.
Эффективно хеджировать позиции по базовому активу.

Слайд 115 Определения

Опцион call - дает право, но не обязанность

ОпределенияОпцион call - дает право, но не обязанность купить базовый актив

купить базовый актив по цене страйк в определенный срок
Опцион

put - дает право, но не обязанность продать базовый актив по цене страйк в определенный срок
ATM – опцион у денег (at-the-money), когда цена базового актива совпадает со страйком
OTM - опцион вне денег (оut-of-money), когда страйк опциона CALL выше цены базового актива или страйк опциона PUT ниже цены базового актива
ITM - опцион в деньгах (in-the-money), когда страйк опциона CALL ниже цены базового актива или страйк опциона PUT выше цены базового актива

Слайд 116 Направленные позиции
«Бычья» позиция:
Покупка опционов call
Продажа опционов

Направленные позиции«Бычья» позиция: Покупка опционов call Продажа опционов putПокупка call-спредаПродажа put-спреда

put
Покупка call-спреда
Продажа put-спреда

Слайд 117 Цена на момент исполнения
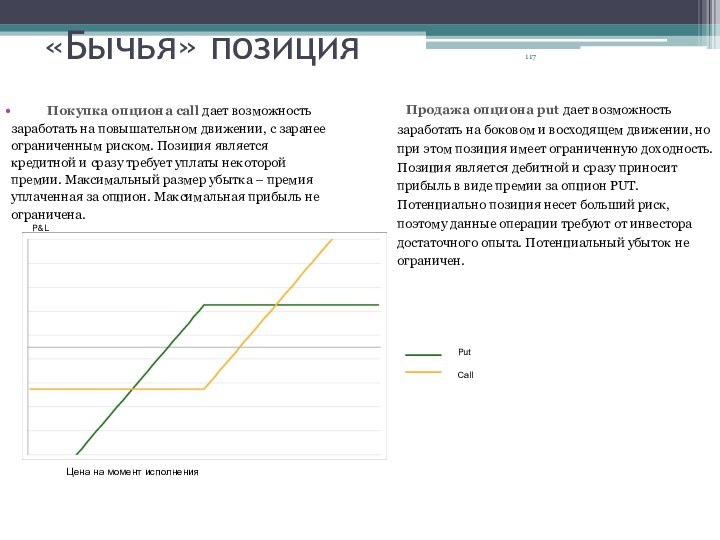
«Бычья» позиция
Покупка опциона call дает

Цена на момент исполнения«Бычья» позиция Покупка опциона call дает возможность заработать на

возможность заработать на повышательном движении, с заранее ограниченным риском.

Позиция является кредитной и сразу требует уплаты некоторой премии. Максимальный размер убытка – премия уплаченная за опцион. Максимальная прибыль не ограничена.

Продажа опциона put дает возможность заработать на боковом и восходящем движении, но при этом позиция имеет ограниченную доходность. Позиция является дебитной и сразу приносит прибыль в виде премии за опцион PUT. Потенциально позиция несет больший риск, поэтому данные операции требуют от инвестора достаточного опыта. Потенциальный убыток не ограничен.

P&L

Call

Put

Слайд 118 Цена на момент исполнения
Покупка call- спреда – покупка

Цена на момент исполнения Покупка call- спреда – покупка ATM или ITM

ATM или ITM опциона call и одновременная продажа OTM

опциона call. Таким образом позиция частично финансируется за счет премии дальнего опциона call. Позиция является кредитной.
. Продажа put-спреда – покупка OTM опциона put и продажа ATM или ITM опциона put. Позиция является дебитной и сразу приносит прибыль равную разнице премий за опционы put.
Обе позиции обладают ограниченным риском и ограниченной прибылью.

««Бычья» позиция Бычья» позиция

P&L

Покупка сall-спреда

Продажа рut-спреда


Слайд 119 Направленные позиции
«Медвежья» позиция:
Покупка опционов put
Продажа опционов call
Покупка

Направленные позиции«Медвежья» позиция:Покупка опционов putПродажа опционов call Покупка put-спредаПродажа call-спреда

put-спреда
Продажа call-спреда


Слайд 120 Цена на момент исполнения
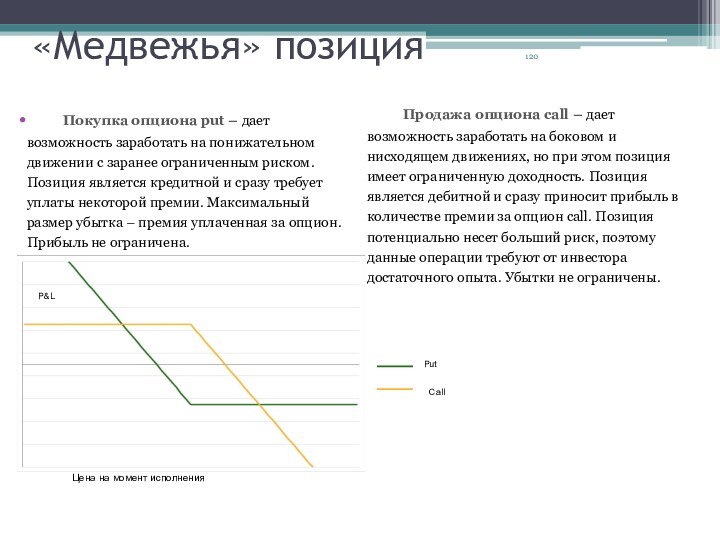
«Медвежья» позиция
Покупка опциона put –

Цена на момент исполнения«Медвежья» позиция Покупка опциона put – дает возможность заработать

дает возможность заработать на понижательном движении с заранее ограниченным

риском. Позиция является кредитной и сразу требует уплаты некоторой премии. Максимальный размер убытка – премия уплаченная за опцион. Прибыль не ограничена.

P&L

Call

Put

Продажа опциона call – дает возможность заработать на боковом и нисходящем движениях, но при этом позиция имеет ограниченную доходность. Позиция является дебитной и сразу приносит прибыль в количестве премии за опцион call. Позиция потенциально несет больший риск, поэтому данные операции требуют от инвестора достаточного опыта. Убытки не ограничены.

Слайд 121 Цена на момент исполнения
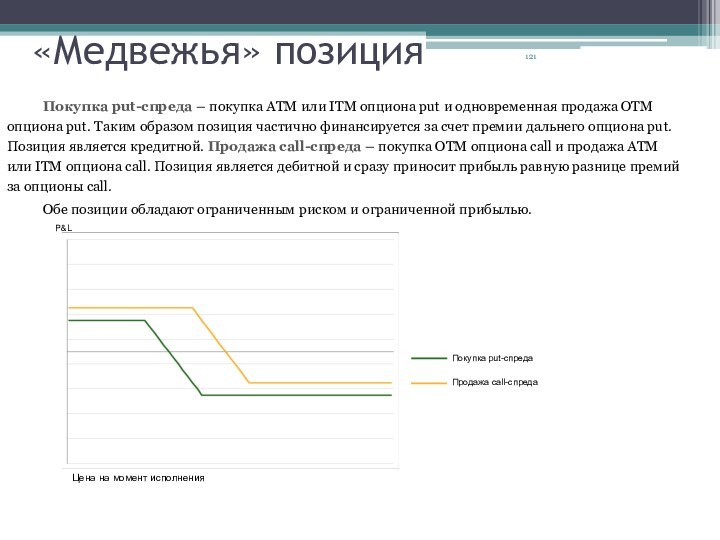
Покупка put-спреда – покупка ATM

Цена на момент исполнения Покупка put-спреда – покупка ATM или ITM опциона

или ITM опциона put и одновременная продажа OTM опциона

put. Таким образом позиция частично финансируется за счет премии дальнего опциона put. Позиция является кредитной. Продажа call-спрeда – покупка OTM опциона call и продажа ATM или ITM опциона call. Позиция является дебитной и сразу приносит прибыль равную разнице премий за опционы call.
Обе позиции обладают ограниченным риском и ограниченной прибылью.





«Медвежья» позиция


P&L

Продажа call-спреда

Покупка put-спреда

Слайд 122 Cтратегии покупки/продажи волатильности
Стредл (straddle)
Стренгл (strangle)

Cтратегии покупки/продажи волатильности Стредл (straddle) Стренгл (strangle)

Слайд 123 Цена на момент исполнения
Стредл – одновременная покупка опционов

Цена на момент исполнения Стредл – одновременная покупка опционов put и call

put и call с одним страйком и одним сроком

исполнения.
Стренгл – одновременная покупка опционов put и call с разными страйками и одним сроком исполнения.
Стратегии приносят прибыль при сильных, быстрых движениях рынка – росте/падении цены базового актива либо росте волатильности. Убыток позиции ограничен величиной уплаченной премии за опционы put и call. Стоимость покупки стренгла несколько ниже стредла и требует большего ценового движения для окупаемости.

Покупка Стредла и Стренгла

P&L

Стредл

Стренгл

Слайд 124 Цена на момент исполнения
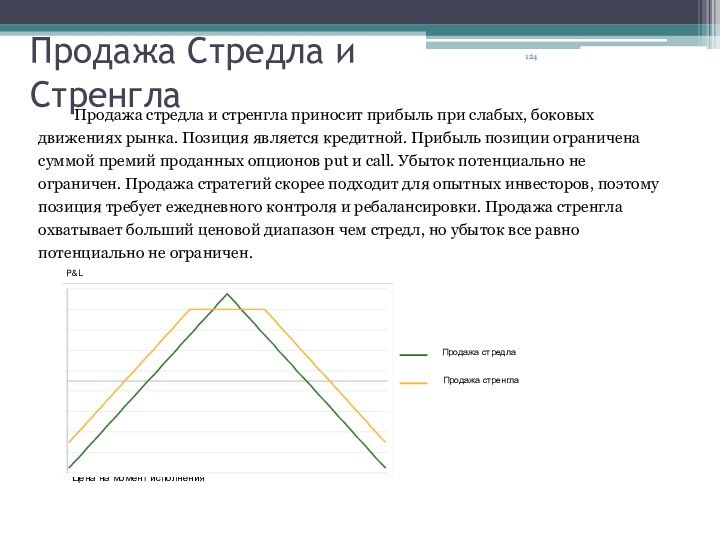
Продажа Стредла и Стренгла
P&L
Продажа стредла
Продажа

Цена на момент исполненияПродажа Стредла и СтренглаP&LПродажа стредлаПродажа стренгла Продажа стредла и

стренгла
Продажа стредла и стренгла приносит прибыль при слабых, боковых

движениях рынка. Позиция является кредитной. Прибыль позиции ограничена суммой премий проданных опционов put и call. Убыток потенциально не ограничен. Продажа стратегий скорее подходит для опытных инвесторов, поэтому позиция требует ежедневного контроля и ребалансировки. Продажа стренгла охватывает больший ценовой диапазон чем стредл, но убыток все равно потенциально не ограничен.

Слайд 125 Опционная стратегия с удержанием базового актива



Zero-premium collar
Put-spread collar
Покрытая

Опционная стратегия с удержанием базового активаZero-premium collarPut-spread collarПокрытая продажа опциона

продажа опциона

Слайд 126 Цена на момент исполнения
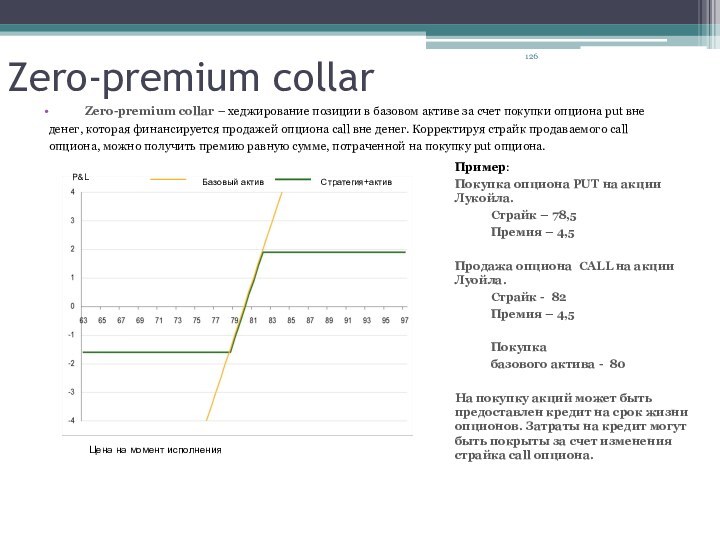
Zero-premium collar
Zero-premium collar – хеджирование

Цена на момент исполненияZero-premium collar Zero-premium collar – хеджирование позиции в базовом

позиции в базовом активе за счет покупки опциона put

вне денег, которая финансируется продажей опциона call вне денег. Корректируя страйк продаваемого call опциона, можно получить премию равную сумме, потраченной на покупку put опциона.

Стратегия+актив

Базовый актив

P&L

Пример:
Покупка опциона PUT на акции Лукойла.
Страйк – 78,5
Премия – 4,5

Продажа опциона CALL на акции Луойла.
Страйк - 82
Премия – 4,5

Покупка
базового актива - 80

На покупку акций может быть предоставлен кредит на срок жизни опционов. Затраты на кредит могут быть покрыты за счет изменения страйка call опциона.

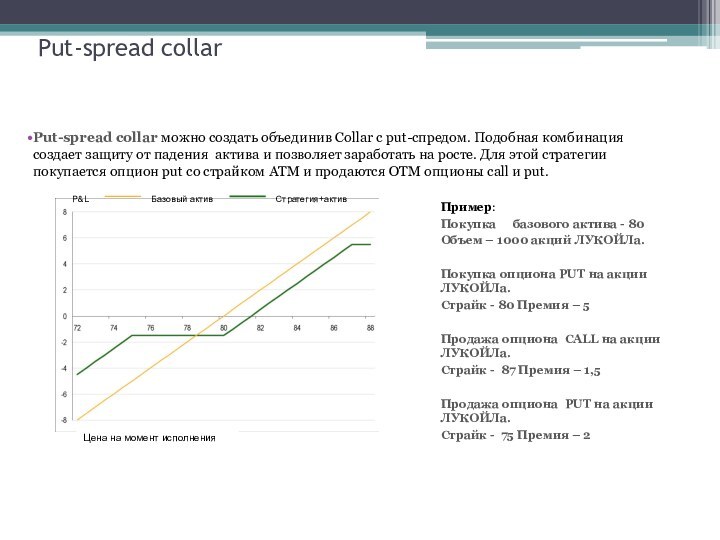
Слайд 127 Put-spread collar
Put-spread collar можно создать объединив Collar с

Put-spread collarPut-spread collar можно создать объединив Collar с put-спредом. Подобная комбинация

put-спредом. Подобная комбинация создает защиту от падения актива и

позволяет заработать на росте. Для этой стратегии покупается опцион put cо страйком ATM и продаются OTM опционы call и put.

Пример:
Покупка базового актива - 80
Объем – 1000 акций ЛУКОЙЛа.

Покупка опциона PUT на акции ЛУКОЙЛа.
Страйк - 80 Премия – 5

Продажа опциона CALL на акции ЛУКОЙЛа.
Страйк - 87 Премия – 1,5

Продажа опциона PUT на акции ЛУКОЙЛа.
Страйк - 75 Премия – 2






Стратегия+актив

Базовый актив

P&L

Цена на момент исполнения

  • Имя файла: optsionnye-modeli.pptx
  • Количество просмотров: 128
  • Количество скачиваний: 0
- Предыдущая Победа
Следующая - Нанотехнологии

Похожие презентации

Музыкальный остров Музыкальный остров 197
Презентация по французскому языку на тему Прогулки по Парижу (9 класс) Презентация по французскому языку на тему Прогулки по Парижу (9 класс) 113
Презентация по почтовой связи на тему Виды почтовой связи Презентация по почтовой связи на тему Виды почтовой связи 178
Социально-экономическое развитие Брянской области Социально-экономическое развитие Брянской области 133
Презентация Раз в крещенский вечерок... Внеклассная работа Презентация Раз в крещенский вечерок... Внеклассная работа 224
Презентация Азбука для родителей презентация к уроку по теме Презентация Азбука для родителей презентация к уроку по теме 103
Методические особенности организации мотивации и рефлексии на учебном занятии презентация к уроку Методические особенности организации мотивации и рефлексии на учебном занятии презентация к уроку 125
Статья Особенности игровой деятельности во время адаптации ребенка к детскому саду статья (младшая группа) Статья Особенности игровой деятельности во время адаптации ребенка к детскому саду статья (младшая группа) 112
История Чернобыля в памяти народа История Чернобыля в памяти народа 122
Использование игровых приемов к овладению нетрадиционными изобразительными технологиями в работе с бумагой. презентация к занятию по конструированию, ручному труду (средняя группа) по теме Использование игровых приемов к овладению нетрадиционными изобразительными технологиями в работе с бумагой. презентация к занятию по конструированию, ручному труду (средняя группа) по теме 110
blokada 4 blokada 4 111
elektronnoe portfolio - 1 chast elektronnoe portfolio - 1 chast 124
Презентация: Инновационные технологии социально-коммуникативного развития детей старшего дошкольного возраста презентация Презентация: Инновационные технологии социально-коммуникативного развития детей старшего дошкольного возраста презентация 79
Анимация Анимация 109
Презентация - Викторина по сказке А.С. Пушкина - Начальная школа Презентация - Викторина по сказке А.С. Пушкина - Начальная школа 151
Физико-математические аспекты нефтегазового дела Физико-математические аспекты нефтегазового дела 131
Презентация родительского собрания в средней группе на начало года презентация к уроку (средняя группа) Презентация родительского собрания в средней группе на начало года презентация к уроку (средняя группа) 53
СЕРЕБРЯНЫЙ ВЕК РУССКОЙ ЛИТЕРАТУРЫ СЕРЕБРЯНЫЙ ВЕК РУССКОЙ ЛИТЕРАТУРЫ 176
Воспитание дошкольников посредством реализации вариативной части ООП Братковского детского сада Край родной презентация к уроку (старшая группа) Воспитание дошкольников посредством реализации вариативной части ООП Братковского детского сада Край родной презентация к уроку (старшая группа) 117
Проект Шестиногие малыши вторая младшая группа проект (младшая группа)                          Проект Шестиногие малыши Проект Шестиногие малыши вторая младшая группа проект (младшая группа)                          Проект Шестиногие малыши 110
Презентация по украинскому языку на тему Стилистика(10 класс) Презентация по украинскому языку на тему Стилистика(10 класс) 121
Кружок для детей Вкусняшка. материал (старшая группа) Кружок для детей Вкусняшка. материал (старшая группа) 126
Мое портфолио материал Мое портфолио материал 50
Дидактическая игра Многофункциональная сенсорная Гусеница презентация к уроку (младшая группа) Дидактическая игра Многофункциональная сенсорная Гусеница презентация к уроку (младшая группа) 58
День Матери 2015 год презентация к уроку (младшая, средняя группа) День Матери 2015 год презентация к уроку (младшая, средняя группа) 135
2 Kap2 2 Kap2 97
Безопасность детей на дороге план-конспект занятия (старшая группа) по теме Безопасность детей на дороге план-конспект занятия (старшая группа) по теме 139
Мордовская кухня Мордовская кухня 287
Адаптация ребенка в детском саду. презентация к занятию (младшая группа) по теме Адаптация ребенка в детском саду. презентация к занятию (младшая группа) по теме 120
Презентация Малые формы на территории доу презентация Презентация Малые формы на территории доу презентация 113