- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Основные теоремы
Содержание
- 2. 1. Теорема сложения вероятностей Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:. (1)
- 3. Докажем теорему сложения вероятностей для схемы случаев.
- 4. Обобщим теорему сложения на случай трех событий.
- 5. методом полной индукции обобщим теорему сложения на
- 6. ПустьТогда Но так как для n событий мы считаем теорему уже доказанной, тоСледовательночто и требовалось доказать
- 7. Следствия теоремыСледствие 1. Если события образуют полную группу
- 8. Определение: Противоположными событиями называются два несовместных события,
- 10. Пример 2. В урне 10 белых, 15
- 11. Пример 3. Круговая мишень (рис. ) состоит
- 12. Вероятность суммы двух совместимых событий выражается формулойВ справедливости формулы можно наглядно убедиться
- 13. Теорема умножения вероятностей Определение: Событие А называется независимым
- 14. Пример: Определить зависимы события или нет1) Опыт
- 16. Теорема: Вероятность произведения двух событий равна произведению
- 17. Доказательство:Докажем для схемы случаев. Пусть возможные исходы
- 18. Вычислим , условную вероятность события B в предположении, что A имело место.
- 19. при применении теоремы умножения безразлично, какое из событий и считать первым, а какое вторым,
- 21. Из следствия 1 вытекает, что зависимость или
- 22. Следствие 2. Вероятность произведения двух независимых событий
- 23. Скачать презентацию
- 24. Похожие презентации
1. Теорема сложения вероятностей Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:. (1)






















Слайд 2
1. Теорема сложения вероятностей
Вероятность суммы двух несовместимых событий
равна сумме вероятностей этих событий:
Слайд 3 Докажем теорему сложения вероятностей для схемы случаев. Пусть
возможные исходы опыта сводятся к совокупности случаев, которые мы
для наглядности изобразим в виде n точек:Предположим, что m из этих случаев благоприятны событию A,
а – n событию B.
Тогда
Так как события А и В несовместимы, то нет таких случаев, которые благоприятны и А, и В вместе. Следовательно, событию A и В благоприятны m+n случаев и
Подставляя полученные выражения в формулу (1), получим тождество.
Теорема доказана.
Слайд 4
Обобщим теорему сложения на случай трех событий.
Обозначая
событие А+В буквой D , и присоединяя к сумме еще одно событие C,
легко доказать, что:
Слайд 5
методом полной индукции обобщим теорему сложения на произвольное
число несовместных событий.
1. предположим, что она справедлива для n
событий:2. докажем, что она будет справедлива для n+1 событий:
Слайд 6
Пусть
Тогда
Но так как для n событий мы
считаем теорему уже доказанной, то
Следовательно
что и требовалось доказать
Слайд 7
Следствия теоремы
Следствие 1. Если события образуют полную группу несовместных
событий, то сумма их вероятностей равна единице:
Доказательство:
Так как события образуют
полную группу, то появление хотя бы одного из них – достоверное событие:Так как они несовместные события, то к ним применима теорема сложения вероятностей
Следовательно
что и требовалось доказать
Слайд 8 Определение: Противоположными событиями называются два несовместных события, образующих
полную группу.(А)
Следствие 2. Сумма вероятностей противоположных событий равна единице:
Это
следствие есть частный случай следствия 1Слайд 10 Пример 2. В урне 10 белых, 15 черных,
20 синих и 25 красных шаров. Вынули один шар.
Найти вероятность того, что вынутый шар а) синий или черный; б) белый, черный или синий.Решение. Обозначим следующие события:
Б – вынули белый шар, ;
Ч – вынули черный шар, ;
С – вынули синий шар, ;
К – вынули красный шар, .
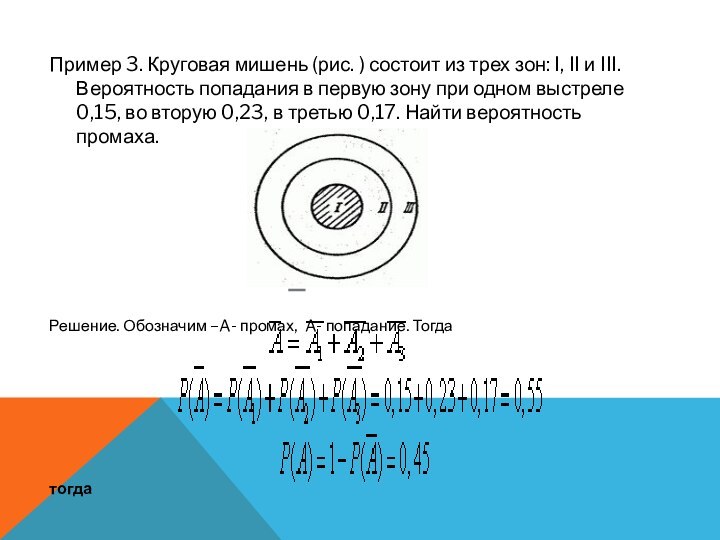
Слайд 11 Пример 3. Круговая мишень (рис. ) состоит из
трех зон: I, II и III. Вероятность попадания в
первую зону при одном выстреле 0,15, во вторую 0,23, в третью 0,17. Найти вероятность промаха.Решение. Обозначим –A- промах, A- попадание. Тогда
тогда
Слайд 12
Вероятность суммы двух совместимых событий выражается формулой
В справедливости
формулы можно наглядно убедиться
Слайд 13
Теорема умножения вероятностей
Определение: Событие А называется независимым от события В, если
вероятность события А не зависит от того, произошло событие В или нет.
Определение:
Событие А называется зависимым от события В , если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Слайд 14
Пример: Определить зависимы события или нет
1) Опыт состоит
в бросании двух монет; рассматриваются события:
А– появление герба на
первой монете,В – появление герба на второй монете.
2) В урне два белых шара и один черный; два лица вынимают из урны по одному шару; рассматриваются события:
А – появление белого шара у 1-го лица,
В– появление белого шара у 2-го лица.
Вероятность события А до того, как известно что-либо о событии В , равна 2/3.
Если стало известно, что событие В произошло, то вероятность события А становится равной ½, из чего заключаем, что событие зависит от события .
Слайд 16 Теорема: Вероятность произведения двух событий равна произведению вероятностей
одного из них на условную вероятность другого, вычисленную при
условии, что первое имело место:(2)
Слайд 17
Доказательство:
Докажем для схемы случаев. Пусть возможные исходы опыта
сводятся к n случаям, которые мы для наглядности изобразим в
виде точек:Предположим, что событию A благоприятны m случаев, а событию B благоприятны k случаев. Так как мы не предполагали события A и B несовместными, то вообще существуют случаи, благоприятные и событию A, и событию B одновременно. Пусть число таких случаев-l .
Тогда
Слайд 18
Вычислим , условную вероятность события B в предположении, что A имело место.
Если
известно, что событие A произошло, то из ранее возможных n случаев остаются возможными
только те m , которые благоприятствовали событию A. Из них l случаев благоприятны событию B.Следовательно,
Подставляя полученные выражения и в формулу (2), получим тождество.
Теорема доказана.
Слайд 19 при применении теоремы умножения безразлично, какое из событий и считать
первым, а какое вторым,
Слайд 21 Из следствия 1 вытекает, что зависимость или независимость
событий всегда взаимны.
Определение: Два события называются независимыми, если
появление одного из них не изменяет вероятности появления другого.Понятие независимости событий может быть распространено на случай произвольного числа событий. Несколько событий называются независимыми, если любое из них не зависит от любой совокупности остальных.