Презентация на тему План работы:

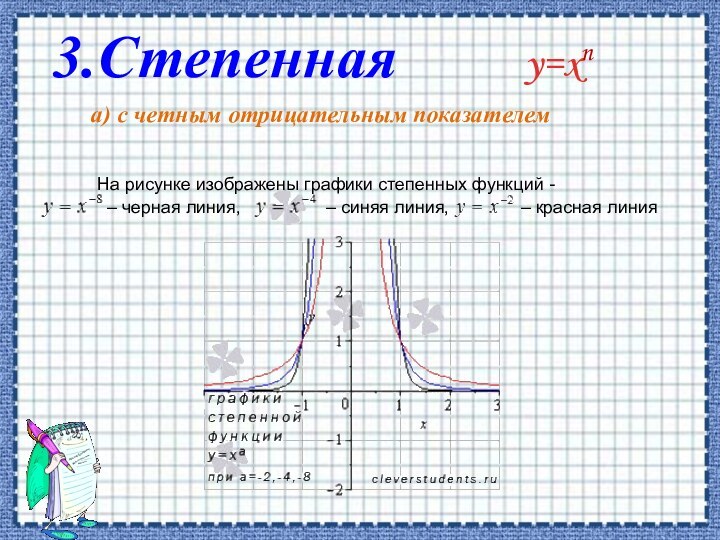
Степенная:
а) с четным отрицательным показателем
б) с нечетным отрицательным показателем
в)

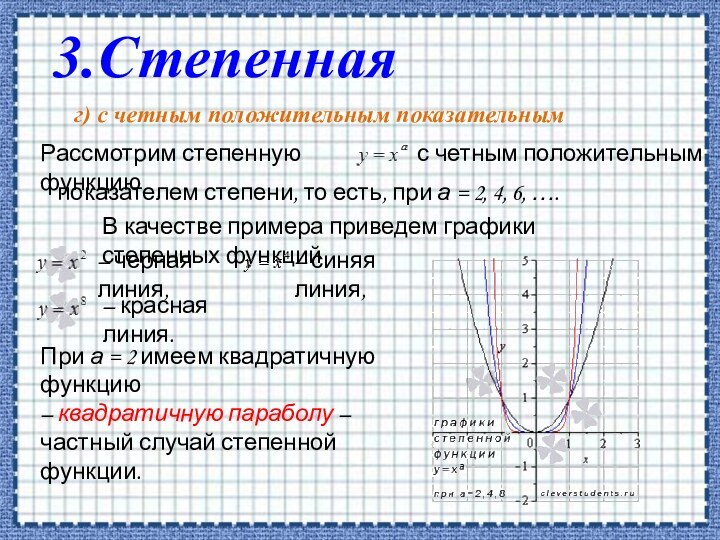
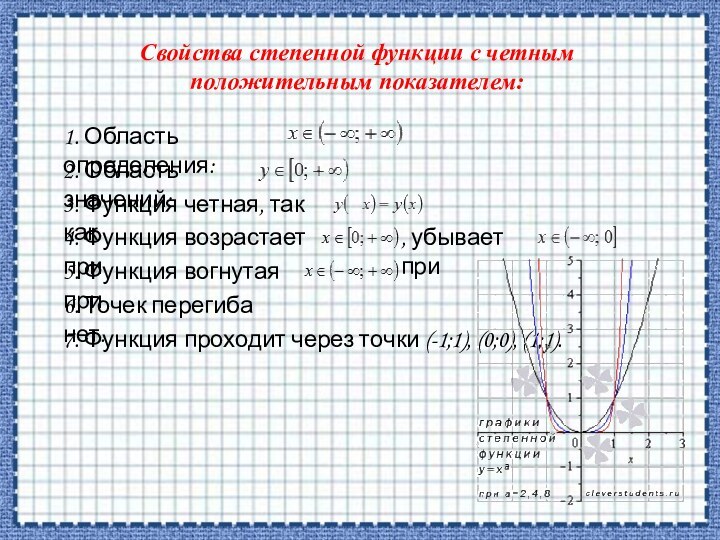
г) с четным положительным показателем

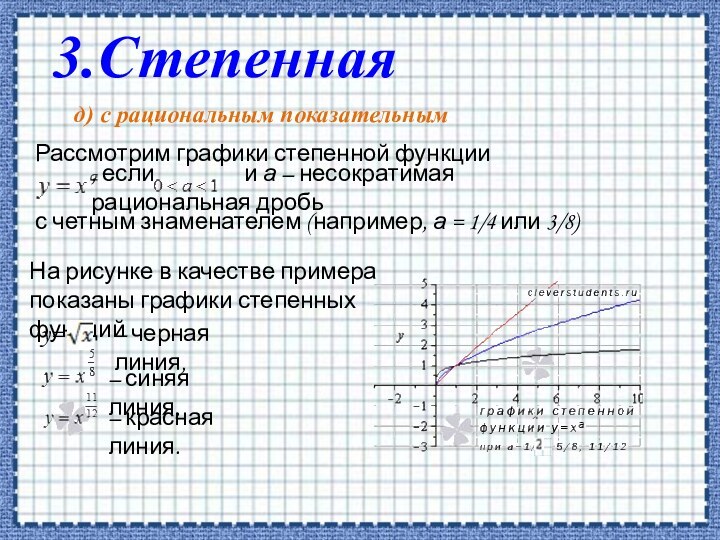
д) с рациональным показателем

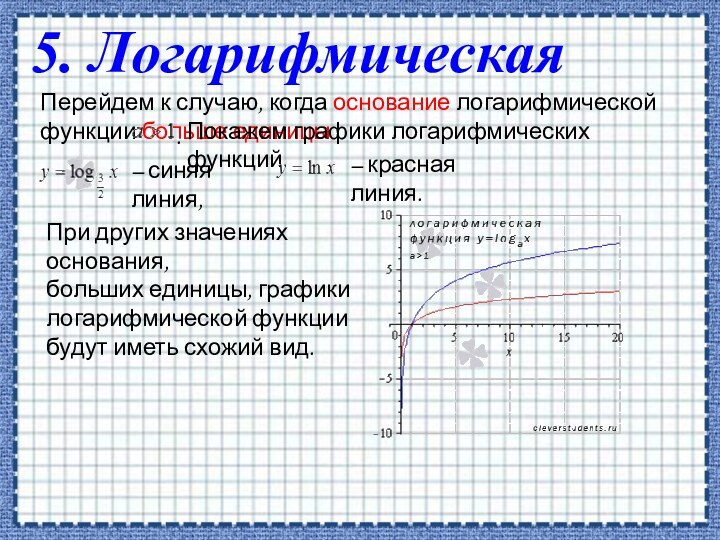
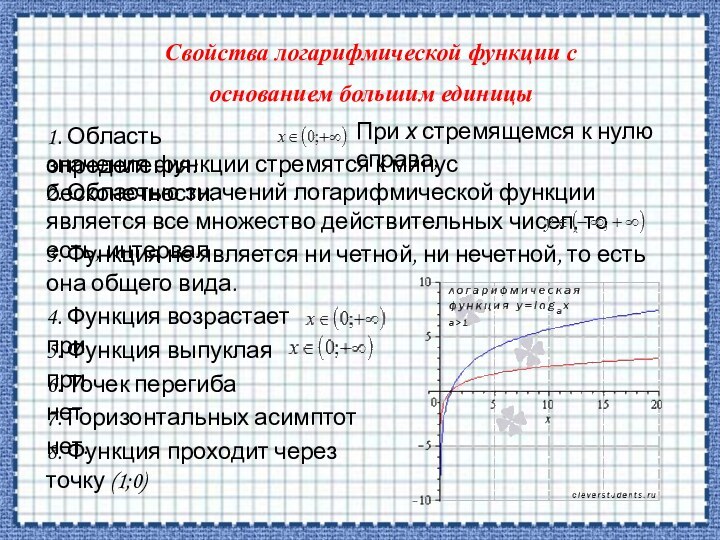
5. Логарифмическая

6. Тригонометрические:

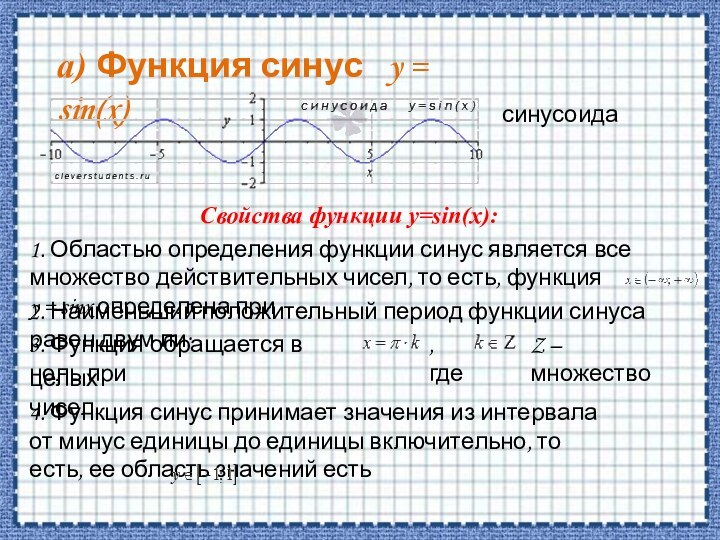
a) y=sin(x)

б) y=cos(x)

в) y=ctg(x)

г) y=tg(x)

7. Обратные тригонометрические:

a) y=arcsin(x)

б) y=arccos(x)

в) y=arcctg(x)

г) y=arctg(x)

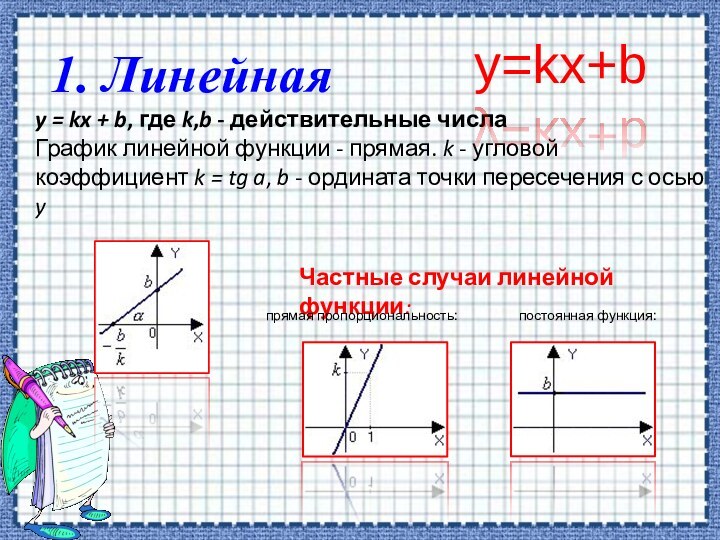
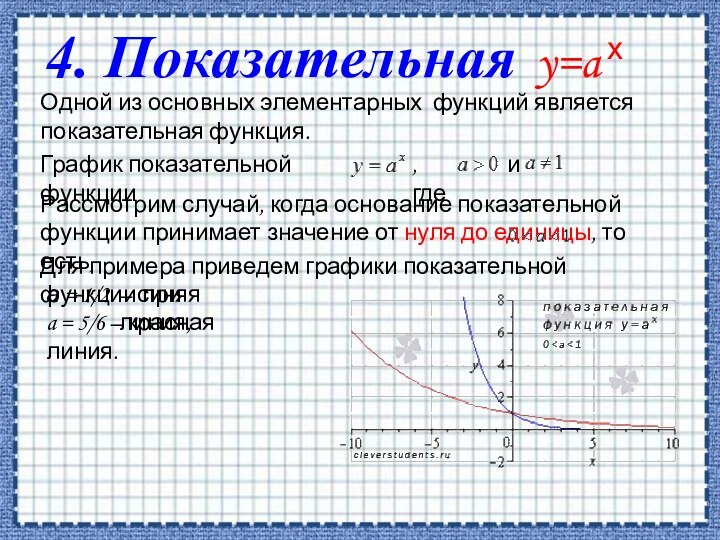
4. Показательная

где k,b - действительные числа График линейной функции -

Частные случаи линейной функции:

прямая пропорциональность:

постоянная функция:

y=kx+b

= kх. график - прямая, проходящая через начало координат
Свойства

1) Область определения - множество R

2) Область значений - множество R, если k
не равно 0, а если к =0, то число b

3) При к не равно 0, функция ни парная ни непарная; если к =0, то функция парная; если b =0, то функция непарная

4) При к>0 функция возрастает, при к <0 функция убывает, при к =0 постоянная

5) Функция не имеет экстремумов

6) График - прямая, не проходящая через начало координат

где a не равно График квадратичной функции - парабола. Свойства

a > 0, D > 0

a > 0, D = 0

a > 0, D < 0

Графиком этой функции является парабола

0, D = 0
a < 0, D < 0

при а > 0    [-D/(4a); ∞)
при а

при b =  0     функция четная при b ≠ 0 
 функция не является ни четной, ни нечетной

при D > 0      два нуля:

при D = 0      один нуль функции:

при D < 0     нулей функции нет

Свойства квадратичной функции:

то    
2) если, а > 0, D = 0, то  
3)

4) если а < 0, D > 0, то

5) если а < 0, D = 0, то  

6) если а < 0, D < 0, то

Промежутки знакопостоянства

при а = -2, -4, -6, …
y=xn


На

определения:
2. Область значений:
3. Функция четная, так как
4. Функция

убывает при

5. Функция вогнутая при

6. Точек перегиба нет.

7.Горизонтальной асимптотой является прямая y = 0

8. Функция проходит через точки (-1;1), (1;1).

при а = -1, -3, -5,…
На рисунке

– красная линия,

– зеленая линия.

При а = -1 имеем обратную пропорциональность (гиперболу) - частный случай степенной функции.

3.Степенная

определения:
2. Область значений:
3. Функция нечетная, так как
4. Функция

5. Функция выпуклая при

и вогнутая при

6. Точек перегиба нет.

7. Горизонтальной асимптотой является прямая y = 0

8. Функция проходит через точки (-1;-1), (1;1).

этой функции является
прямая
1
1
y=1
y
x
0
Свойства:
1. Область определения : y=R
2. Область

3. Функция не возрастает и не убывает

4.Функция не имеет экстремумов

5. График не проходит через начало координат

есть, при а = 2, 4, 6, ….
В

– черная линия,

– синяя линия,

– красная линия.

При а = 2 имеем квадратичную функцию
– квадратичную параболу –
частный случай степенной функции.

г) с четным положительным показательным

определения:
2. Область значений:
.
3. Функция четная, так

4. Функция возрастает при

, убывает при

5. Функция вогнутая при

6. Точек перегиба нет.

7. Функция проходит через точки (-1;1), (0;0), (1;1).

функции
, если

с четным знаменателем (например, а = 1/4 или 3/8)

На рисунке в качестве примера показаны графики степенных функций

y=

– синяя линия,

– красная линия.

– черная линия,

меньшим единицы:
1. Область определения:
2. Область значений:
3. Функция не является

4. Функция возрастает при

5. Функция выпуклая при

6. Точек перегиба нет.

7. Функция проходит через точки (0;0), (1;1).

функция.
График показательной функции
, где
и
Рассмотрим случай, когда основание

Для примера приведем графики показательной функции при

а = 1/2

– синяя линия,

a = 5/6 – красная линия.

y=a х

показательной функции является все множество действительных чисел:
2. Область значений:
3.

4. Показательная функция, основание которой меньше единицы, убывает на всей области определения.

5. Функция вогнутая при

6. Точек перегиба нет.

7. Горизонтальной асимптотой является прямая y = 0 при х стремящемся к плюс бесконечности.

8. Функция проходит через точку (0;1).

,
Логарифмическая функция определена лишь
для положительных значений аргумента, то есть,

График логарифмической функции принимает различный вид в зависимости от значения основания а.

Начнем со случая, когда

приведем графики логарифмической функции при

Для примера

а = 1/2

– синяя линия,

a = 5/6 – красная линия.

При других значениях основания, не
превосходящих единицы, графики
логарифмической функции будут иметь схожий
вид.

Область определения логарифмической функции:
при х стремящемся к нулю

2. Область значений:

3. Функция не является ни четной, ни нечетной, то есть она общего вида.

4. Логарифмическая функция убывает на всей области определения.

5. Функция вогнутая при

6. Точек перегиба нет.

7. Горизонтальных асимптот нет.

8. Функция проходит через точку (1;0).

больше единицы
Покажем графики логарифмических функций
.
– синяя линия,
– красная

При других значениях основания,
больших единицы, графики
логарифмической функции
будут иметь схожий вид.

х стремящемся к нулю справа,
значения функции стремятся к

2. Областью значений логарифмической функции является все множество действительных чисел, то есть, интервал

3. Функция не является ни четной, ни нечетной, то есть она общего вида.

4. Функция возрастает при

5. Функция выпуклая при

6. Точек перегиба нет

7. Горизонтальных асимптот нет.

8. Функция проходит через точку (1;0)

тангенс и котангенс) относятся к основным элементарным функциям.
У тригонометрических

где T - период),

поэтому, в список свойств тригонометрических

функций добавлен пункт «наименьший положительный период».

Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.

y=sin(x):
1. Областью определения функции синус является все множество действительных

2. Наименьший положительный период функции синуса равен двум пи:

3. Функция обращается в ноль при

,где

Z – множество

целых чисел.

4. Функция синус принимает значения из интервала от минус единицы до единицы включительно, то есть, ее область значений есть

нечетная, так как
6. Функция убывает при
,возрастает при
7. Функция

локальные минимумы в точках

8. Функция y = sinx вогнутая при

выпуклая при

9. Координаты точек перегиба

10. Асимптот нет.

данной функции
Свойства функции y=cos(x):
1. Область определения функции косинус:
2. Наименьший

3. Функция обращается в ноль при

, где

Z – множество
целых чисел.

4. Область значений функции косинус представляет интервал от минус единицы до единицы включительно:

5. Функция косинус - четная, так как

,возрастает при
7. Функция y = cosx имеет локальные максимумы в

локальные минимумы в точках

8. Функция вогнутая при

,выпуклая при

9. Координаты точек перегиба

10. Асимптот нет.

график функции тангенс (его называют "тангенсоида"):

Наименьший положительный период функции тангенс
3. Функция обращается в

, где

, Z – множество
целых чисел.

4.Область значений функции y = tgx:

5. Функция тангенс - нечетная, так как

6. Функция возрастает при

7. Функция вогнутая при

,выпуклая при

8. Координаты точек перегиба

9. Наклонных и горизонтальных асимптот нет.

график функции котангенс (его называют "котангенсоида"):

котангенс:
, где
2. Наименьший положительный период функции y = ctgx равен

3. Функция обращается в ноль при

, где

4. Область значений функции котангенс:

5. Функция нечетная, так как

6. Функция y = ctgx убывает при

7. Функция котангенс вогнутая при

,выпуклая при

8. Координаты точек перегиба

9. Наклонных и горизонтальных асимптот нет.

= arcsin(x)

арксинус является интервал от минус единицы до единицы включительно:

2. Область значений функции y = arcsin(x):

3. Функция арксинус - нечетная, так как

4. Функция y = arcsin(x) возрастает на всей области определения, то есть, при

5. Функция вогнутая при

, выпуклая при

6. Точка перегиба (0; 0), она же ноль функции

7. Асимптот нет.

функции арккосинус:
2. Область значений функции y = arccos(x):
3. Функция не

4. Функция арккосинус убывает на всей области определения, то есть, при

5. Функция вогнутая при

, выпуклая при

6. Точка перегиба

7. Асимптот нет.

arctg(x)

y = arctg(x):
2.Область значений функции арктангенс:
3. Функция арктангенс - нечетная,

4. Функция возрастает на всей области определения, то есть, при

5. Функция арктангенс вогнутая при

, выпуклая при

6. Точка перегиба (0; 0), она же ноль функции.

7. Горизонтальными асимптотами являются прямые

при

и

при

На чертеже они показаны зеленым цветом.

арккотангенс является все множество действительных чисел:
2. Область значений функции

3. Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.

4. Функция убывает на всей области определения, то есть, при

5. Функция вогнутая при

, выпуклая при

6. Точка перегиба

7. Горизонтальными асимптотами являются прямые

при

(на чертеже показана зеленым цветом) и y = 0 при