- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Подготовка к ЕГЭ. Решение задач С2.
Содержание
- 2. Типы задач С2Расстояние между двумя точкамиРасстояние от точки до плоскостиУгол между прямой и плоскостьюУгол между плоскостями
- 3. Расстояние между двумя точками Пусть точки
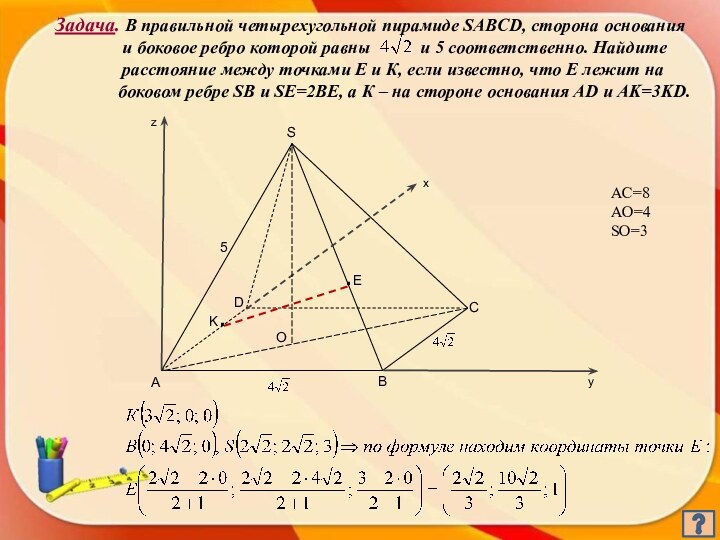
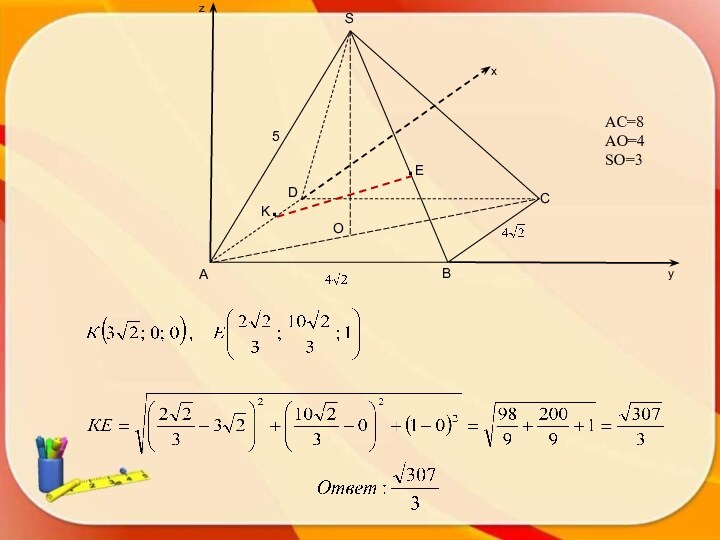
- 4. Задача. В правильной четырехугольной пирамиде SABCD, сторона
- 5. AC=8AO=4SO=3
- 6. Расстояние от точки до плоскостиКоординатный метод
- 7. Задача (ЕГЭ, 2012). В правильной треугольной призме
- 8. Угол между прямой и плоскостьюВекторно - координатный
- 9. Задача. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона
- 10. Угол между плоскостямиВекторно - координатный метод
- 11. Задача (ЕГЭ, 2012). В правильной четырёхугольной призме
- 12. Спасибо за внимание!
- 13. Пусть точки
- 14. Расстояние от точки до плоскостиКоординатный метод
- 15. Угол между прямой и плоскостьюВекторно - координатный
- 16. Скачать презентацию
- 17. Похожие презентации
Типы задач С2Расстояние между двумя точкамиРасстояние от точки до плоскостиУгол между прямой и плоскостьюУгол между плоскостями














Слайд 3
Расстояние между двумя точками
Пусть точки
- концы отрезка АВ. Тогда внутренняя точка С отрезка АВ такая, что АС:СВ=k, имеет координаты
Слайд 4
Задача. В правильной четырехугольной пирамиде SABCD, сторона основания
и боковое
ребро которой равны и 5 соответственно. Найдитерасстояние между точками Е и К, если известно, что Е лежит на
боковом ребре SB и SE=2BE, а К – на стороне основания AD и AK=3KD.
А
В
С
D
S
K.
.E
z
y
x
5
AC=8
AO=4
SO=3
O
Слайд 6
Расстояние от точки до плоскости
Координатный метод
Расстояние
от точки
заданной уравнением ax+by+cz+d=0, можно вычислить по формулеСлайд 7 Задача (ЕГЭ, 2012). В правильной треугольной призме ABCA1B1C1
стороны
основания равны 2, боковые рёбра равны 3, точка D – середина ребра CC1. Найдите расстояние от вершины
С до плоскости ADB1.
А
А1
В
В1
С
С1
z
y
x
. D
2
3
О
Решение:
Подставим координаты точек в уравнение плоскости ax+by+cz+d=0,
Вычислим расстояние от точки С до плоскости ADB1 по формуле:
Слайд 8
Угол между прямой и плоскостью
Векторно - координатный метод
Угол между прямой ℓ и плоскостью α можно
вычислить по формуле
Слайд 9
Задача. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона
основания равна 3,
а высота равна 1. Найдите угол между прямой F1B1и плоскостью AF1C1.
Решение:
А
А1
В
В1
С
С1
D
E
F
D1
E1
F1
y
x
z
3
1
Слайд 10
Угол между плоскостями
Векторно - координатный метод
Задачу
о нахождении угла между плоскостями α и β, заданными
в прямоугольной системе координат уравнениями p1x+q1y+r1z+d1=0 и p2x+q2y+r2z+d2=0 соответственно, удобнее свести к задаче о нахождении угла между векторами их нормалейСлайд 11 Задача (ЕГЭ, 2012). В правильной четырёхугольной призме ABCDA1B1C1D1
На ребре АА1 отмечена точка Е так, что АЕ:ЕА1=3:2.
Найдите угол между плоскостями АВС и BED1.
А
А1
В
В1
С
С1
D
D1
E .
y
x
z
2
5
Решение:
Составим уравнение плоскости BED1.
В(2;0;0), Е(0;0;3), D1(0;2;5)
Подставим координаты точек в уравнение плоскости ax+by+cz+d=0,
Т. к. ось Аz перпендикулярна плоскости основания, то нормальный вектор плоскости АВС имеет координаты
Слайд 13 Пусть точки
- концы отрезка АВ. Тогда внутренняя точка С отрезка АВ такая, что АС:СВ=k, имеет координаты
Расстояние между двумя точками