Слайд 2
1. Понятие вариации.
Различие индивидуальных значений признака внутри изучаемой
совокупности называется вариацией признака. Вариация возникает в результате того,
что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов.
.
Вариация
колеблемость величины признака у отдельных единиц совокупности под влиянием различных факторов, как систематических, так и случайных.
- это
Слайд 3
Систематические факторы- действуют постоянно, являются
существенными и проявляются в вариации закономерно.
Случайные
факторы- вносят хаотичность в изменение значений признака.
Вариацию под влиянием случайных факторов называют случайной вариацией, а под влиянием систематических факторов - систематической вариацией.
Общая вариация учитывает влияние как систематических, так и случайных факторов.
Слайд 4
Для изучения вариации значений признака
недостаточно знать только среднюю величину признака.
Средняя
величина не показывает строения совокупности, не дает представления о том, как отдельные значения изучаемого признака группируются вокруг своей средней величины.
В некоторых случаях отдельные значения признака близко примыкают к средней и мало от нее отличаются. В таких случаях средняя хорошо представляет всю совокупность, т.е . будет типичной.
В других случаях, отдельные значения признака совокупности далеко отстоят от средней, тогда средняя плохо представляет всю совокупность.
Поэтому необходимо знать и разброс отдельных единиц по отношению к среднему значению.
Слайд 5
Возникает необходимость
измерять вариацию признака в совокупностях. Для этой
цели вводится ряд обобщающих показателей вариации.
вариации – это разность между максимальным
и минимальным значением исследуемого признака в совокупности.
R= Xmax-Xmin
2. Среднее линейное отклонение – это средняя арифметическая абсолютных значений отклонений вариантов от их средней величины:
- простая при несгруппированных данных
- взвешенная при сгруппированных данных
квадратическое отклонение (называется стандартным отклонением) является наиболее
совершенной характеристикой вариации признака:
- простая форма
- взвешенная форма
Слайд 9
Среднее квадратическое отклонение - это
обобщающая характеристика размеров вариации признака в совокуп-ности, оно показывает,
на сколько в среднем отклоняются конкретные варианты признака от среднего значения, является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и признак, поэтому экономически хорошо интерпретируется.
Сопоставление средних отклонений – квадратического и линейного позволяет сделать вывод об устойчивости индивидуальных значений признака, т.е. об отсутствии среди них «аномальных» значений вариантов.
В условиях симметричного и нормального, а также близких к ним распределений, между показателями и имеют место равенства
= 1,25 , = 0,8.
Слайд 10
Отношение показателей
и может служить индикатором устойчивости данных:
если > 0,8, то значения признака неустойчивы, в них имеются «аномальные» выбросы.
Показатель вариаци является основной абсолютной мерой вариации. Он широко используется в выборочных наблюдениях при установлении границ однородности совокупности, при установлении формы кривой распределения и др.
Слайд 11
По значениям показателей
и можно определить границы диапазонов рассеяния значений
признака относительно средней , т.е. установить, какая доля значений признака попадает в тот или иной диапазон отклонений от .
В нормально распределенных и близких к ним рядах вероятностные оценки диапазонов рассеяния значений признака таковы:
68,3% войдет в диапазон ( );
95,4% попадет в диапазон ( );
99,7% появится в диапазон ( ).
Данное соотношение известно как правило «трех сигм».
По значениям и σ, основываясь на правиле «трех сигм», можно точно оценить границы всех трех диапазонов рассеяния признака и определить, сколько значений Хi попадает в каждый из диапазонов.
Дисперсия - это квадрат среднего квадратического отклонения:
- простая
- взвешенная
.
Формулу можно преобразовать:
Слайд 13
Пример 1. Имеются данные о товарообороте магазинов
района. Необходимо рассчитать характеристики ряда распределения.
1.
2.
Слайд 14
Дисперсия альтернативного признака
В ряде случаев возникает необходимость в измерении дисперсии альтернативных
признаков, тех, которыми обладают одни единицы совокупности, и не обладают другие (брак продукции, ученая степень и др.).
Обозначим р –доля единиц совокупности, обладающая данным признаком и q – доля единиц, не обладающая данным признаком: р+q =1.
Альтернативный признак принимает всего два значения 0 и 1 с весами соответственно q и р.
Найдем среднее значение альтернативного признака:
Слайд 15
Дисперсия альтернативного признака:
Пример. На 10000 человек населения района
приходится 4500 мужчин и 5500 женщин.
Среднее квадратическое отклонение альтернативного
признака:
Пример. Известно, что 2% всех деталей бракованные. Найти дисперсию брака.
Среднеквадратическое отклонение доли брака будет
Слайд 16
Интенсивность вариации признака измеряется
относительными показателями.
Относительные показатели вводятся для
сравнительной оценки вариации совокупности по разным признакам или для сравнения вариаций нескольких совокупностей по одному и тому же признаку.
Эти показатели вычисляются как отношение абсолютных показателей вариации к средней величине.
Слайд 18
Коэффициент вариации V
выражается в процентах и вычисляется по формуле:
Величина V
оценивает интенсивность колебаний вариантов относительно их средней величины. Принята следующая оценочная шкала колеблемости признака:
0%40%< V≤60% - колеблемость средняя (умеренная);
V>60% - колеблемость значительная.
Для нормальных и близких к нормальному распределений показатель V служит индикатором однородности совокупности: V≤33%
Слайд 19
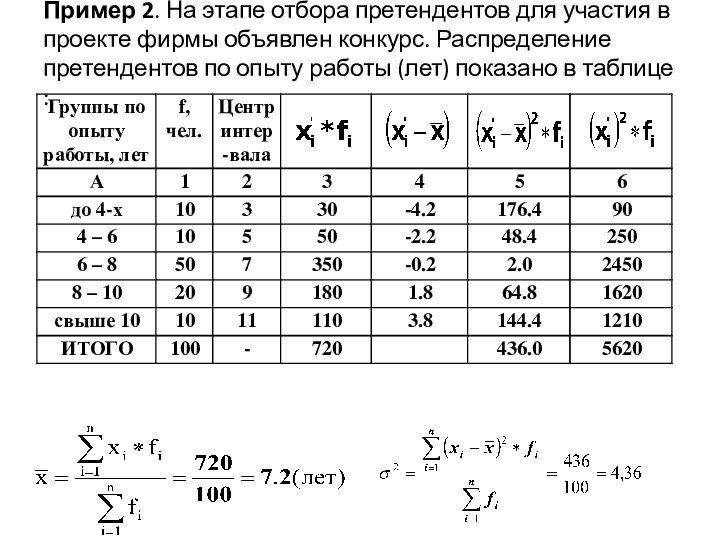
Пример 2. На этапе отбора претендентов для участия
в проекте фирмы объявлен конкурс. Распределение претендентов по опыту
работы (лет) показано в таблице :
дисперсий в совокупности, разделенной на
группы. Правило сложения дисперсии.
Вариация признака обусловлена различными факторами. Поэтому, изучая вариацию по всей совокупности в целом и рассчитав общую среднюю, невозможно определить влияние отдельных факторов на колеблемость индивидуальных значений признака.
Это можно сделать, если статистическую совокупность разбить на группы по какому-либо признаку-фактору. Тогда, наряду с изучением вариации признака по всей совокупности в целом, можно изучить вариацию для каждой из составляющих ее групп, а также вариацию между этими группами.
Слайд 21
Показатели вариации могут
быть использованы не только в анализе колеблемости признака, но
и для оценки влияния одного признака на вариацию другого признака, т.е. в анализе взаимосвязей между показателями.
Для такого анализа совокупность должна быть разбита на группы по факторному признаку. При этом используются три вида дисперсий - это общая дисперсия, дисперсия межгрупповая и внутригрупповая (средняя из внутригрупповых дисперсий).
Слайд 22
Обозначая факторный признак – Х,
результативный – У, дадим определение этих трех видов дисперсии.
Введем
обозначения:
1 гр.
1 г
n=n1+n2+…+nk;
k – количество групп;
– среднее значение результативного признака У в j-ой группе;
– общая средняя по всей совокупности;
n – число единиц совокупности.
характеризует вариацию признака во всей совокупности,
сложившуюся под влиянием всех факторов (систематических и случайных), обусловивших эту вариацию.
Межгрупповая дисперсия измеряет систематическую вариацию, которая обусловлена влиянием того признака-фактора Х, по которому произведена группировка. Такое воздействие фактора проявляется в отклонении групповых средних от общей средней.
Слайд 24
– групповые средние;
– общая средняя;
– численность единиц в
j-ой группе;
k – количество групп.
Внутригрупповая дисперсия оценивает вариацию признака, сложившуюся под влиянием других, не учитываемых в данном исследовании факторов, и не зависящую от группировочного фактора Х.
Слайд 25
yi – индивидуальные значения признака внутри группы;
– среднее значение признака в
группе с номером j;
nj – численность единиц в j-ой группе.
На основании внутригрупповых дисперсий всех групп , вычисляется средняя из внутригрупповых дисперсий:
Слайд 26
Правило сложения дисперсии :
Данное правило показывает связь
между различными видами дисперсий.
Это правило позволяет оценить влияние
группировочного признака на образование общей вариации.
Очевидно, чем больше доля межгрупповой дисперсии в общей, тем сильнее влияние группировочного Х признака на изучаемый результативный признак Y.
Слайд 27
В статистическом анализе широко
используется показатель , который называют эмпирическим
коэффициентом детерминации.
Он характеризует долю межгрупповой дисперсии в общей дисперсии .
Межгрупповая дисперсия обусловлена вариацией признака, положенного в основу группировки. Она показывает силу влияния факторного признака на образования общей вариации:
Эмпирический коэффициент детерминации показывает долю вариации результативного признака Y под влиянием вариации факторного признака Х.
между группировочным и результативным признаками оценивается показателем
, который называется эмпирическим корреля-ционным отношением.
Для качественной оценки тесноты связи на основе служит соотношение Чэддока:
Чем значение ближе к 1, тем теснее связь между признаками.
Слайд 29
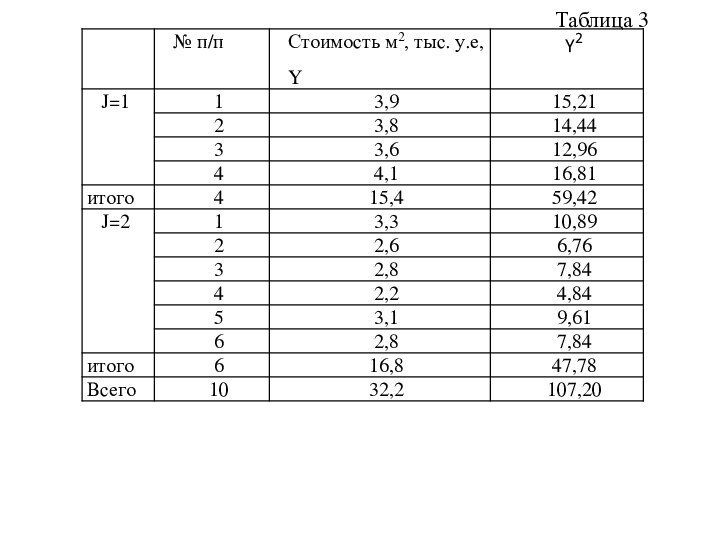
Пример 3.
Стоимость 1
кв.м общей площади в у.е. на рынке жилья для
двух групп домов приведена в таблице 3. При этом известно, что дома 1-ой группы находятся вблизи от станции метро, а дома 2-ой группы – на значительном расстоянии от станции метро.
Необходимо установить влияет ли местораспо-ложение домов на стоимость 1 кв.м общей площади.
Группировочный факторный признак Х – это качественный признак (расположение дома – близость к станции метро); результативный признак Y – стоимость 1 кв.м общей площади.
Слайд 31
1. Рассчитаем среднюю стоимость одного м2. жилья и
общую дисперсию по всей совокупности в целом:
2. Вычислим среднюю
стоимость одного м2 жилья и дисперсию для каждой группы домов.
Слайд 32
3.Определим величину межгрупповой дисперсии
4. Найдем
эмпирический коэффициент детерминации
6. Определим среднею из внутригрупповых дисперсий
5. Эмпирическое
корреляционное отношение
7. Найденные дисперсии в сумме дают общую дисперсию.
0,2646+0,0869=0,3515
Слайд 33
Правило сложения дисперсии для доли признака.
Рассмотренное правило сложения
дисперсий верно и для дисперсии доли признака.
Дисперсия альтернативного признака:
Средняя величина
Тогда внутригрупповая дисперсия доли :
где pi - доля изучаемого признака в i-ой группе.
Средняя из внутригрупповых дисперсий :
Слайд 34
Формула межгрупповой дисперсии имеет вид:
где ni - численность
единиц в отдельных группах;
- доля изучаемого признака во всей совокупности.
Доля признака в совокупности определяется по средней арифметической взвешенной:
Правило сложения дисперсий доли признака выражается соотношением:
Слайд 35
Пример 4. Данные удельного веса основных рабочих в
трех цехах фирмы представлены в таблице.
Определить общую, внутрицеховую и межцеховую дисперсии доли основных рабочих.
1. Определим долю основных рабочих в целом по фирме:
Слайд 36
2. Общая дисперсия доли основных рабочих по всей
фирме в целом равна:
3. Внутрицеховые дисперсии равны:
4. Средняя из
внутрицеховых дисперсий равна:
Слайд 37
5. Межцеховая дисперсия равна:
Проверка вычислений: 0,154
= 0,15 + 0,004.
Слайд 38
3.Характеристика закономерности рядов распределения.
Для обобщающей характеристики
особенностей формы распределения применяются кривые распределения, которые выражают графически
закономерность распределения единиц совокупности по величине варьирующего признака.
Различают эмпирические и теоретические кривые распределения.
Эмпирическая кривая распределения - это фактическая кривая распределения, полученная по данным наблюдения, в которой отражаются как общие, так и случайные условия, определяющие распределение.
Теоретическая кривая распределения - это кривая, выражающая общую закономерность данного типа распределения. При этом теоретическое распределение играет роль некоторой идеализированной модели эмпирического распределения, а сам процесс анализа вариационного ряда сводится к сопоставлению эмпирического и теоретического распределений..
Слайд 39
Кривые распределения могут быть
одно-, двух- и многовершинными.
Для однородных совокупностей
характерны одновершинные распределения. Многовершинность свидетельствует о неоднородности изучаемой совокупности. В этом случае необходимо сделать перегруппировку данных с целью получения однородных групп.
Кривые распределений бывают симметричными и асимметричными. В зависимости от того, какая ветвь кривой вытянута - правая или левая, различают правостороннюю или левостороннюю асимметрию.
Для симметричных распределений частоты любых двух вариантов, равноотстоящих от центра в обе стороны, равны между собой.
Слайд 40
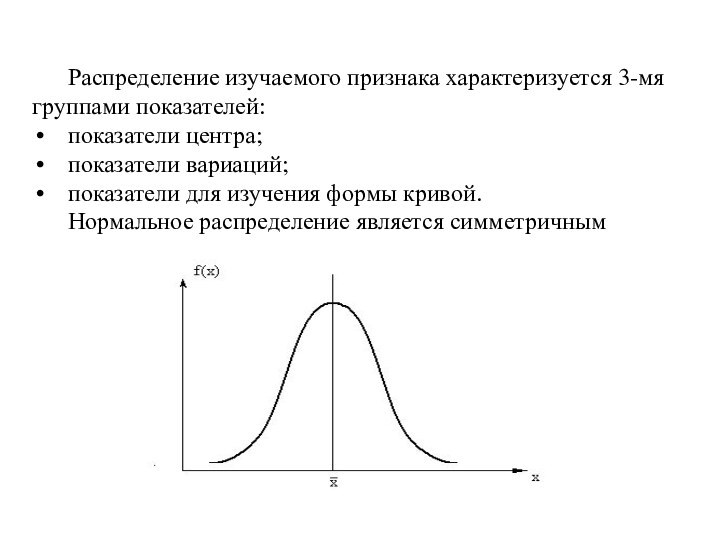
Распределение изучаемого признака характеризуется 3-мя группами показателей:
показатели центра;
показатели
вариаций;
показатели для изучения формы кривой.
Нормальное распределение является
симметричным
Слайд 41
Для симметричных распределений имеют место следующие
характеристики:
1.
2.
3.
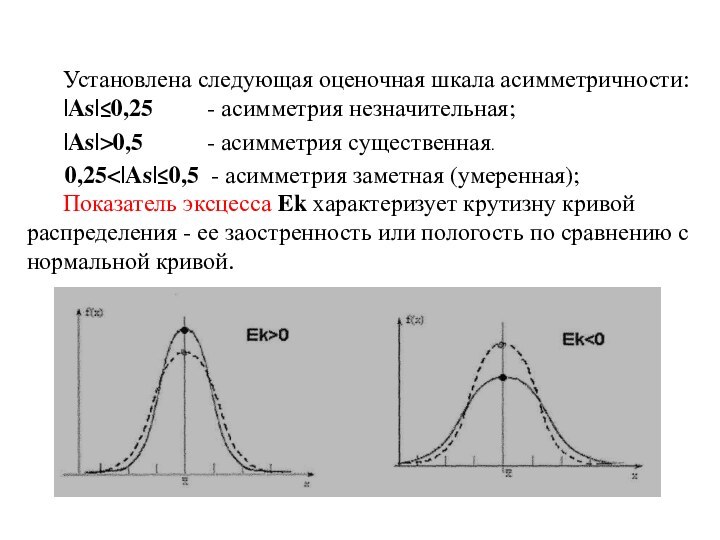
Показатель асимметрии As оценивают смещение ряда распределения влево или
вправо по отношению к оси симметрии нормального распределения.
В случае асимметричного распределения вершина кривой находится не в середине, а сдвинута либо влево, либо вправо.
Если эти соотношения нарушены, то это свидетельствует о наличии асимметрии распределения.
Слайд 42
Если вершина сдвинута влево, то правая часть кривой
оказывается длиннее левой т.е. имеет место правосторонняя асимметрия, характеризующаяся
неравенством
>Me>Mo.
Если же вершина кривой сдвинута вправо и левая часть оказывается длиннее правой, то асимметрия левосторонняя, для которой справедливо неравенство