- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Понятия, высказывания, умозаключения
Содержание
- 2. Имена и понятияОтношения между понятиямиПростые и сложные высказыванияКатегорические высказыванияСужденияВопросыУмозаключенияЗаключениеГлоссарийСписок использованной литературыПлан
- 3. Имеются многообразные имена, в частностипонятия, обозначающие отдельныепредметы и их множества.1. Имена и понятия
- 4. С помощью логических связок, подобных «есть», «некоторые…есть» и т.д. складываютсяРассужденияУмозаключенияВысказывания
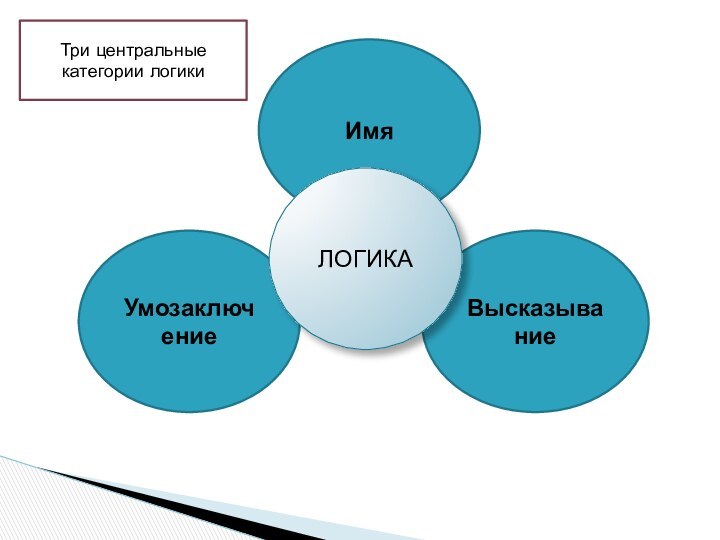
- 5. ИмяУмозаключениеВысказываниеЛОГИКАТри центральные категории логики
- 6. Имя – это выражение языка, обозначающее отдельный предмет или совокупность разных предметов.
- 7. слово «Цезарь» обозначает отдельныйпредмет – первого римского
- 8. обозначают один и только один предмет.Единичные именаНапример:
- 9. обозначают более чем один предмет.Общие именаНапример: «Человек» «Женщина» «Школьник» и т.п.
- 10. общее имя с относительно ясным иустойчивым содержанием,
- 11. Содержание понятия – совокупность техсвойств, которые присущи всем предметам,обозначаемым данным понятием и толькоим.2. Отношения между понятиями
- 12. Пример:Склероз – это, как известно, уплотнениекаких-либо органов,
- 13. Помимо содержания, или смысла, понятие имеет также объем
- 14. Объем понятия – совокупность, или класс,тех предметов, которые обладаютпризнаками, входящими в содержаниепонятия.
- 15. Например:в объем понятия «склероз» входят все случаи склеротического изменения органов, в частности склероз мозга.
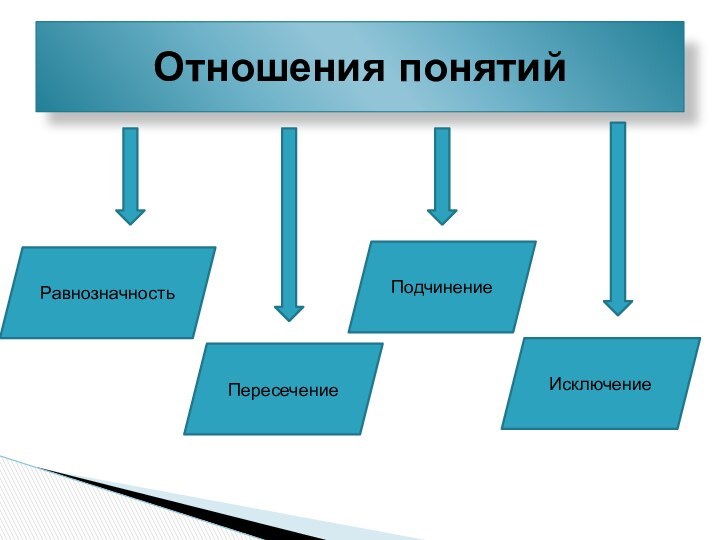
- 16. Отношения понятийРавнозначность Пересечение Подчинение Исключение
- 17. отношение между понятиями, объемыкоторых полностью совпадают.Равнозначность Например:Понятия
- 18. Равнозначностьозначает совпадениеобъемов двух понятий,но не их содержаний.Например:Объемы
- 19. Отношения междуобъемами понятийможно геометрическинаглядно представитьс помощью круговыхсхем. Они называются поимени русскогоматематика XVIIIв.Л.Эйлера «кругамиЭйлера».Л. Эйлер(1707 -1783)
- 20. S, PРавнозначность Отношения между двумя равнозначными понятиями
- 21. ПересечениеОтношение между понятиями, объемы которых частично совпадают.Например,
- 23. SPИсключениеИсключают друг друга понятия «трапеция» и «пятиугольник», «человек» и «планета», «белое» и «красное».
- 24. Высказывание – грамматически правильноепредложение, взятое вместе с
- 25. Истинностные значения высказываний:«Истина»«Ложь»
- 26. Из отдельных высказываний равнымиспособами можно строить новыевысказывания.Например,
- 27. Высказывание называется простым, если оно не включает
- 28. Способы построения высказываний:Отрицательное высказываниеУсловное высказывание
- 29. Состоит их исходного высказывания и отрицания, выражаемого
- 30. Соединение двух высказываний при помощислова «и» дает
- 32. В обычном языке два высказываниясоединяются союзом «и», когда они связанымежду собой по содержанию или смыслу.
- 33. Соединение двух высказываний с помощьюслова «или» дает дизъюнкцию этихвысказываний.Высказывания, образующие дизъюнкцию,называются «членами дизъюнкции».
- 34. Неисключающая дизъюнкцияОзначает, что одно из высказываний истинно,
- 35. Условное высказывание – сложное высказывание, формулируемое обычно
- 36. Например:«Если есть огонь, то есть дым»;«Если число делиться на 9, оно делится на 3» и т.п.
- 37. 4. Категорические высказыванияКатегорическое высказывание – это высказывание,
- 38. Например:В высказывании «Все динозавры вымерли»динозаврам предписывается признак
- 39. УтвердительныйОтрицательныйДва варианта высказываний, которые выражаются словами «все» и «некоторые»«S есть P» и «S не есть P»
- 40. Все S есть P – общеутвердительное высказывание;Некоторые
- 41. Например:Общеутвердительное: «Все рыбы есть позвоночные»;Частноутвердительное: «Некоторые книги
- 42. 5. СужденияСуждение представляет собой мысль, выражаемую высказыванием.
- 43. БессмысленноеОсмысленноеСуждение
- 44. Абсурд Абсурд – внутренне противоречивое выражениеНапример:«Космонавты долетели с Юпитера до Земли за три минуты»
- 45. Каждый язык имеет определенные правилапостроения сложных выражений
- 46. Например:Выражение «Если стол, то стул»бессмысленно, поскольку синтаксис
- 47. Понятие «осмысленность», подобно понятию«смысл», относится к семантике языка,описывающей отношение сказанного кдействительности.Семантические нарушения
- 48. Например:Предложение «Идет дождь» описываетопределенное событие, но высказывание«Если
- 49. Классификация суждений
- 50. 6. ВопросыВопрос – это выраженное в форме
- 51. Вопросы различаются по своей структуре ипо своим функциям.Классификация вопрсоовВопросВосполняющие(что – вопросы)Уточняющие (ли-вопросы)
- 52. Например:Уточняющий: «Верно ли, что Луна вращаетсявокруг Земли?»;Восполняющий: «Кто изобрел автомобиль?».
- 53. Вопросы необходимо ставить корректно.Вопрос нужно формулировать кратко
- 54. Ответы на вопрос
- 55. 7. УмозаключенияУмозаключение – логическая операция, в результате
- 56. УмозаключениеИндуктивноеДедуктивное
- 57. В основе дедуктивного умозаключения лежитлогический закон, в
- 58. В индуктивном умозаключении связь посылоки заключения опирается
- 59. Таким образом, с точки зрения
- 60. ГлоссарийЛогика – наука о законах и операциях
- 61. ГлоссарийПересечение - отношение между понятиями, объемы которых
- 62. ГлоссарийВопрос - это выраженное в форме вопросительного
- 63. Скачать презентацию
- 64. Похожие презентации
















































Слайд 2
Имена и понятия
Отношения между понятиями
Простые и сложные высказывания
Категорические
высказывания
Слайд 3
Имеются многообразные имена, в частности
понятия, обозначающие отдельные
предметы и
их множества.
1. Имена и понятия
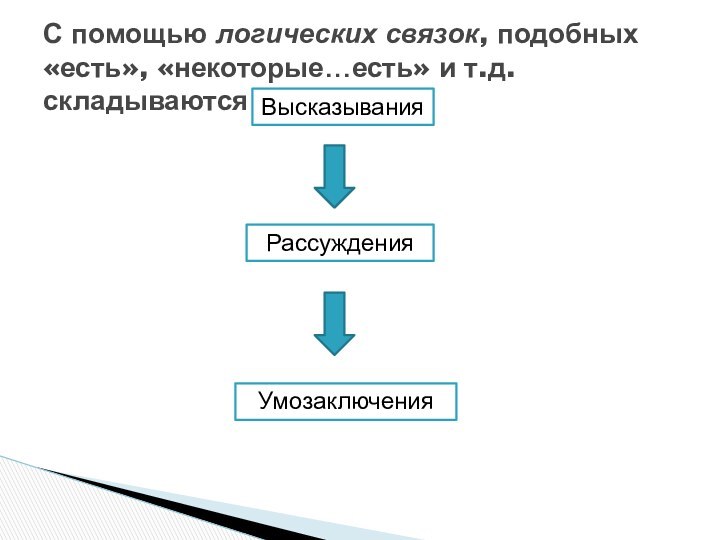
Слайд 4 С помощью логических связок, подобных «есть», «некоторые…есть» и
т.д. складываются
Рассуждения
Умозаключения
Высказывания
Слайд 6 Имя – это выражение языка, обозначающее отдельный предмет
или совокупность разных предметов.
Слайд 7
слово «Цезарь» обозначает отдельный
предмет – первого римского императора
Цезаря;
слово
«ученый» обозначает класс людей,
каждый из которых занят научными
исследованиями;
слово «черный»
может рассматриваться какобозначение класса черных предметов;
слово «дальше» – как обозначение
определенного отношения между
предметами.
Например:
Слайд 8
обозначают один и только один предмет.
Единичные имена
Например:
«Солнце»
– единственная звезда в Солнечной системе.
«Луна» – единственный
спутник Земли.
Слайд 9
обозначают более чем один предмет.
Общие имена
Например:
«Человек»
«Женщина»
«Школьник»
и т.п.
Слайд 10
общее имя с относительно ясным и
устойчивым содержанием, используемое
в
обычном языке или в языке науки.
Понятие
Например:
«Дом»
«Квадрат»
«Молекула»«Кислород»
«Атом»
Слайд 11
Содержание понятия – совокупность тех
свойств, которые присущи всем
предметам,
обозначаемым данным понятием и только
им.
2. Отношения между понятиями
Слайд 12
Пример:
Склероз – это, как известно, уплотнение
каких-либо органов, вызванное
гибелью
специфических для этих органов элементов
и заменой их соединительной тканью.
Перечисленные
свойства составляютсодержание понятия «склероз».
Они позволяют относительно любой
ситуации решить, можно ли назвать
происшедшие в органе изменения склерозом
или нет.
Слайд 14
Объем понятия – совокупность, или класс,
тех предметов, которые
обладают
признаками, входящими в содержание
понятия.
Слайд 15
Например:
в объем понятия «склероз» входят все случаи склеротического
изменения органов, в частности склероз мозга.
Слайд 17
отношение между понятиями, объемы
которых полностью совпадают.
Равнозначность
Например:
Понятия «квадрат»
и «равносторонний прямоугольник»: каждый квадрат является односторонним прямоугольником, и
наоборот.
Слайд 18
Равнозначность
означает совпадение
объемов двух понятий,
но не их содержаний.
Например:
Объемы понятий
«сын» и «внук» совпадают (каждый сын есть чей-то внук
и каждый внук – чей-то сын), но содержания различны.
Слайд 19
Отношения между
объемами понятий
можно геометрически
наглядно представить
с помощью круговых
схем.
Они
называются по
имени русского
математика XVIIIв.
Л.Эйлера «кругами
Эйлера».
Л. Эйлер
(1707 -1783)
Слайд 20
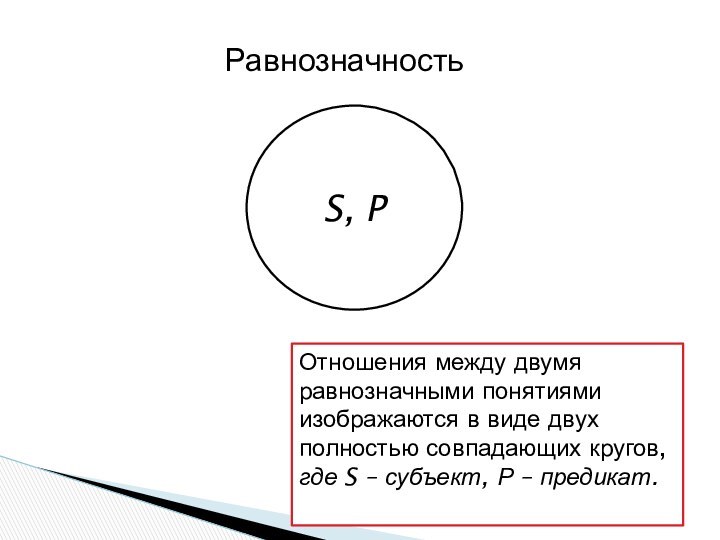
S, P
Равнозначность
Отношения между двумя равнозначными понятиями изображаются
в виде двух полностью совпадающих кругов, где S –
субъект, Р – предикат.
Слайд 21
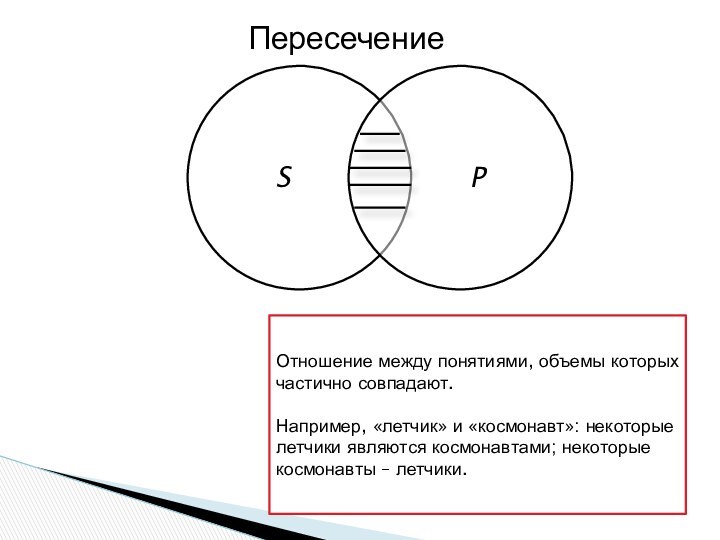
Пересечение
Отношение между понятиями, объемы которых частично совпадают.
Например, «летчик»
и «космонавт»: некоторые летчики являются космонавтами; некоторые космонавты –
летчики.Слайд 22
P
S
P
S
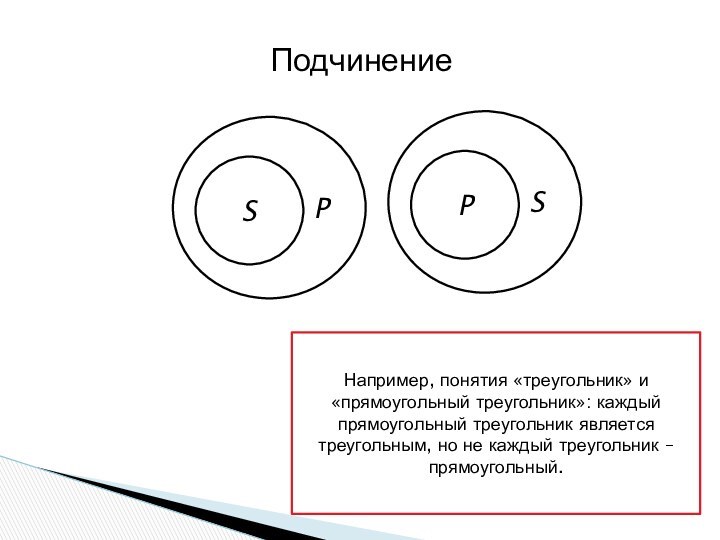
Подчинение
Например, понятия
«треугольник» и «прямоугольный треугольник»: каждый прямоугольный треугольник является треугольным, но не каждый треугольник – прямоугольный.
Слайд 23
S
P
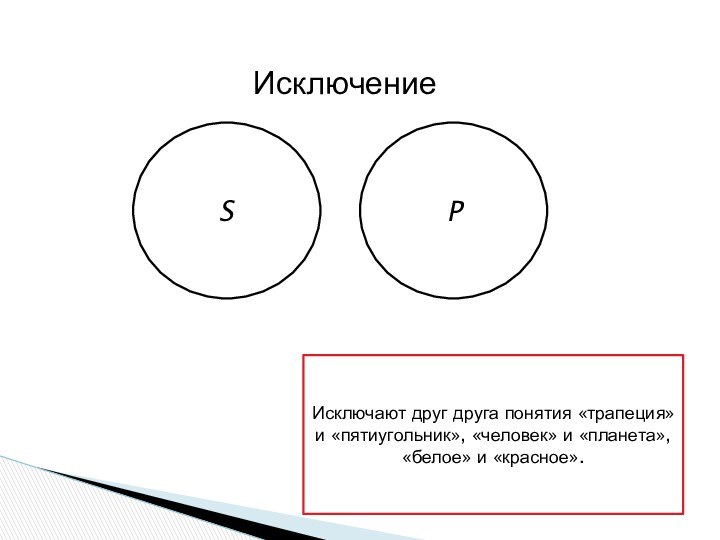
Исключение
Исключают друг друга понятия «трапеция» и «пятиугольник», «человек»
и «планета», «белое» и «красное».
Слайд 24
Высказывание – грамматически правильное
предложение, взятое вместе с выражаемым
им
смыслом (содержанием) и являющееся
истинным или ложным.
3. Простые и сложные
высказывания.
Слайд 26
Из отдельных высказываний равными
способами можно строить новые
высказывания.
Например, из
высказываний «Дует ветер» и
«Идет дождь» можно образовать более
сложное высказывание
«Дует ветер и идетдождь», «Либо дует ветер, либо идет дождь»,
«Если идет дождь, то дует ветер» и т.п.
Слайд 27 Высказывание называется простым, если оно не включает других
высказываний в качестве своих частей.
Высказывание называется сложным, если оно
получено с помощью логических связок из других более простых высказываний.Слайд 29 Состоит их исходного высказывания и отрицания, выражаемого обычно
словами «не», «неверно, что»;
Является сложным: включает в себя в
качестве своей части отличное от него высказывание (например, отрицанием высказывания «10 – четное число» является высказывание «10 не есть четное число»).Отрицательное высказывание
Слайд 30
Соединение двух высказываний при помощи
слова «и» дает сложное
высказывание,
называемое конъюнкцией.
Высказывания, соединяемые таким образом,
Называются «членами конъюнкции».
Например, если
высказывания «Стало жарко»и «Вчера было холодно» соединить таким
способом, получится конъюнкция «Сегодня
жарко и вчера было холодно».
Слайд 32
В обычном языке два высказывания
соединяются союзом «и», когда
они связаны
между собой по содержанию или смыслу.
Слайд 33
Соединение двух высказываний с помощью
слова «или» дает дизъюнкцию
этих
высказываний.
Высказывания, образующие дизъюнкцию,
называются «членами дизъюнкции».
Слайд 34
Неисключающая дизъюнкция
Означает, что одно из высказываний истинно, независимо
от того, истинны они оба или нет.
Исключающая
дизъюнкция
Означает, что одно
из высказываний истинно, а второе – ложно.Слайд 35 Условное высказывание – сложное высказывание, формулируемое обычно с
помощью связки «если…, то…» и устанавливающее, что одно событие,
состояние и т.п. является в том или ином смысле основанием или условием для другого.
Слайд 36
Например:
«Если есть огонь, то есть дым»;
«Если число делиться
на 9, оно делится на 3» и т.п.
Слайд 37
4. Категорические высказывания
Категорическое высказывание – это высказывание, в
котором утверждается или отрицается наличие какого-либо признака у всех
или некоторых предметов рассматриваемого класса.
Слайд 38
Например:
В высказывании «Все динозавры вымерли»
динозаврам предписывается признак «быть
вымершими».
В суждении «Некоторые
летали» способность летать предписывается
отдельным видам динозавров.
Слайд 39
Утвердительный
Отрицательный
Два варианта высказываний, которые выражаются словами «все» и
«некоторые»
«S есть P» и «S не есть P»
Слайд 40
Все S есть P – общеутвердительное высказывание;
Некоторые S
не есть P – частноутвердительное высказывание;
Все S не есть
P – общеотрицательное утверждение;Некоторые S не есть P – частноотрицательное высказывание.
4 вида категорических высказываний:
Слайд 41
Например:
Общеутвердительное: «Все рыбы есть позвоночные»;
Частноутвердительное: «Некоторые книги полезные»;
Общеотрицательные:
«Ни одно насекомое не есть позвоночное»;
Частноотрицательное: «Некоторые змеи не
имеют ядовитых зубов».
Слайд 44
Абсурд
Абсурд – внутренне противоречивое выражение
Например:
«Космонавты долетели с
Юпитера до Земли за три минуты»
Слайд 45
Каждый язык имеет определенные правила
построения сложных выражений из
простых,
правила синтаксиса.
Как и все правила, они могут нарушаться, и
это
ведет к самому простому и, как кажется,самому прозрачному типу бессмысленного.
Синтаксические нарушения
Слайд 46
Например:
Выражение «Если стол, то стул»
бессмысленно, поскольку синтаксис требует,
чтобы
во фразе с «если…, то…» на местах
многоточий стояли некоторые
утверждения,а не имена.
Слайд 47
Понятие «осмысленность», подобно понятию
«смысл», относится к семантике языка,
описывающей
отношение сказанного к
действительности.
Семантические нарушения
Слайд 48
Например:
Предложение «Идет дождь» описывает
определенное событие, но высказывание
«Если идет
дождь, то голова» ни к чему в
мире не приложимо
и являетсябессмысленным.
Слайд 50
6. Вопросы
Вопрос – это выраженное в форме вопросительного
предложения пожелание, направленное на развитие, уточнение или дополнение имеющегося
знания.
Слайд 51
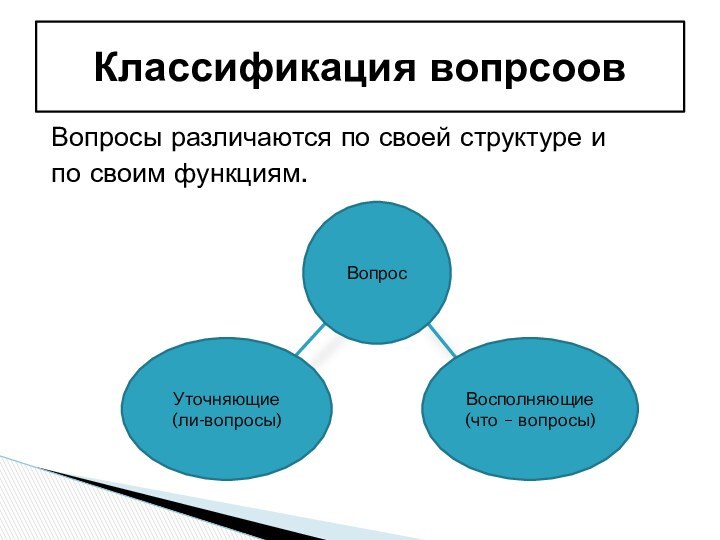
Вопросы различаются по своей структуре и
по своим функциям.
Классификация
вопрсоов
Вопрос
Восполняющие
(что – вопросы)
Уточняющие
(ли-вопросы)
Слайд 52
Например:
Уточняющий: «Верно ли, что Луна вращается
вокруг Земли?»;
Восполняющий: «Кто
изобрел автомобиль?».
Слайд 53
Вопросы необходимо ставить корректно.
Вопрос нужно формулировать кратко и
ясно.
Полезно избегать риторических вопросов.
Из вопроса должны быть ясны время,
место и тот контекст, который необходимо учитывать при ответе.В вопросе не следует употреблять многозначные слова.
При необходимости конкретизации ответа в вопрос можно ввести краткое предисловие.
Формулировка вопроса и его смысл должны, как правило, учитывать личный персональный опыт опрашиваемых в той области, которой касается вопрос.
Правила постановки вопрсов
Слайд 55
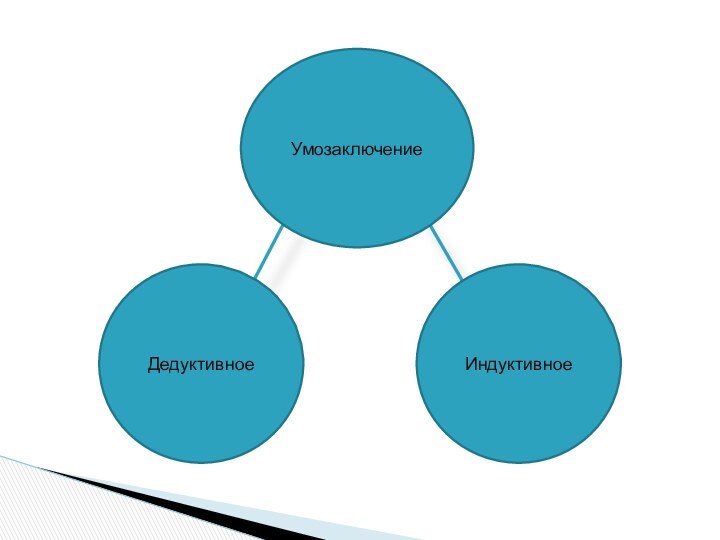
7. Умозаключения
Умозаключение – логическая операция, в результате которой
из одного или нескольких принятых утверждений (посылок) получается новое
утверждение – заключение (вывод, следствие).
Слайд 57
В основе дедуктивного умозаключения лежит
логический закон, в силу
чего заключение с
логической необходимостью вытекает из
принятых посылок.
Например:
Если идет дождь,
земля является мокрой.Идет дождь.
Земля мокрая.
Слайд 58
В индуктивном умозаключении связь посылок
и заключения опирается не
на закон логики,
а на некоторые фактические или
психологические основания, не
имеющиечисто формального характера.
Например,
Аргентина является республикой; Бразилия – республика;
Венесуэла – республика; Эквадор – республика.
Аргентина, Бразилия, Венесуэла, Эквадор – латиноамериканские государства.
Значит, все латиноамериканские государства являются республиками.
Слайд 59 Таким образом, с точки зрения логической
грамматики, механизм человеческого мышления является простым. Имеются многообразные имена,
в частности, понятия, обозначающие отдельные предметы и их множества. С помощью логических связок из понятий складываются высказывания. Из высказываний состоят рассуждения. Те рассуждения, в которых какие-то высказывания принимаются за исходное, а из них выводится новое высказывание, называются умозаключениями.Заключение
Слайд 60
Глоссарий
Логика – наука о законах и операциях правильного
мышления.
Имя – это выражение языка, обозначающее отдельный предмет или
совокупность сходных предметов.Понятие – общее имя с относительно ясным и устойчивым содержанием, используемое в обычном языке или в языке науки.
Равнозначность - отношение между понятиями, объемы
которых полностью совпадают.
Слайд 61
Глоссарий
Пересечение - отношение между понятиями, объемы которых частично
совпадают.
Подчинение – отношение между понятиями, объем одного из
которых полностью входит в объем другого. Исключение – отношение между понятиями, объемы которых полностью исключают друг друга.
Суждение - представляет собой мысль, выражаемую высказыванием.
Слайд 62
Глоссарий
Вопрос - это выраженное в форме вопросительного предложение
пожелание, направленное на развитие, уточнение или дополнение имеющегося знания.
Дедукция - введение заключений, столь же достоверных, как и принятые посылки.
Умозаключение – логическая операция, в результате которой из одного или нескольких принятых утверждений (посылок) получается новое утверждение – заключение (вывод, следствие).
Индукция – выведение вероятных (правдоподобных) заключений.





























