Слайд 2
Пересечение многогранной и кривой поверхностей
Последовательность решения задач на
построение линии пересечения поверхностей:
1) выясняем вид и расположение заданных
поверхностей относительно друг друга (врезка или проницание) и плоскостей проекций (задана ли проецирующая поверхность – цилиндр или призма);
2) определяем характер линии пересечения - совокупность плоских кривых;
3) определяем опорные точки (на ребрах многогранников, экстремальные и очерковые);
4) определяем промежуточные точки;
5) соединяем найденные точки. Определяем видимость проекций линии пересечения и очерков поверхностей, обводим чертеж.
Слайд 3
Пересечение многогранной и кривой поверхностей
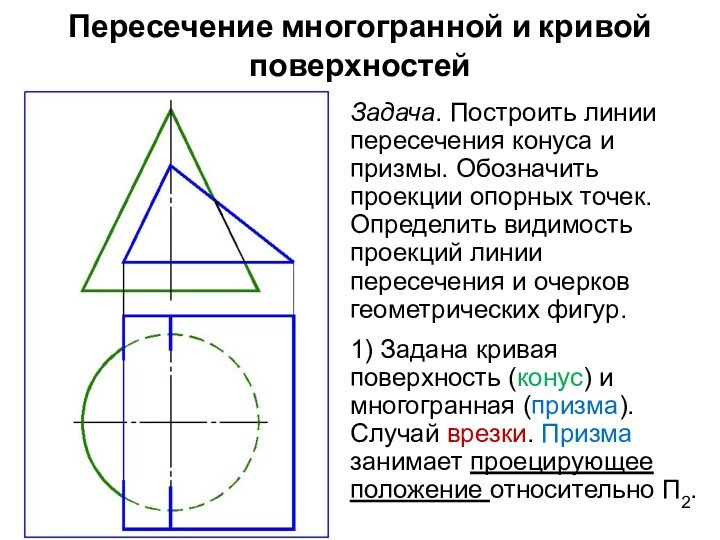
Задача. Построить линии пересечения
конуса и призмы. Обозначить проекции опорных точек. Определить видимость
проекций линии пересечения и очерков геометрических фигур.
1) Задана кривая поверхность (конус) и многогранная (призма). Случай врезки. Призма занимает проецирующее положение относительно П2.
Слайд 4
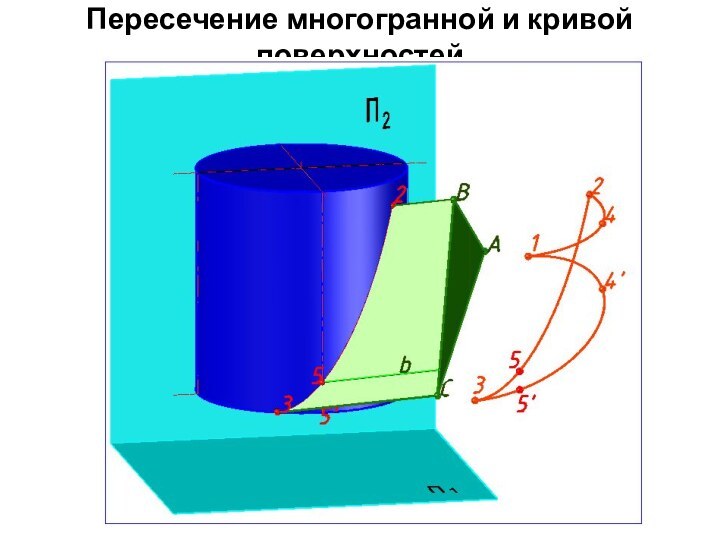
Пересечение многогранной и кривой поверхностей
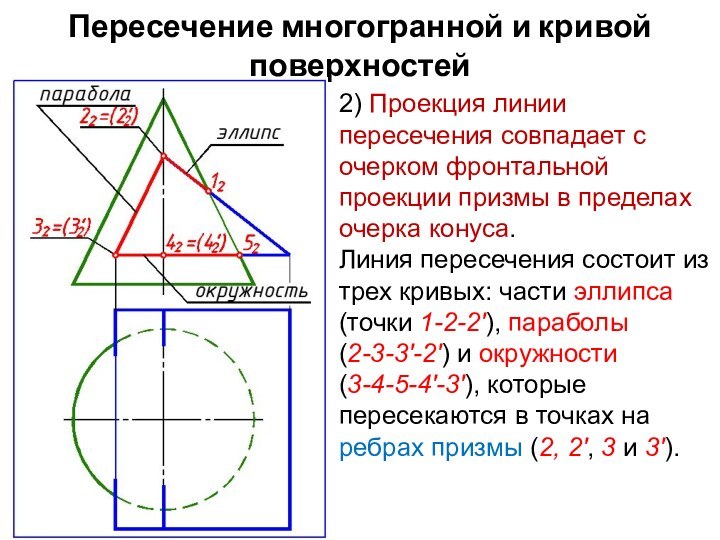
2) Проекция линии пересечения
совпадает с очерком фронтальной проекции призмы в пределах очерка
конуса.
Линия пересечения состоит из трех кривых: части эллипса
(точки 1-2-2'), параболы
(2-3-3'-2') и окружности
(3-4-5-4'-3'), которые пересекаются в точках на ребрах призмы (2, 2', 3 и 3').
Слайд 5
Пересечение многогранной и кривой поверхностей
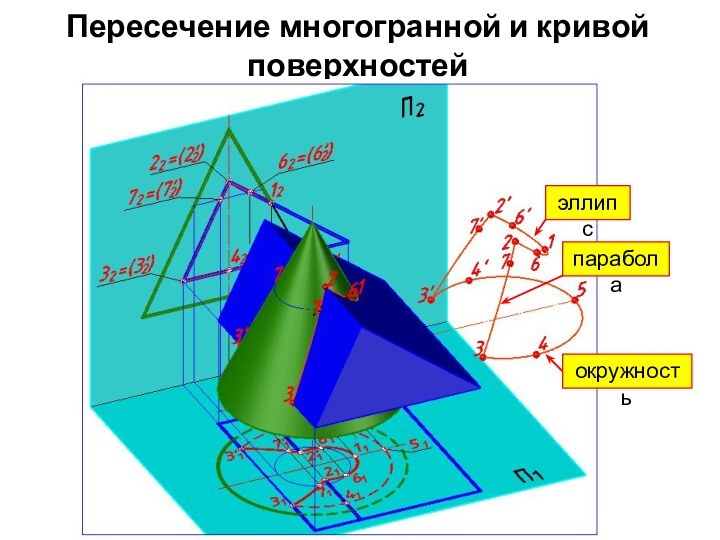
эллипс
окружность
парабола
Слайд 6
Пересечение многогранной и кривой поверхностей
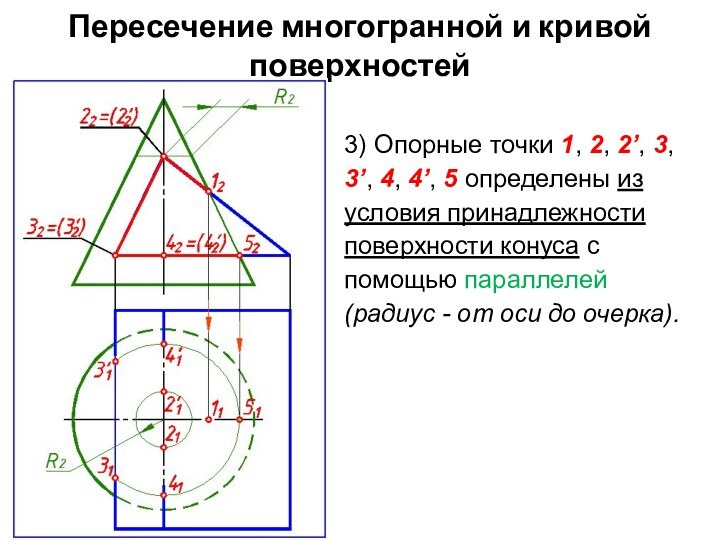
3) Опорные точки 1,
2, 2’, 3, 3’, 4, 4’, 5 определены из
условия принадлежности поверхности конуса с помощью параллелей (радиус - от оси до очерка).
Слайд 7
Пересечение многогранной и кривой поверхностей
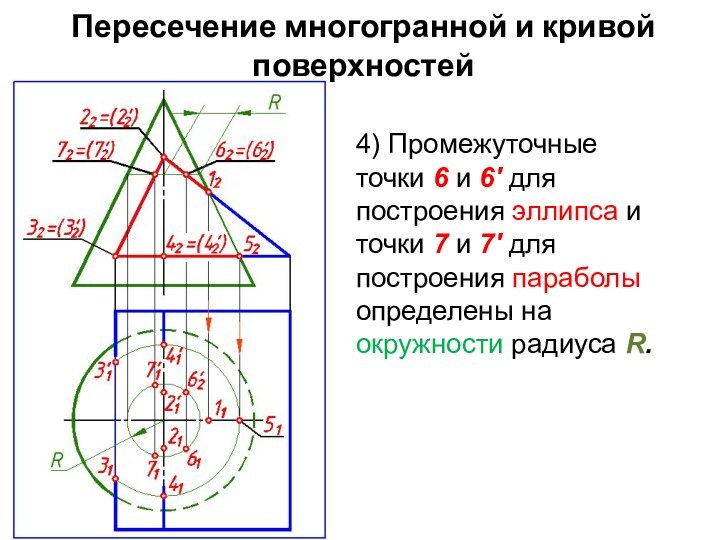
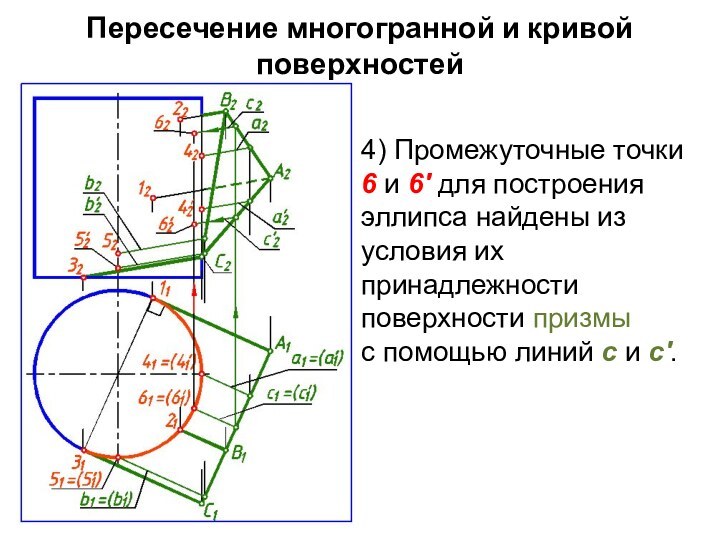
4) Промежуточные точки 6
и 6' для построения эллипса и точки 7 и
7' для построения параболы определены на окружности радиуса R.
Слайд 8
Пересечение многогранной и кривой поверхностей
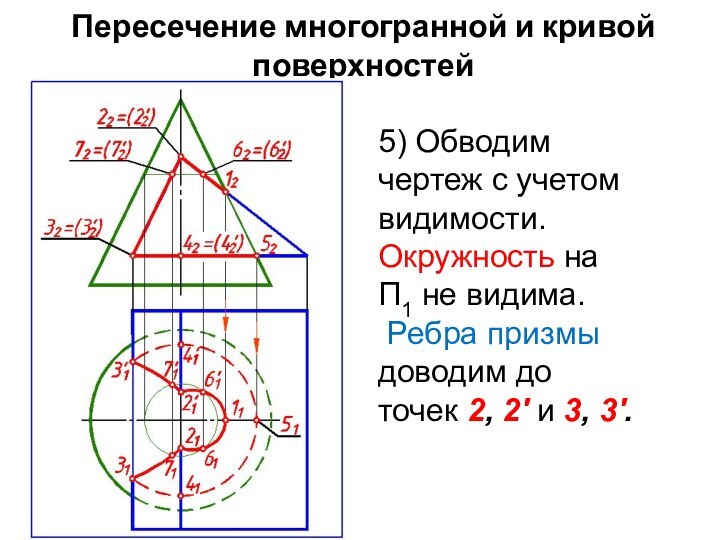
5) Обводим чертеж с
учетом видимости. Окружность на П1 не видима.
Ребра призмы
доводим до точек 2, 2' и 3, 3'.
Слайд 9
Пересечение многогранной и кривой поверхностей
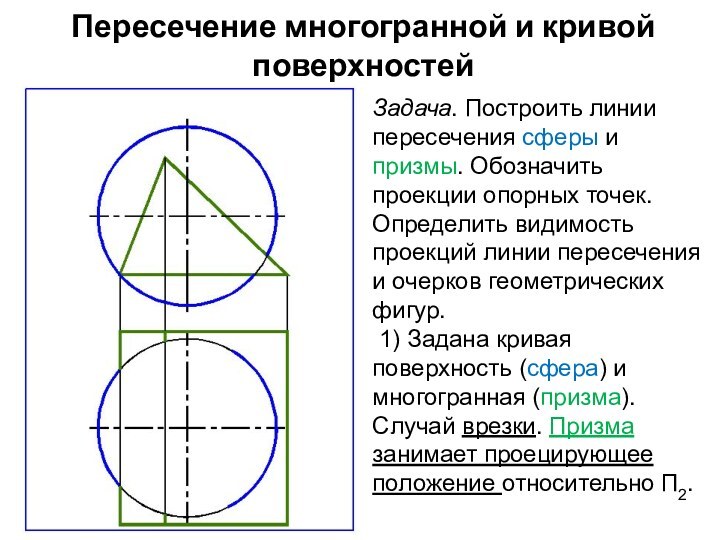
Задача. Построить линии пересечения
сферы и призмы. Обозначить проекции опорных точек. Определить видимость
проекций линии пересечения и очерков геометрических фигур.
1) Задана кривая поверхность (сфера) и многогранная (призма). Случай врезки. Призма занимает проецирующее положение относительно П2.
Слайд 10
Пересечение многогранной и кривой поверхностей
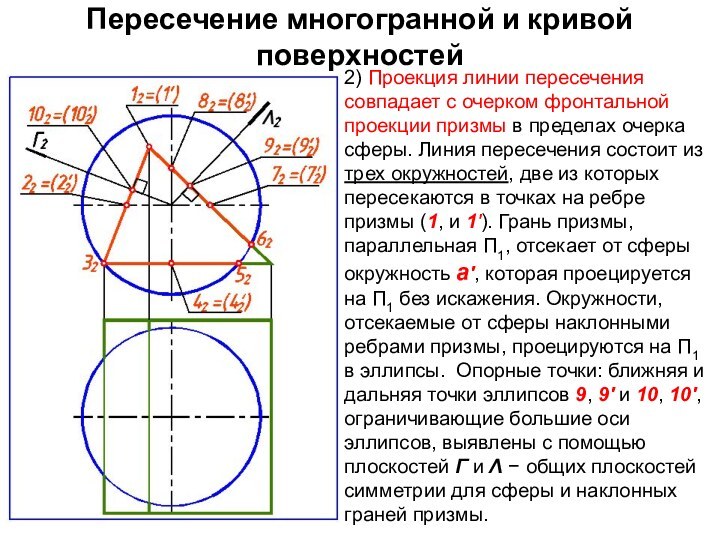
2) Проекция линии пересечения
совпадает с очерком фронтальной проекции призмы в пределах очерка
сферы. Линия пересечения состоит из трех окружностей, две из которых пересекаются в точках на ребре призмы (1, и 1'). Грань призмы, параллельная П1, отсекает от сферы окружность а', которая проецируется на П1 без искажения. Окружности, отсекаемые от сферы наклонными ребрами призмы, проецируются на П1 в эллипсы. Опорные точки: ближняя и дальняя точки эллипсов 9, 9' и 10, 10', ограничивающие большие оси эллипсов, выявлены с помощью плоскостей Г и Λ общих плоскостей симметрии для сферы и наклонных граней призмы.
Слайд 11
Пересечение многогранной и кривой поверхностей
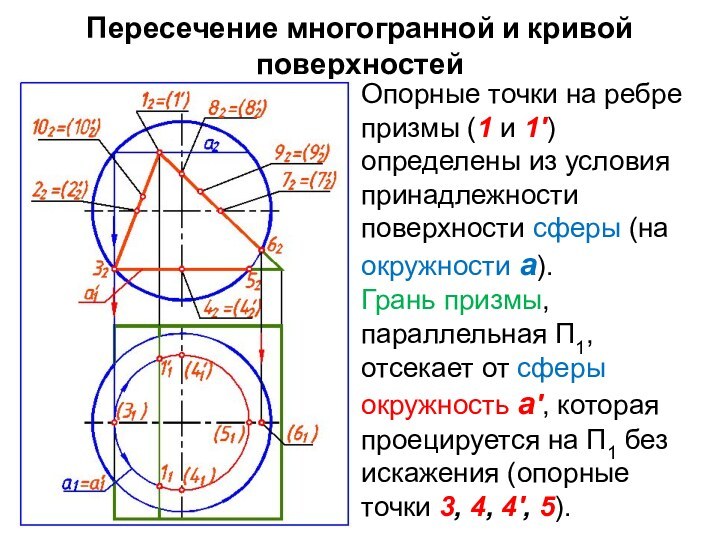
Опорные точки на ребре
призмы (1 и 1') определены из условия принадлежности поверхности
сферы (на окружности а).
Грань призмы, параллельная П1, отсекает от сферы окружность а', которая проецируется на П1 без искажения (опорные точки 3, 4, 4', 5).
Слайд 12
Пересечение многогранной и кривой поверхностей
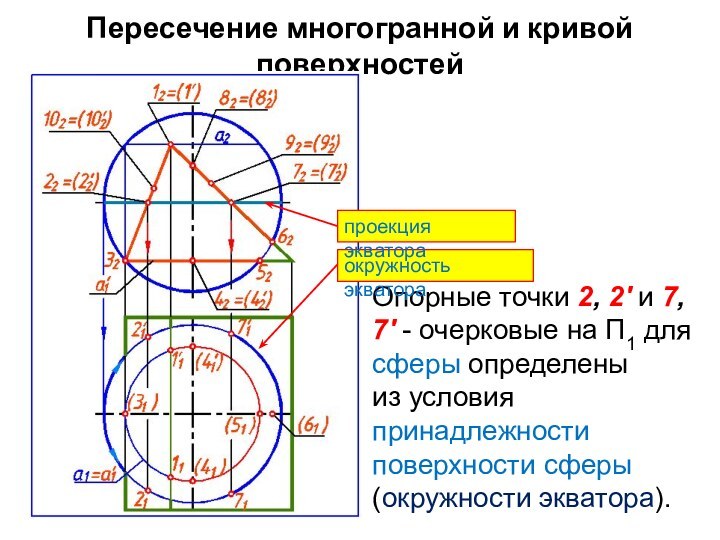
Опорные точки 2, 2'
и 7, 7' - очерковые на П1 для сферы
определены
из условия принадлежности поверхности сферы (окружности экватора).
окружность экватора
проекция экватора
Слайд 13
Пересечение многогранной и кривой поверхностей
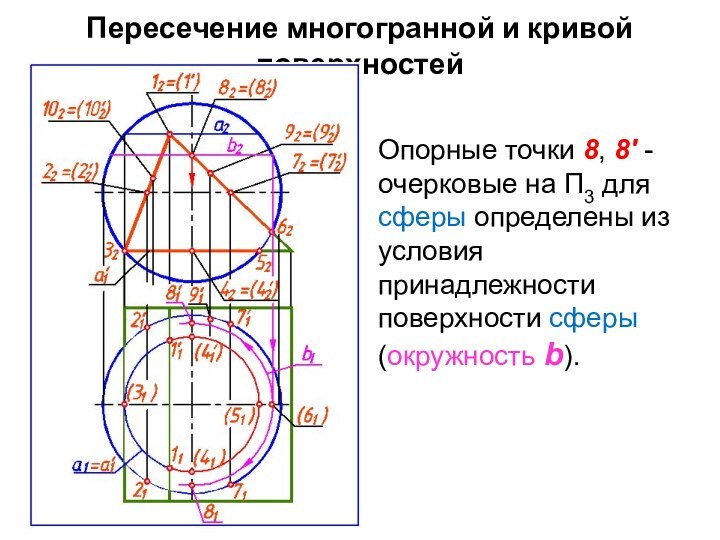
Опорные точки 8, 8'
- очерковые на П3 для сферы определены из условия
принадлежности поверхности сферы (окружность b).
Слайд 14
Пересечение многогранной и кривой поверхностей
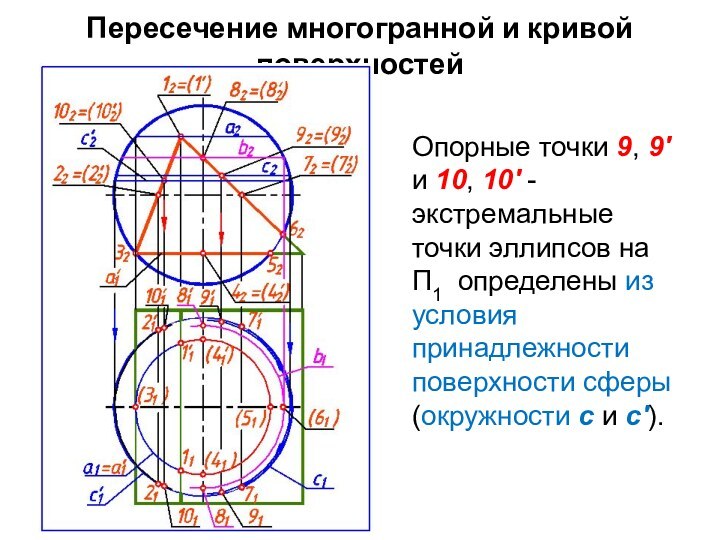
Опорные точки 9, 9'
и 10, 10′ - экстремальные точки эллипсов на П1
определены из условия принадлежности поверхности сферы (окружности c и c').
Слайд 15
Пересечение многогранной и кривой поверхностей
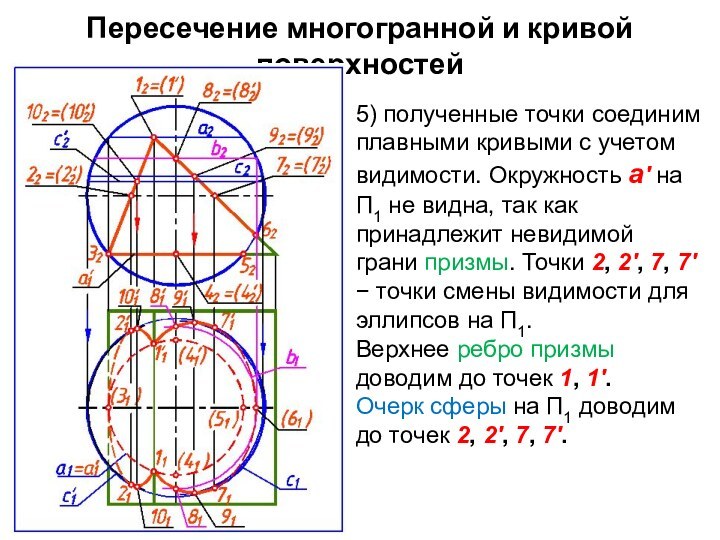
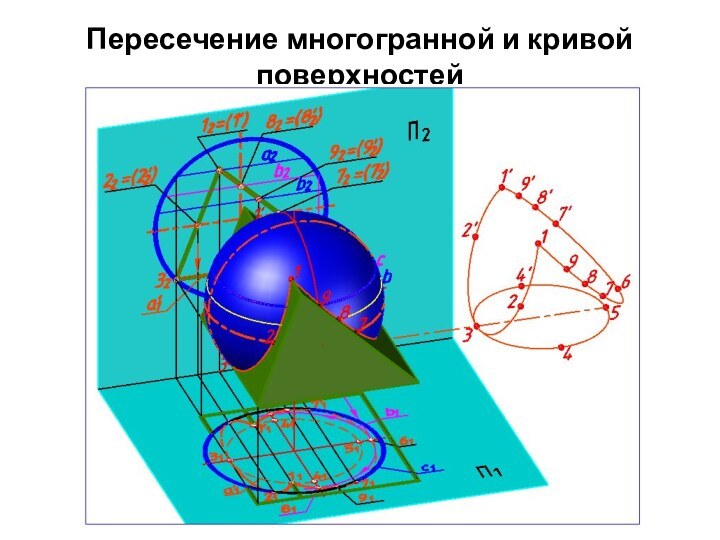
5) полученные точки соединим
плавными кривыми с учетом видимости. Окружность а' на П1
не видна, так как принадлежит невидимой грани призмы. Точки 2, 2', 7, 7' точки смены видимости для эллипсов на П1.
Верхнее ребро призмы доводим до точек 1, 1'.
Очерк сферы на П1 доводим до точек 2, 2', 7, 7'.
Слайд 16
Пересечение многогранной и кривой поверхностей
Слайд 17
Пересечение многогранной и кривой поверхностей
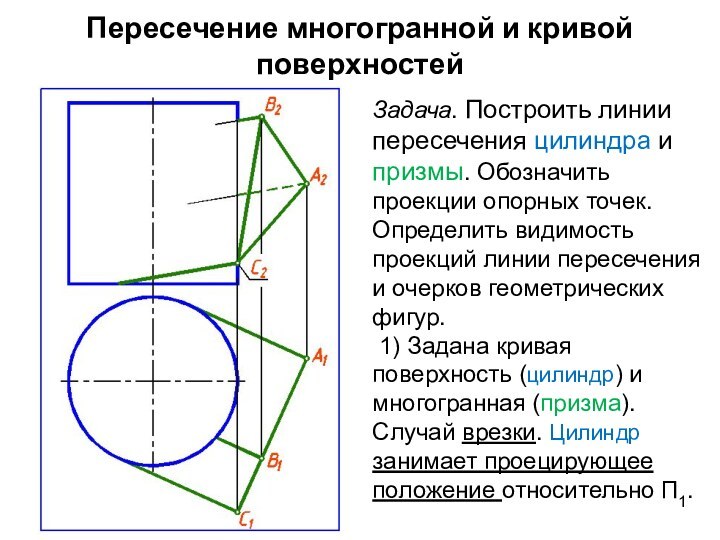
Задача. Построить линии пересечения
цилиндра и призмы. Обозначить проекции опорных точек. Определить видимость
проекций линии пересечения и очерков геометрических фигур.
1) Задана кривая поверхность (цилиндр) и многогранная (призма). Случай врезки. Цилиндр занимает проецирующее положение относительно П1.
Слайд 18
Пересечение многогранной и кривой поверхностей
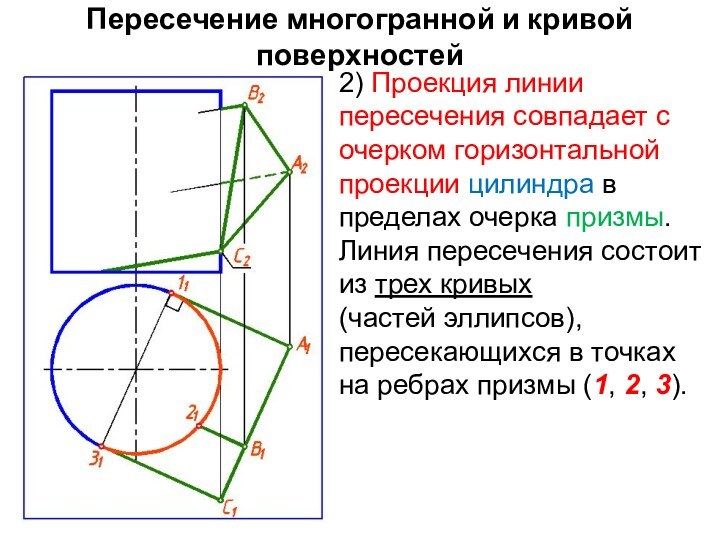
2) Проекция линии пересечения
совпадает с очерком горизонтальной проекции цилиндра в пределах очерка
призмы. Линия пересечения состоит из трех кривых
(частей эллипсов), пересекающихся в точках на ребрах призмы (1, 2, 3).
Слайд 19
Пересечение многогранной и кривой поверхностей
Слайд 20
Пересечение многогранной и кривой поверхностей
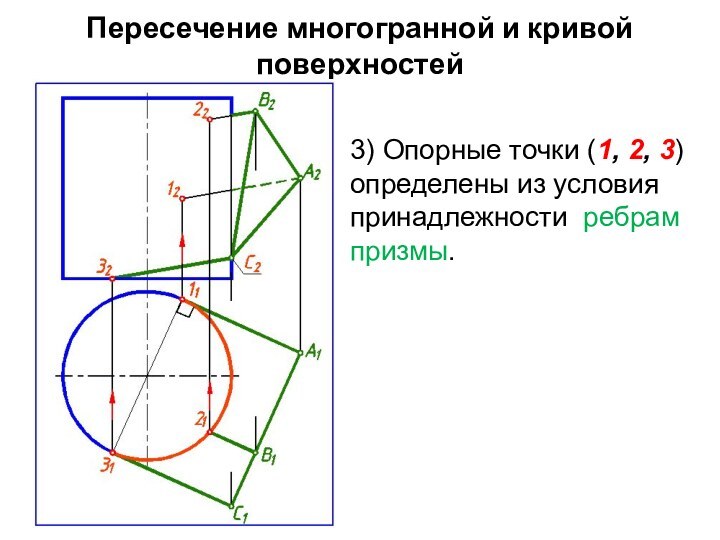
3) Опорные точки (1,
2, 3) определены из условия принадлежности ребрам призмы.
Слайд 21
Пересечение многогранной и кривой поверхностей
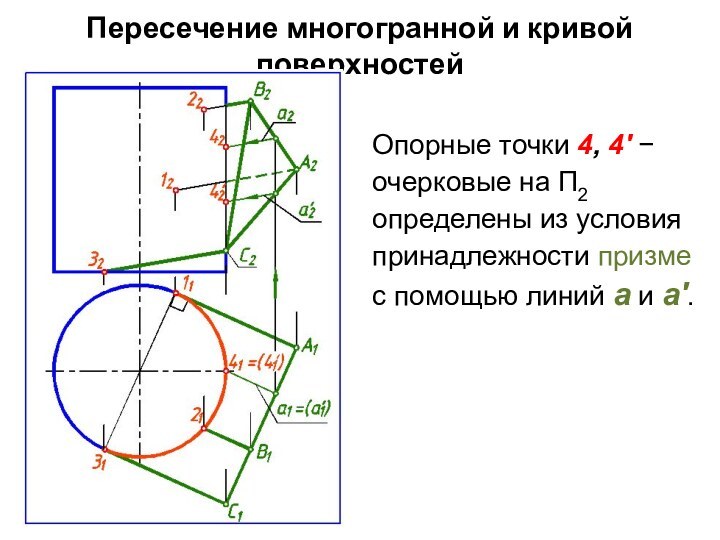
Опорные точки 4, 4′
очерковые на П2 определены из условия принадлежности призме
с помощью линий а и а'.
Слайд 22
Пересечение многогранной и кривой поверхностей
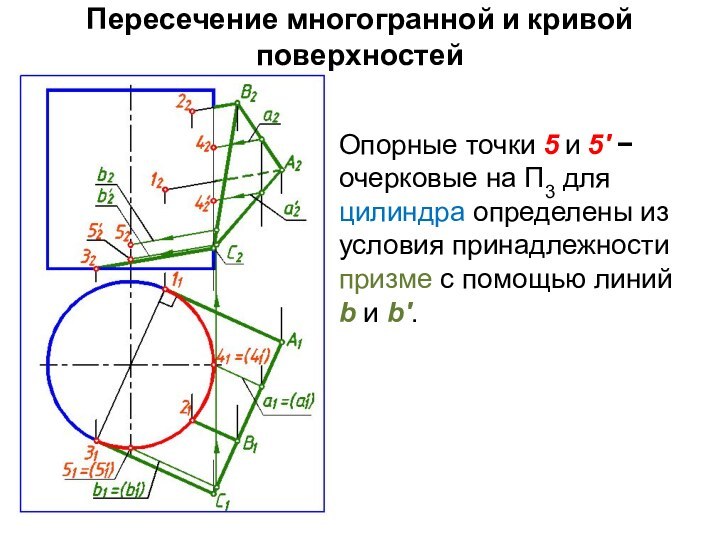
Опорные точки 5 и
5' очерковые на П3 для цилиндра определены из
условия принадлежности призме с помощью линий
b и b'.
Слайд 23
Пересечение многогранной и кривой поверхностей
4) Промежуточные точки 6
и 6' для построения эллипса найдены из условия их
принадлежности поверхности призмы
с помощью линий с и с'.
Слайд 24
Пересечение многогранной и кривой поверхностей
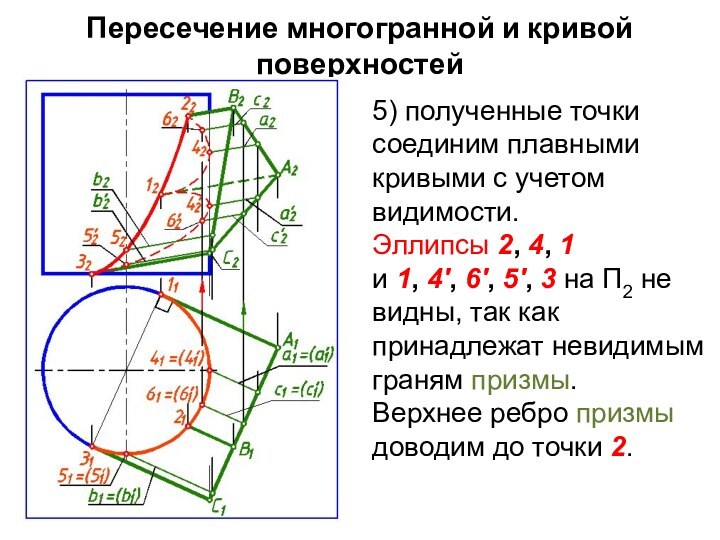
5) полученные точки соединим
плавными кривыми с учетом видимости.
Эллипсы 2, 4, 1
и 1,
4', 6', 5', 3 на П2 не видны, так как принадлежат невидимым граням призмы.
Верхнее ребро призмы доводим до точки 2.
Слайд 25
Пересечение многогранной и кривой поверхностей
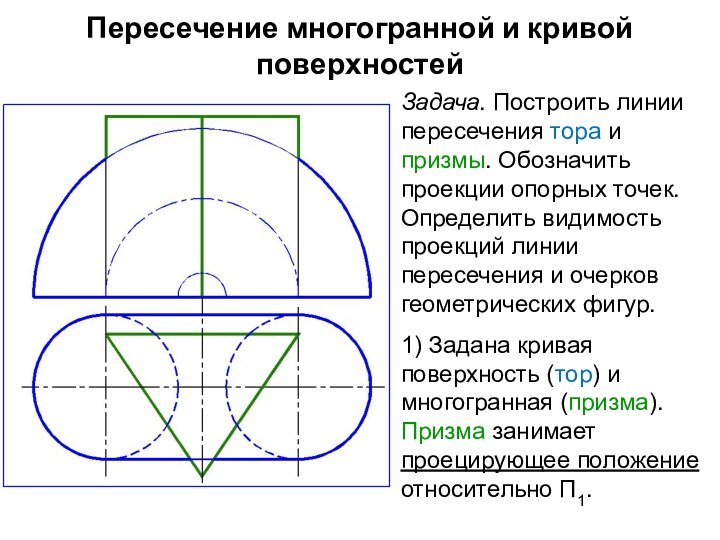
Задача. Построить линии пересечения
тора и призмы. Обозначить проекции опорных точек. Определить видимость
проекций линии пересечения и очерков геометрических фигур.
1) Задана кривая поверхность (тор) и многогранная (призма). Призма занимает проецирующее положение относительно П1.
Слайд 26
Пересечение многогранной и кривой поверхностей
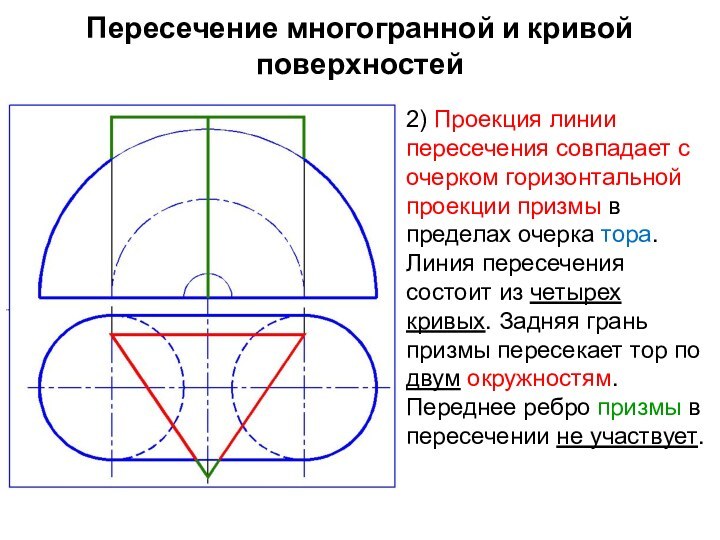
2) Проекция линии пересечения
совпадает с очерком горизонтальной проекции призмы в пределах очерка
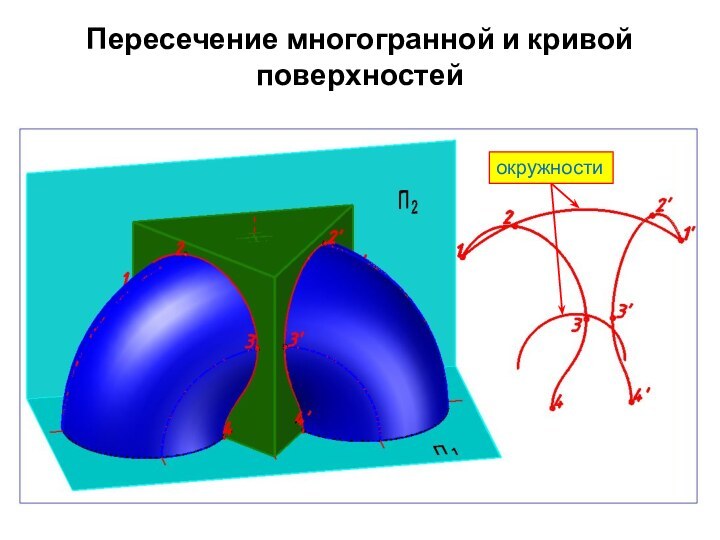
тора. Линия пересечения состоит из четырех кривых. Задняя грань призмы пересекает тор по двум окружностям. Переднее ребро призмы в пересечении не участвует.
Слайд 27
Пересечение многогранной и кривой поверхностей
окружности
Слайд 28
Пересечение многогранной и кривой поверхностей
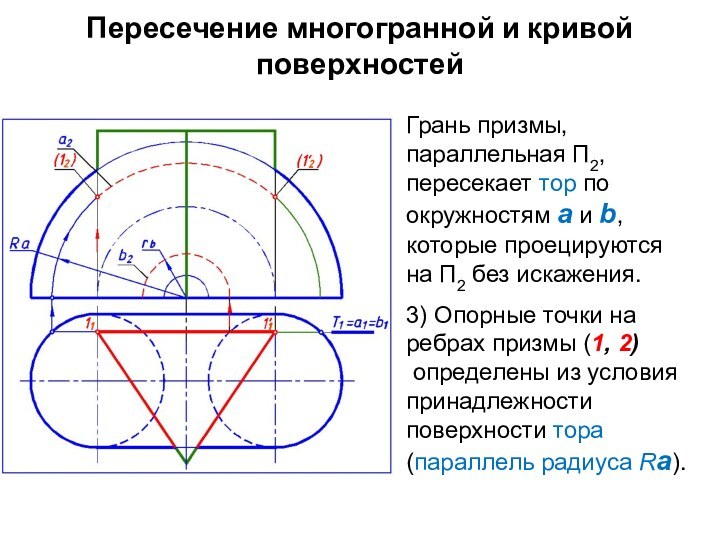
Грань призмы, параллельная П2,
пересекает тор по окружностям а и b, которые проецируются
на
П2 без искажения.
3) Опорные точки на ребрах призмы (1, 2)
определены из условия принадлежности
поверхности тора (параллель радиуса Rа).
Слайд 29
Пересечение многогранной и кривой поверхностей
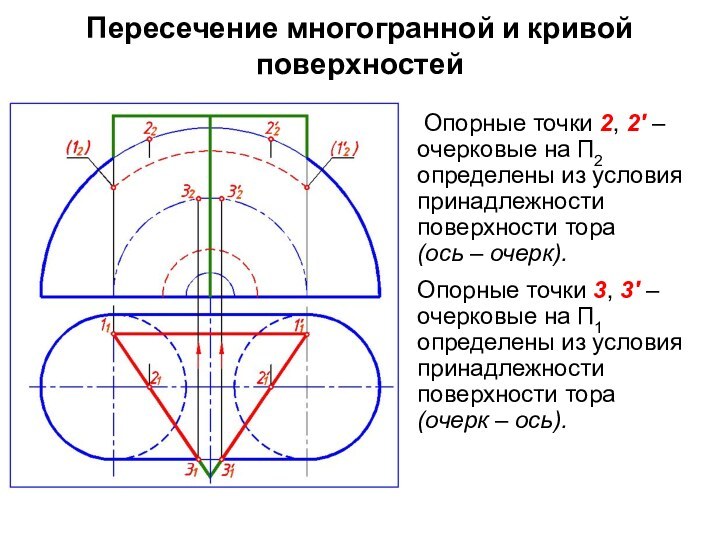
Опорные точки 2,
2′ –очерковые на П2
определены из условия принадлежности поверхности
тора
(ось – очерк).
Опорные точки 3, 3′ –очерковые на П1
определены из условия принадлежности поверхности тора
(очерк – ось).
Слайд 30
Пересечение многогранной и кривой поверхностей
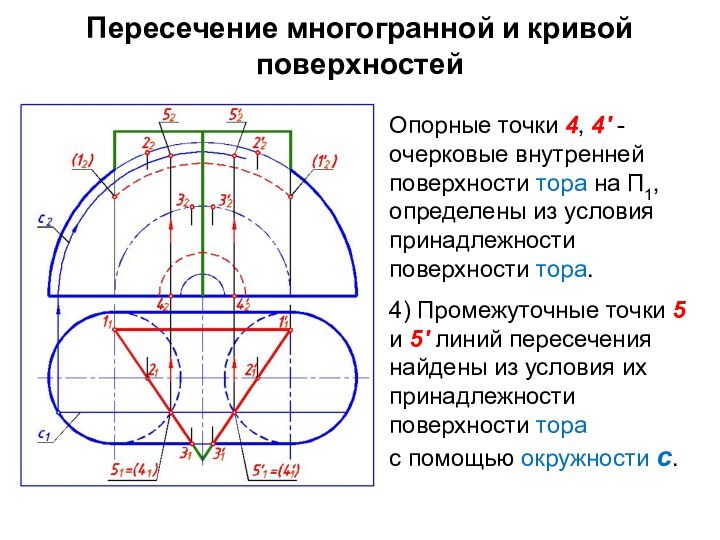
Опорные точки 4, 4′
-очерковые внутренней поверхности тора на П1,
определены из условия
принадлежности поверхности тора.
4) Промежуточные точки 5 и 5' линий пересечения найдены из условия их принадлежности поверхности тора
с помощью окружности с.
Слайд 31
Пересечение многогранной и кривой поверхностей
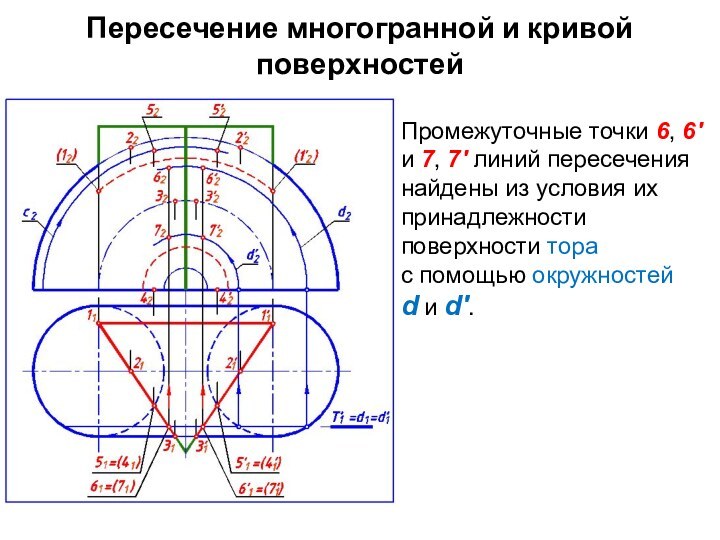
Промежуточные точки 6, 6'
и 7, 7' линий пересечения найдены из условия их
принадлежности поверхности тора
с помощью окружностей
d и d'.
Слайд 32
Пересечение многогранной и кривой поверхностей
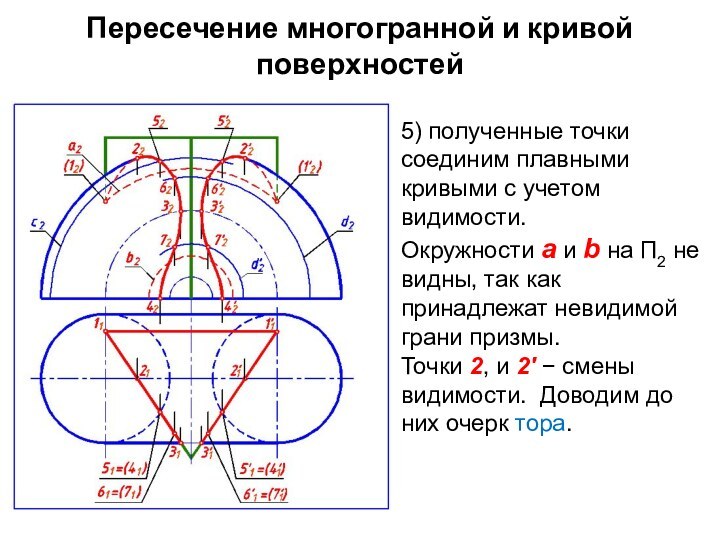
5) полученные точки соединим
плавными кривыми с учетом видимости.
Окружности а и b на
П2 не видны, так как принадлежат невидимой грани призмы.
Точки 2, и 2′ смены видимости. Доводим до них очерк тора.
Слайд 33
Пересечение многогранной и кривой поверхностей
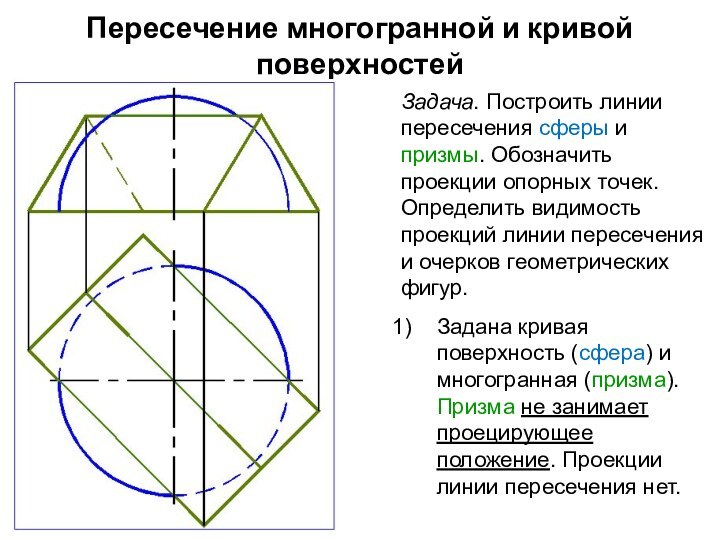
Задача. Построить линии пересечения
сферы и призмы. Обозначить проекции опорных точек. Определить видимость
проекций линии пересечения и очерков геометрических фигур.
Задана кривая поверхность (сфера) и многогранная (призма). Призма не занимает проецирующее положение. Проекции линии пересечения нет.
Слайд 34
Пересечение многогранной и кривой поверхностей
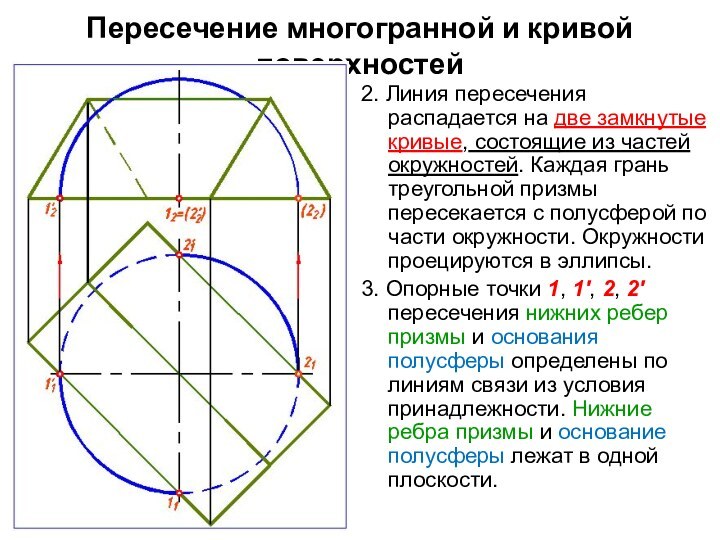
2. Линия пересечения распадается
на две замкнутые кривые, состоящие из частей окружностей. Каждая
грань треугольной призмы пересекается с полусферой по части окружности. Окружности проецируются в эллипсы.
3. Опорные точки 1, 1', 2, 2' пересечения нижних ребер призмы и основания полусферы определены по линиям связи из условия принадлежности. Нижние ребра призмы и основание полусферы лежат в одной плоскости.
Слайд 35
Пересечение многогранной и кривой поверхностей
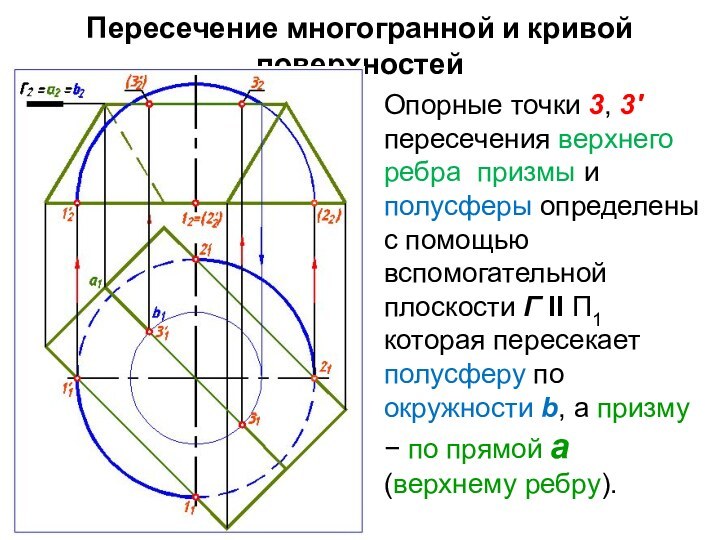
Опорные точки 3, 3'
пересечения верхнего ребра призмы и полусферы определены с помощью
вспомогательной плоскости Г II П1 которая пересекает полусферу по окружности b, а призму по прямой а (верхнему ребру).
Слайд 36
Пересечение многогранной и кривой поверхностей
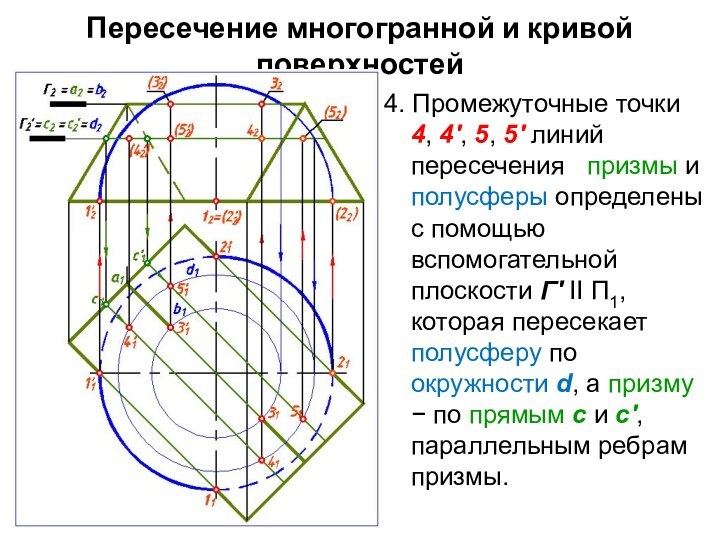
4. Промежуточные точки 4,
4', 5, 5' линий пересечения призмы и полусферы
определены с помощью вспомогательной плоскости Г' II П1, которая пересекает полусферу по окружности d, а призму по прямым с и с′, параллельным ребрам призмы.
Слайд 37
Пересечение многогранной и кривой поверхностей
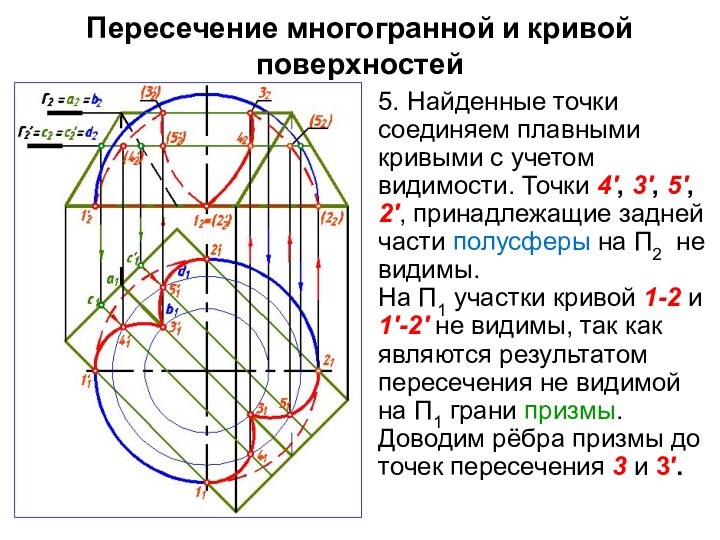
5. Найденные точки соединяем
плавными кривыми с учетом видимости. Точки 4', 3', 5',
2', принадлежащие задней части полусферы на П2 не видимы.
На П1 участки кривой 1-2 и 1'-2' не видимы, так как являются результатом пересечения не видимой на П1 грани призмы.
Доводим рёбра призмы до точек пересечения 3 и 3′.
Слайд 38
Пересечение многогранной и кривой поверхностей
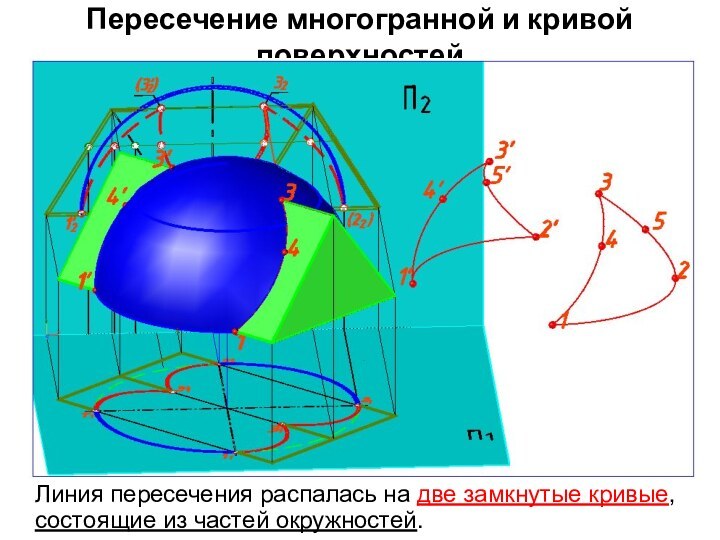
Линия пересечения распалась на
две замкнутые кривые, состоящие из частей окружностей.
Слайд 39
Пересечение многогранной и кривой поверхностей
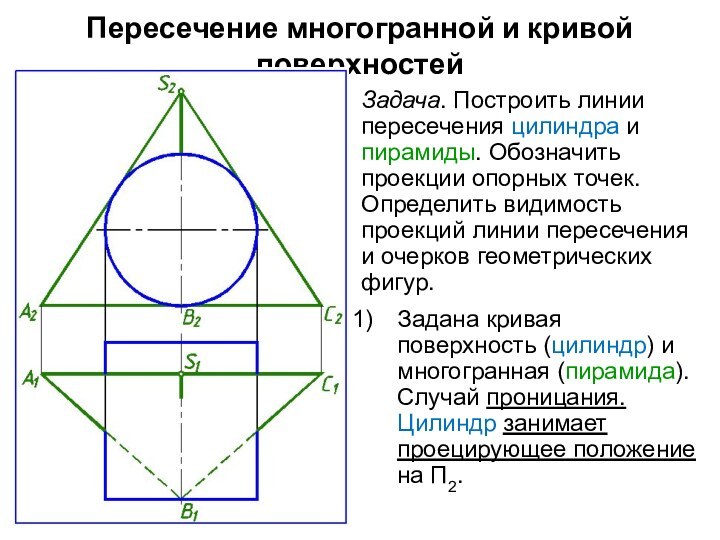
Задача. Построить линии пересечения
цилиндра и пирамиды. Обозначить проекции опорных точек. Определить видимость
проекций линии пересечения и очерков геометрических фигур.
Задана кривая поверхность (цилиндр) и многогранная (пирамида). Случай проницания. Цилиндр занимает проецирующее положение на П2.
Слайд 40
Пересечение многогранной и кривой поверхностей
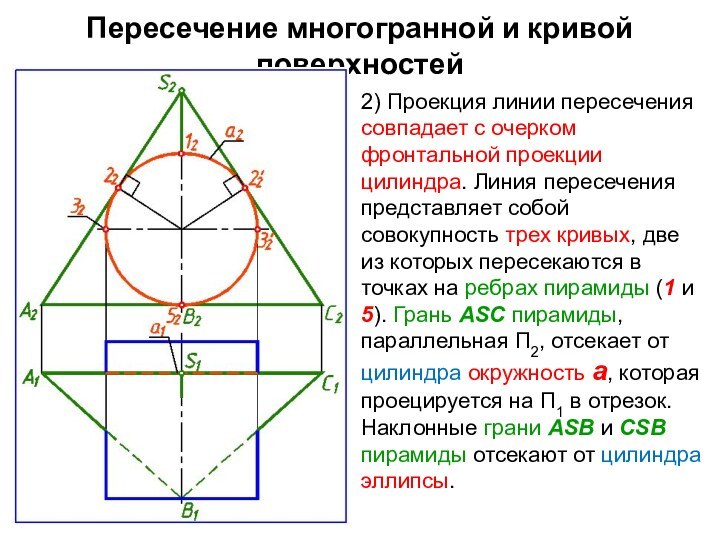
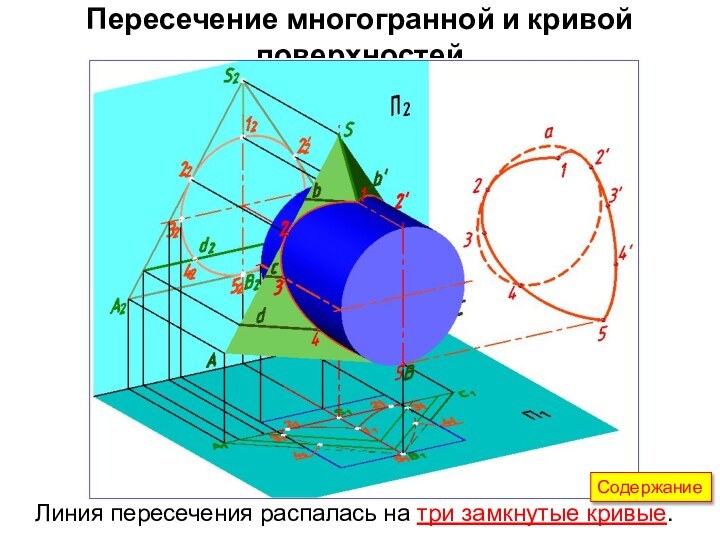
2) Проекция линии пересечения
совпадает с очерком фронтальной проекции цилиндра. Линия пересечения представляет
собой совокупность трех кривых, две из которых пересекаются в точках на ребрах пирамиды (1 и 5). Грань ASC пирамиды, параллельная П2, отсекает от цилиндра окружность а, которая проецируется на П1 в отрезок. Наклонные грани ASВ и СSВ пирамиды отсекают от цилиндра эллипсы.
Слайд 41
Пересечение многогранной и кривой поверхностей
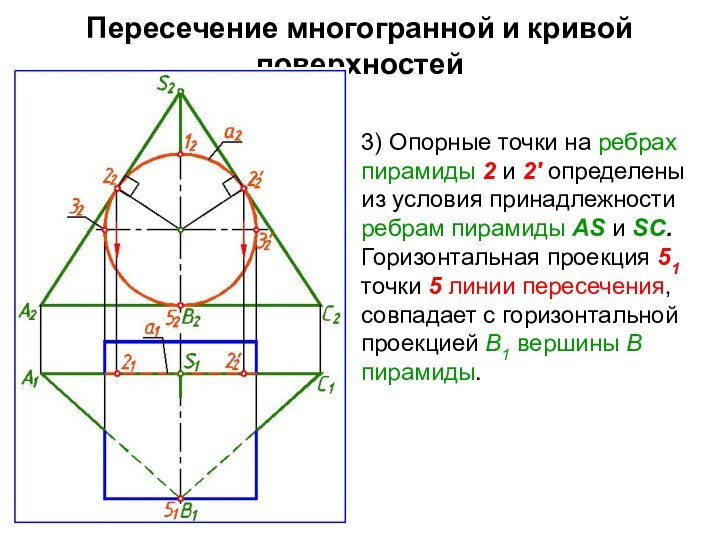
3) Опорные точки на
ребрах пирамиды 2 и 2' определены из условия принадлежности
ребрам пирамиды АS и SС.
Горизонтальная проекция 51 точки 5 линии пересечения, совпадает с горизонтальной проекцией В1 вершины В пирамиды.
Слайд 42
Пересечение многогранной и кривой поверхностей
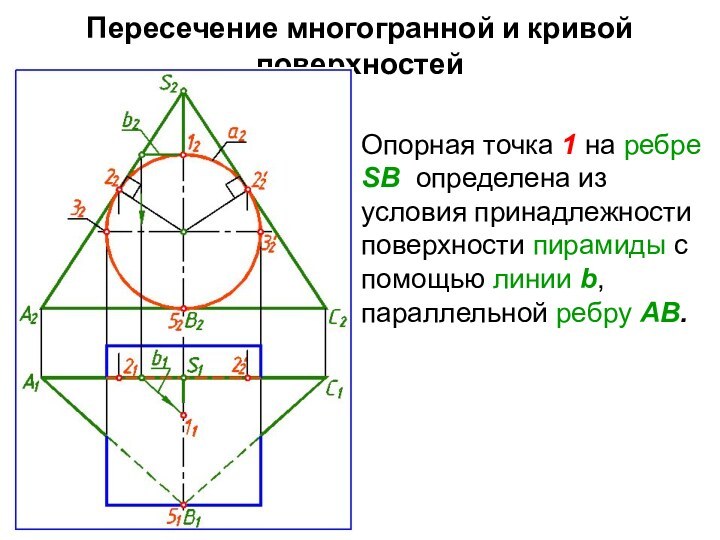
Опорная точка 1 на
ребре SВ определена из условия принадлежности поверхности пирамиды с
помощью линии b, параллельной ребру АВ.
Слайд 43
Пересечение многогранной и кривой поверхностей
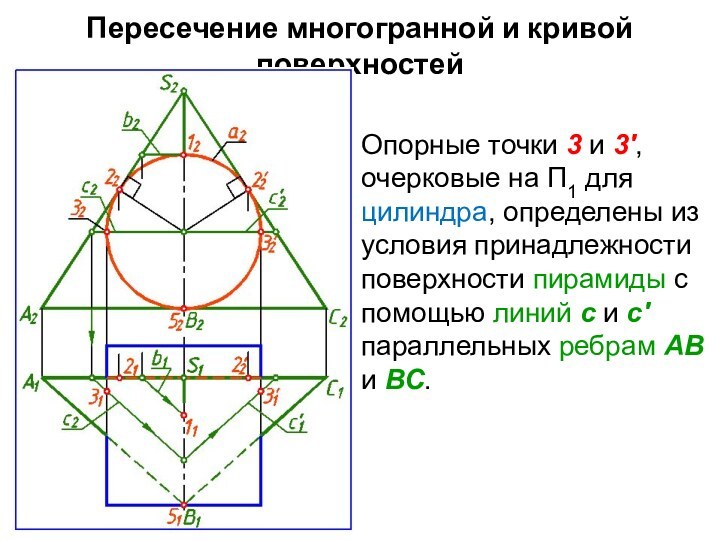
Опорные точки 3 и
3′, очерковые на П1 для цилиндра, определены из условия
принадлежности поверхности пирамиды с помощью линий с и с′ параллельных ребрам АВ и ВС.
Слайд 44
Пересечение многогранной и кривой поверхностей
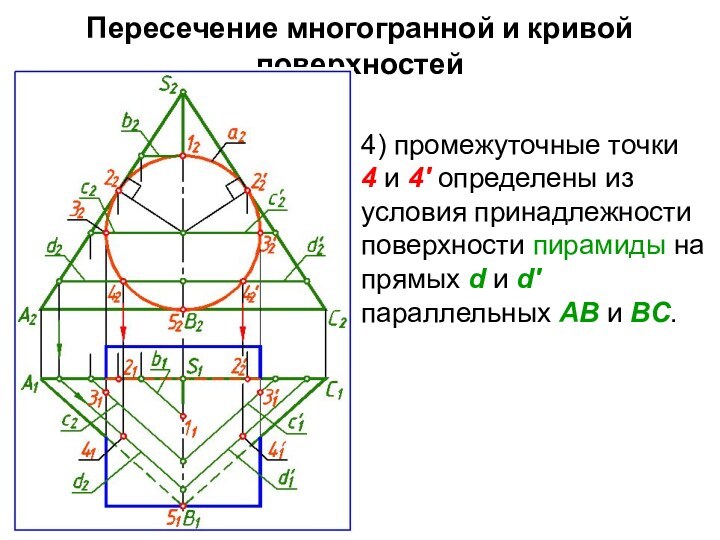
4) промежуточные точки
4 и
4' определены из условия принадлежности поверхности пирамиды на прямых
d и d′
параллельных АВ и ВС.
Слайд 45
Пересечение многогранной и кривой поверхностей
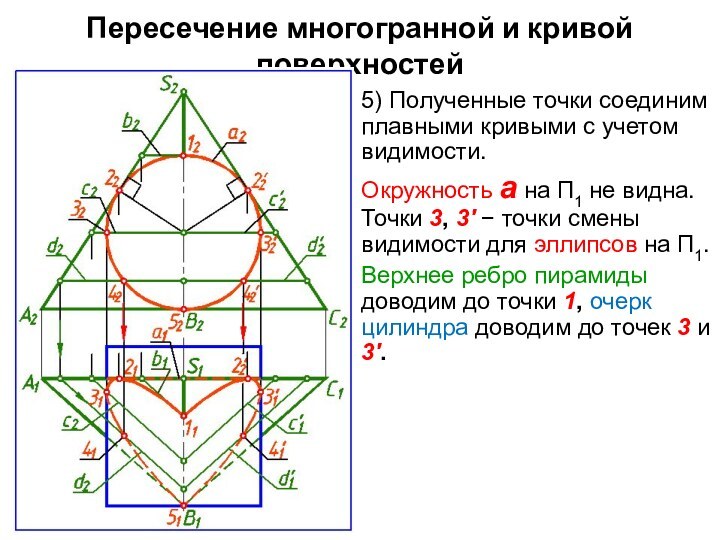
5) Полученные точки соединим
плавными кривыми с учетом видимости.
Окружность а на П1 не
видна.
Точки 3, 3' точки смены видимости для эллипсов на П1.
Верхнее ребро пирамиды доводим до точки 1, очерк цилиндра доводим до точек 3 и 3'.