Презентация на тему Преобразование пространства

плоскости какой-то другой точки этой же плоскости, причем любая

точка плоскости оказывается сопоставленной некоторой точке плоскости

Отображение плоскости на себя

–то точка этой плоскости, причем любая точка плоскости оказывается

сопоставленной некоторой точке. В таком случае говорят, что дано отображение плоскости на себя.

движение-
Под движением пространства понимается отображение пространства на себя,

при котором любые две точки и переходят (отображаются) в какие-то точки и так, что . Иными словами, движение пространства --- это отображение пространства на себя, сохраняющее расстояния между точками

Движение пространства

расстояние, называют – движением.

движении три точки, лежащие на прямой, переходят в три

точки, лежащие на другой прямой, причем точка, лежащая между двумя другими, переходит в точку, лежащую между образами двух других точек (сохраняется порядок их взаимного расположения).

Доказательство. Из планиметрии известно, что три точки A, B, C лежат на прямой тогда и только тогда, когда одна из них, например точка B, лежит между двумя другими - точками A и C, т.е. когда выполняется равенство

|AB| + |BC| = |AC|.

При движении расстояния сохраняются, а значит, соответствующее равенство выполняется и для точек A’, B’, C’:

|A’B’| + |B’C’| = |A’C’|.

Таким образом, точки A’, B’, C’ лежат на одной прямой и именно точка B’ лежит между A’ и C’.

Из данного свойства следуют также еще несколько свойств:

Свойства движения пространства

А

В

С

A’

С’

В’

Свойство 3. Образом прямой при движении

является прямая, а образом луча - луч.

Свойство 4. При движении образом треугольника является равный ему треугольник, образом плоскости - плоскость, причем параллельные плоскости отображаются на параллельные плоскости, образом полуплоскости - полуплоскость.

Свойство 5. При движении образом тетраэдра является тетраэдр, образом пространства - все пространство, образом полупространства - полупространство.

Свойство 6. При движении углы сохраняются, т.е. всякий угол отображается на угол того же вида и той же величины. Аналогичное верно и для двугранных углов.

все точки пространства перемещаются в одном и том же

направлении на одно и то же расстояние..
Параллельным переносом называется такое движение, при котором все точки плоскости перемещаются в одном и том же направлении на одинаковое расстояние

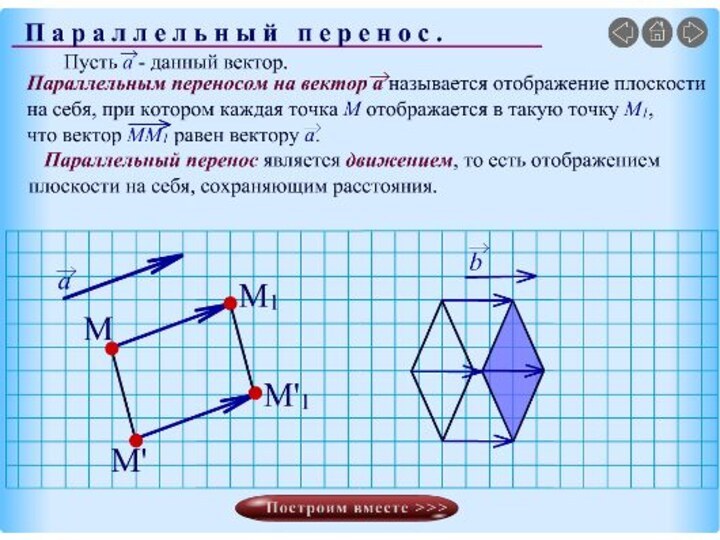
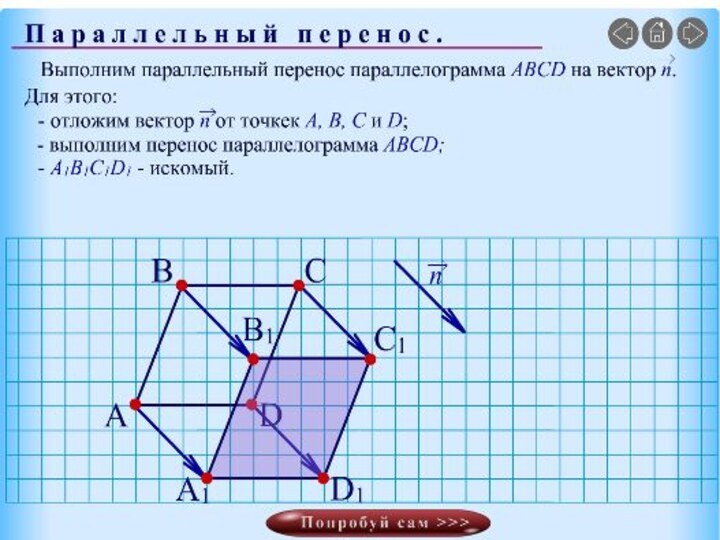
Параллельный перенос- (разные формулировки определения)

переносом, являются вершинами параллелограмма, в котором отрезок, соединяющий две

начальные точки образует одну сторону, а отрезок, соединяющий два их образа — противоположную ей сторону.
У параллельного переноса нет неподвижных точек, но имеются инвариантные прямые.
Совокупность всех параллельных переносов образует группу, которая в евклидовом пространстве является нормальной подгруппой группы движений, а в аффинном ― нормальной подгруппой группы аффинных преобразований

Свойства

развитие понятия параллельного переноса. Понятие параллельного переноса началось с

обычного параллелизма на евклидовой плоскости, для которой Фердинанд Миндинг в 1837 г. указал возможность обобщить её на случай поверхности в R 3 с помощью введенного им понятия развертывания кривой γ ∈ S на плоскость R 2 . Это указание Миндинга послужило отправным пунктом для Туллио Леви-Чивиты , который, оформляя аналитически параллельный перенос касательного вектора на поверхности, обнаружил зависимость его только от метрики поверхности и на этой основе обобщил его сразу на случай n-мерного риманова пространства. Дальнейшие обобщения этого понятия связаны с развитием общей теории связностей.

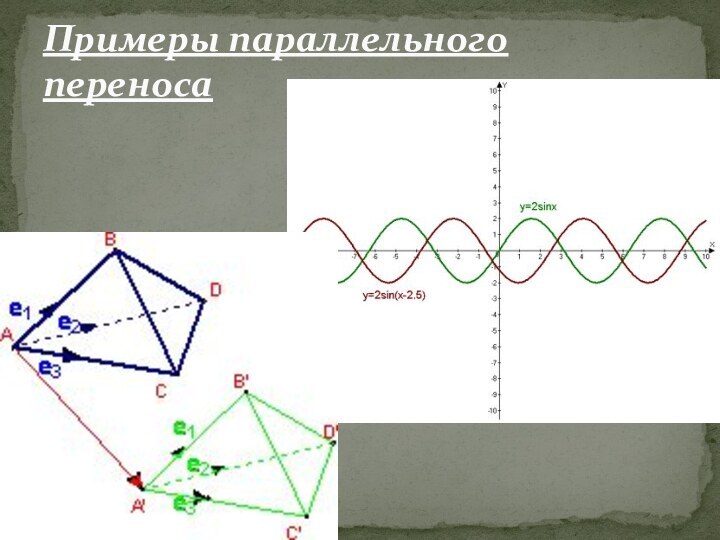
Дополнительная информация