- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Прямоугольная система координат в пространстве. Координаты вектора.
Содержание
- 2. Прямоугольная система координат
- 3. Если через точку пространства проведены три попарно
- 4. Прямые, с выбранными на них направлениями, называются
- 5. Вся система координат обозначается Охуz. Плоскости, проходящие
- 6. Точка О разделяет каждую из осей координат
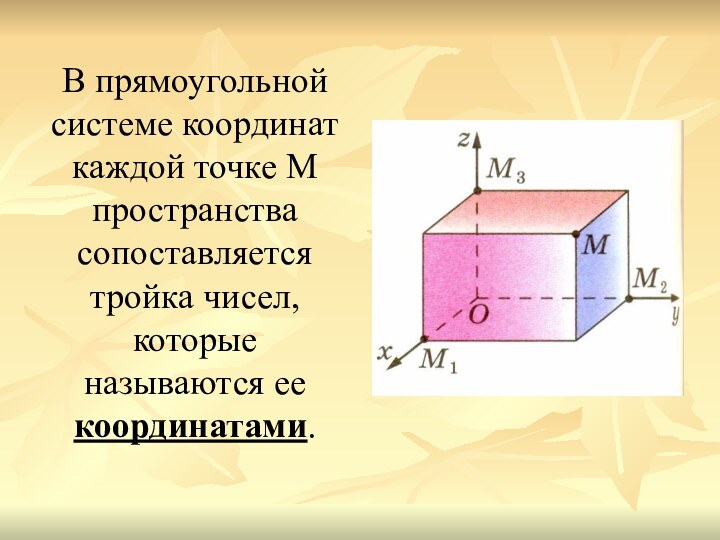
- 7. В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами.
- 8. На рисунке изображены шесть точек А (9;
- 9. Координаты вектора
- 10. Любой вектор можно разложить по
- 11. Коэффициенты х, у и z в разложении
- 12. Рассмотрим правила, которые позволяют по координатам данных
- 13. 10. Каждая координата суммы двух или более
- 14. 20. Каждая координата разности двух векторов равна
- 15. Скачать презентацию
- 16. Похожие презентации
Прямоугольная система координат














Слайд 4 Прямые, с выбранными на них направлениями, называются осями
координат, а их общая точка — началом координат. Она
обозначается обычно буквой О. Оси координат обозначаются так: Ох, Оу, Оz — и имеют названия: ось абсцисс, ось ординат, ось аппликат.Слайд 5 Вся система координат обозначается Охуz. Плоскости, проходящие соответственно
через оси координат Ох и Оу, Оу и Оz,
Оz и Ох, называются координатными плоскостями и обозначаются Оху, Оуz, Оzх.Слайд 6 Точка О разделяет каждую из осей координат на
два луча. Луч, направление которого совпадает с направлением оси,
называется положительной полуосью, а другой луч отрицательной полуосью.Слайд 7 В прямоугольной системе координат каждой точке М пространства
сопоставляется тройка чисел, которые называются ее координатами.
Слайд 8
На рисунке изображены шесть точек
А (9; 5;
10),
В (4; —3; 6),
С (9; 0; 0),
D (4; 0; 5),
Е (0; 3; 0),
F (0; 0; -3).





























