Слайд 2
Статистические гипотезы
Формулирование гипотез систематизирует предположения исследователя и представляет
их в лаконичном виде.
Различают два вида гипотез: научные и
статистические.
Научная гипотеза - это предполагаемое решение проблемы (формулируется как теорема).
Статистическая гипотеза – это предположение о распределении вероятностей, которое мы хотим проверить по имеющимся данным.
Слайд 3
Статистические гипотезы
Сmaтистические гипотезы подразделяются на:
нулевые,
альтернативные,
ненаправленные,
направленные.
Слайд 4
Статистические гипотезы
Нулевая гипотеза (обозначается как Но) - это
гипотеза об отсутствии значимых различий между какими-либо показателями или
о случайности связи между ними.
Гипотеза называется нулевой, потому что содержит 0 (Х1-Х2=0, Х1 и Х2 – сопоставляемые значения признаков).
Альтернативная гипотеза - это гипотеза о значимости различий между этими показателями или о достоверности связи между ними и обозначается как H1.
Альтернативная гипотеза – это то, что мы хотим доказать, поэтому её часто называют экспериментальной гипотезой.
Слайд 5
Статистические гипотезы
Например, необходимо выяснить, одинаков ли умственный уровень
у учеников школ № 1 и № 2. Перед
началом проведения исследования необходимо сформулировать соответствующие гипотезы. В нашем случае нулевая и альтернативная гипотезы будут выглядеть следующим образом.
Но : уровни умственного развития учеников школ № 1 и № 2 не отличаются друг от друга.
H1: уровни умственного уровня учеников школ № 1 и № 2 значимо различны.
Слайд 6
Направленная и ненаправленная гипотезы
Гипотеза называется ненаправленной, если ее
формулировка предполагает определение лишь отличий или не отличий Х1
и Х2 без указания направления этих отличий (в большую или меньшую сторону).
Если гипотеза содержит указание на направление отличий, например, Х1 не превышает Х2 (для гипотезы Но) или Х1 превышает Х2 (для гипотезы Н1) , то гипотеза рассматривается как направленная.
Примеры формулирования гипотез.
Направленные гипотезы Ненаправленные гипотезы
Но: x1 не превышает х2 Но: x1 не отличается от х2
Н1 : x1 превышает х2 Н1 : x1 отличается от х2
Слайд 7
Статистические критерии
Решение о наличии или отсутствии связей между
выборками по тем или иным измеряемым признакам принимается в
соответствии с определенным, так называемым, статистическим критерием.
Статистический критерий - это правило, обеспечивающее принятие выдвигаемой гипотезы как истинной и отклонение как ложной с высоким уровнем достоверности.
Слайд 8
Статистические критерии
Статистические критерии делятся на:
параметрические,
непараметрические,
односторонние,
двусторонние.
Слайд 9
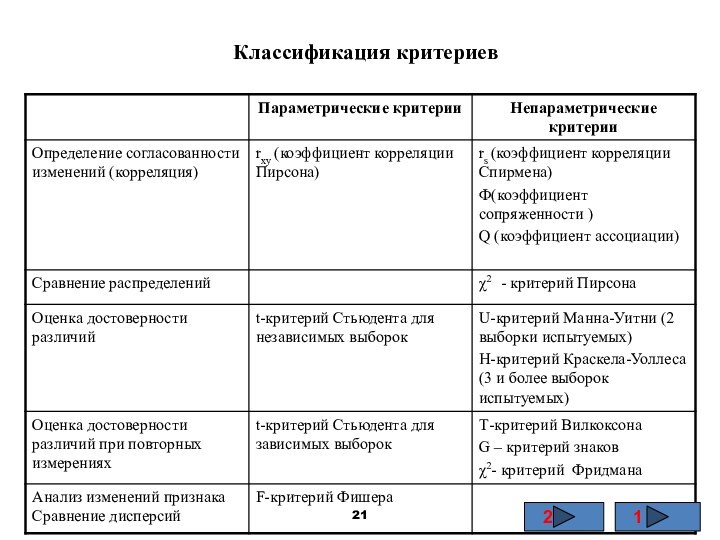
К параметрическим критериям относятся критерии, в вычислении которых
используются параметры распределения (средние значения и средне квадратичные отклонения).
К непараметрическим критериям относятся критерии, не требующие знание параметров распределения. Для их вычисления достаточно иметь значения частот или рангов.
Слайд 10
Параметрические критерии
Преимуществом параметрических критериев является то, что они
позволяют прямо оценить различия в средних или в дисперсиях
сравниваемых выборок.
Однако, их применение является корректным лишь по отношению к статистическим совокупностям, имеющим нормальные или близкие к нормальным распределения.
Кроме того, процедура их вычисления в сравнении с непараметрическими критериями несколько более сложная.
Слайд 11
Непараметрические критерии
Непараметрические критерии вычисляются проще, но они позволяют
оценить лишь средние тенденции, например, ответить на вопрос, чаще
ли в выборке А встречаются более высокие значения показателя, а выборке Б - более низкие.
Тем не менее, если непараметрические критерии показывают наличие различий - значит, эти различия действительно есть.
Однако если различия с помощью непараметрических методов не выявляются, то это еще не говорит о том, что их нет. Возможно, они есть, но для их выявления необходимо воспользоваться процедурой нормализации исходных распределений и соответствующими более мощными параметрическими критериями.
Слайд 12
Понятие одностороннего либо двустороннего критерия связано с формулировкой
гипотез.
Если нулевая гипотеза формулируется о равенстве (Х1 =
Х2), то для проверки используется двусторонний критерий.
Если нулевая гипотеза формулируется о неравенстве, то возможны следующие варианты:
если Х1Х2, то используется двусторонний критерий;
если Х1Х2 или Х1Х2, то односторонний критерий.
Слайд 13
Проверка гипотезы
Метод, который используется для принятия решения относительно
справедливости статистической гипотезы, называется проверкой гипотезы.
Основной принцип проверки
гипотезы состоит в том, что выдвигается нулевая гипотеза Но, с тем чтобы попытаться опровергнуть ее и тем самым подтвердить альтернативную гипотезу Н1.
При проверке любой статистической гипотезы решение исследователя никогда не принимается с уверенностью, поскольку всегда остается риск принятия неправильного решения. Поэтому в психолого-педагогических исследованиях при формулировке выводов и принятии решений всегда указывается степень их достоверности (уровень значимости).
Слайд 14
Принятие и отвержение гипотез
Для принятия или отвержения гипотез
в процессе формулирования статистического вывода необходимо знать: 1) эмпирическое
значение критерия, 2) его критические значения, 3) сам принцип принятия-отвержения гипотез.
Принцип принятия-отвержения гипотезы по А. Д. Наследову. Согласно ему, если эмпирическое значение критерия (коэффициента) превышает его критическое значение или равно ему, то отвергается Но и принимается Н1. В виде символов реализацию этого принципа можно записать следующим образом:
ЭМП ≥ КР => Н1,! на соответствующем уровне значимости
ЭМП<КР=> Но!
Для данных правил есть исключения. В случае реализации любого из этих принципов при работе с Т-критерием Вилкоксона, U-критерием Манна-Уитни и G-критерием знаков устанавливается обратное соотношение знаков < и >.
Слайд 15
Статистическая значимость
Уровень значимости (уровень достоверности) результата исследования (так
называемый p-уровень) – это вероятность того, что мы сочли
различия существенные, а они на самом деле случайны.
Значение p-уровня находится в обратной зависимости от надежности результата. Уровень значимости показывает вероятность ошибки при принятии гипотезы.
Уровень значимости – это вероятность отклонения нулевой гипотезы, в то время как она верна.
Например, р -уровень = 0,01 показывает, что имеется 1%-ная вероятность, что найденная в выборке связь между переменными является случайной и характерна только для данной выборки.
Слайд 16
Соотношение значимости и р - уровня
Слайд 17
Для каждого статистического критерия критические значения р- уровня
можно взять из соответствующих специальных таблиц.
Знание значения р
- уровня необходимо для подтверждения или опровержения статистических гипотез.
В психологии принято считать низшим уровнем статистической значимости 5%-ый уровень (р ≤ 0,05), достаточным - 1%-ый уровень (р ≤ 0,01) и высшим 0,1%-ый уровень значимости (р ≤ 0,001).
Результат р ≤ 0,05 большинством специалистов считается приемлемой границей статистической значимости.
Слайд 19
Число степеней свободы
Зная n и/или число степеней свободы,
по специальным таблицам можно определить критические значения критерия и
сопоставить с ними полученное эмпирическое значение.
В случае зависимых выборок число степеней свободы равно n-1.
Число степеней свободы для этих независимых выборок будет составлять (n1 + n2) - 2.
Слайд 20
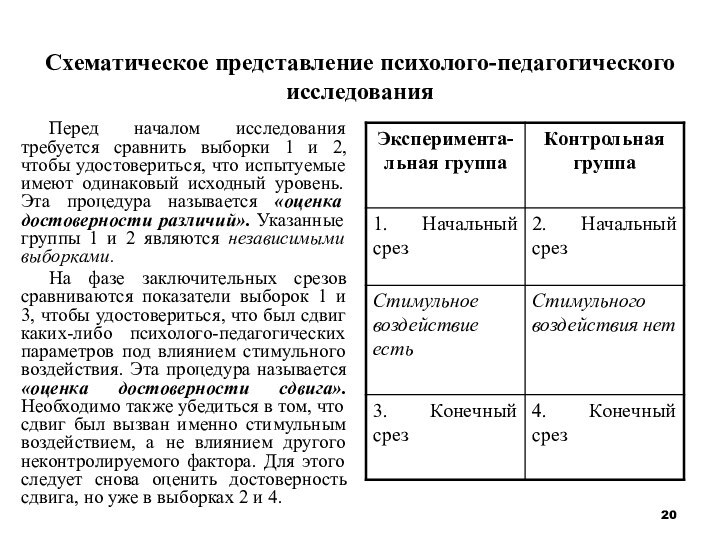
Схематическое представление психолого-педагогического исследования
Перед началом исследования требуется сравнить
выборки 1 и 2, чтобы удостовериться, что испытуемые имеют
одинаковый исходный уровень. Эта процедура называется «оценка достоверности различий». Указанные группы 1 и 2 являются независимыми выборками.
На фазе заключительных срезов сравниваются показатели выборок 1 и 3, чтобы удостовериться, что был сдвиг каких-либо психолого-педагогических параметров под влиянием стимульного воздействия. Эта процедура называется «оценка достоверности сдвига». Необходимо также убедиться в том, что сдвиг был вызван именно стимульным воздействием, а не влиянием другого неконтролируемого фактора. Для этого следует снова оценить достоверность сдвига, но уже в выборках 2 и 4.