- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Статистика
Содержание
- 2. Тема 4 Абсолютные, относительные и средние статистические показатели
- 3. Статистические показатели и их системаСтатистический показатель –
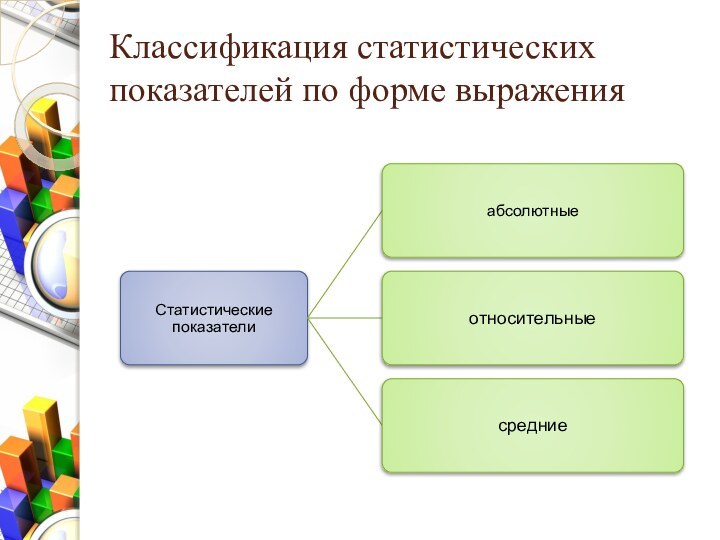
- 4. Классификация статистических показателей по форме выражения
- 5. Абсолютные статистические показателиАбсолютные показатели получают путем непосредственного
- 6. Измерители абсолютных показателей
- 7. Относительные статистические показателиОтносительный показатель представляет собой результат
- 8. Измерители относительных показателей
- 9. Виды относительных показателей
- 10. Относительные показатели динамикиОтносительные показатели динамики – отношение
- 11. Коэффициент роста и темп роста с переменной
- 12. Коэффициент роста и темп роста с постоянной базойгде уk – постоянная база сравнения.
- 13. Относительные показатели структурыОтносительные показатели структуры – характеризуют
- 14. Относительные показатели структуры (удельный вес)где уi – число единиц (или объем признака) по группе.
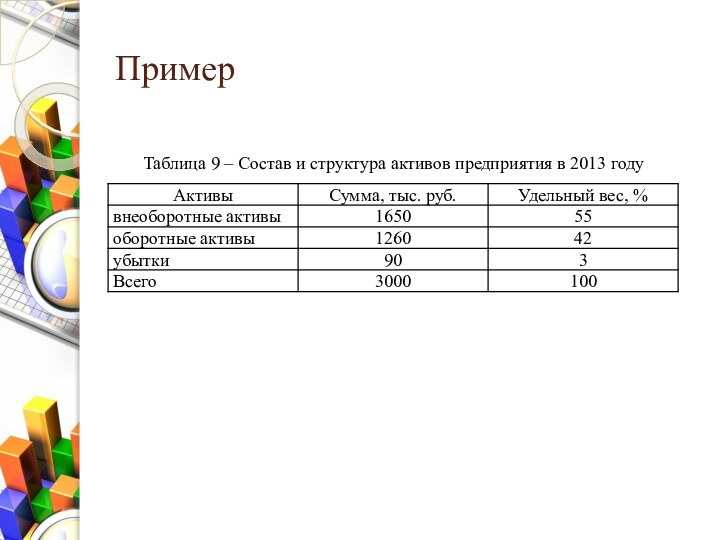
- 15. ПримерТаблица 9 – Состав и структура активов
- 16. Относительные показатели достижения уровняОтносительные показатели достижения уровня
- 17. Средние статистические показателиСредняя величина – это обобщенная
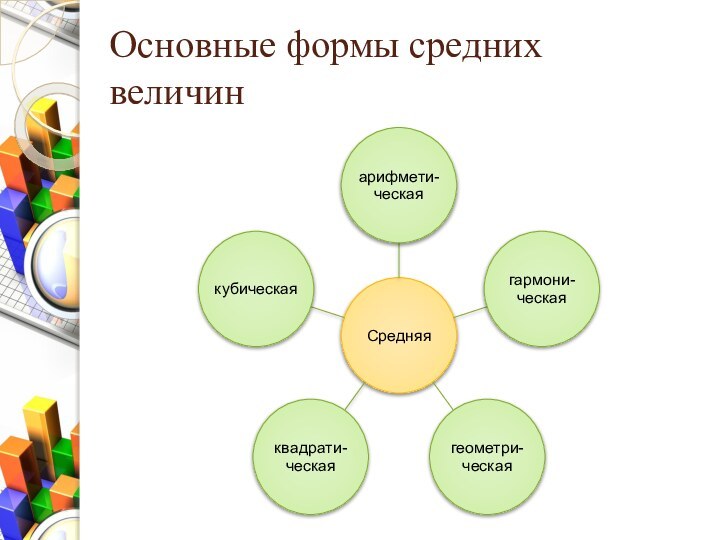
- 18. Основные формы средних величин
- 19. Формулы различных видов степенных средних величин
- 20. Условные обозначениягде – среднее значение признака;
- 21. Условия применения средней арифметической простойСредняя арифметическая простая
- 22. Условия применения средней арифметической взвешеннойСредняя арифметическая взвешенная
- 23. Условия применения средней гармонической взвешеннойСредняя гармоническая взвешенная
- 24. Условия применения средней геометрическойЕсли при замене индивидуальных
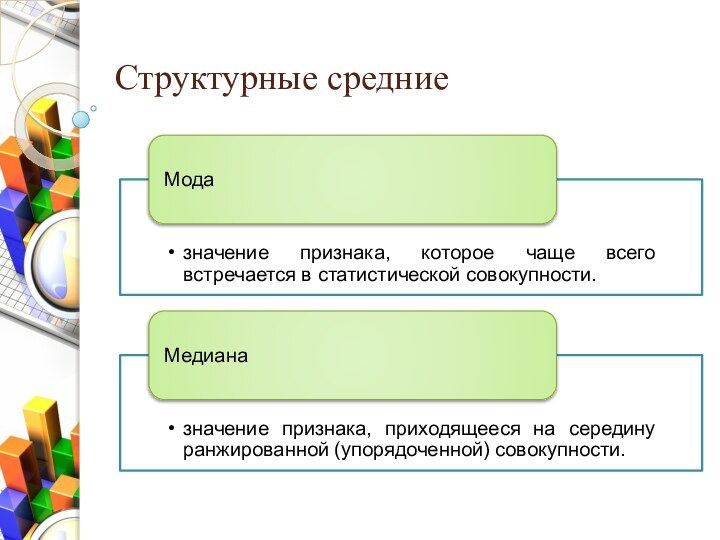
- 25. Структурные средние
- 26. МодаВ дискретном ряду мода определяется как значение
- 27. МедианаВ дискретном ранжированном вариационном ряду с нечетным
- 28. Тема 5 Статистические распределения и их основные характеристики
- 29. ВариацияРазличие значений признака у разных единиц совокупности
- 30. Классификация признаков
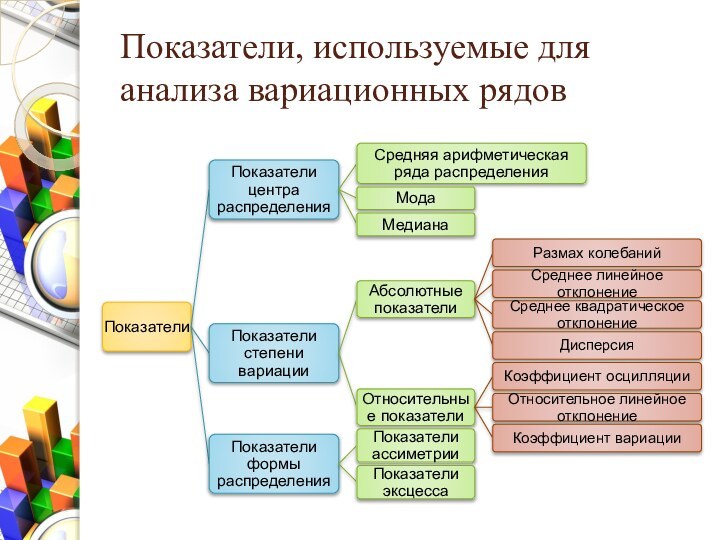
- 31. Показатели, используемые для анализа вариационных рядов
- 32. Абсолютные показатели степени вариации Размах колебаний:Среднее линейное отклонение:для несгруппированных данных:для сгруппированных данных:
- 33. Абсолютные показатели степени вариацииСреднее квадратическое отклонение (
- 34. Относительные показатели степени вариации Коэффициент осцилляцииОтносительное линейное отклонениеКоэффициент вариации
- 35. Сложение дисперсий изучаемого признакаОбщая дисперсияМежгрупповая дисперсияСредняя внутригрупповая дисперсияВзаимосвязь дисперсий – правило сложения дисперсий
- 36. Вариации альтернативного признакаАльтернативный признак – качественный признак,
- 37. Изучение форм распределенияЗакономерность распределения – закономерное изменение
- 38. Разновидности кривых распределения
- 39. Показатели формы распределенияОтносительный показатель асимметрии: (1) (2)Коэффициент асимметрии (средняя квадратическая ошибка):Показатель ассиметрии по Линдбергу:
- 40. Показатели формы распределенияПоказатель эксцесса (островершинности):Среднеквадратическая ошибка эксцесса:Величина эксцесса по Линдбергу:
- 41. Теоретическая частота нормального распределениянормальное(стандартизированное) отклонениеордината кривой нормального распределения – определяется по таблице значений функции
- 42. Скачать презентацию
- 43. Похожие презентации
Тема 4 Абсолютные, относительные и средние статистические показатели




































Слайд 3
Статистические показатели и их система
Статистический показатель – количественная
характеристика социально-экономических явлений и процессов в условиях качественной определённости.
статистических показателей – совокупность статистических показателей, всесторонне характеризующих социально-экономическое явление или процесс.
Слайд 5
Абсолютные статистические показатели
Абсолютные показатели получают путем непосредственного суммирования
первичных данных. Они характеризуют численность совокупности и объем (размер)
изучаемого явления (признака) в конкретных границах времени и места.Абсолютные показатели всегда являются именованными числами, то есть имеют какую-либо единицу измерения.
Слайд 7
Относительные статистические показатели
Относительный показатель представляет собой результат деления
одного абсолютного показателя на другой и выражает соотношение между
количественными характеристиками явлений и процессов.Абсолютный показатель в числителе называется текущим или сравниваемым. Абсолютный показатель в знаменателе называется основанием или базой сравнения.
Слайд 10
Относительные показатели динамики
Относительные показатели динамики – отношение уровня
явления в более позднее время (текущий период) к уровню
того же явления в более ранний (базисный) период.Такие показатели называют коэффициентами роста. Коэффициент роста выражается в коэффициентах. Если этот показатель выразить в процентах, то получим темп роста.
Коэффициент роста показывает, во сколько раз текущий уровень превышает базисный.
Темп роста характеризует сколько процентов составляет текущий (отчетный) уровень по отношению к базисному показателю.
Слайд 11
Коэффициент роста и темп роста
с переменной базой
где T –
относительный показатель динамики;
у1 , y2 , y3 , y4
, yп , yп+1 – значения уровня изучаемого явления, соответственно, в 1, 2, 3, 4, п-ом и (п+1) периодах.
Слайд 13
Относительные показатели структуры
Относительные показатели структуры – характеризуют долю
(удельный вес) части в целом. Например, отношение численности городского
населения к общей численности населения региона, страны.Относительные показатели структуры выражаются, как правило, в процентах или промилле.
Слайд 14
Относительные показатели структуры (удельный вес)
где уi – число единиц
(или объем признака) по группе.
Слайд 16
Относительные показатели достижения уровня
Относительные показатели достижения уровня –
характеризуют отношения фактически наблюдаемых величин признака к его нормативным,
плановым, оптимальным или максимально возможным величинам.Наиболее известной разновидностью таких показателей являются показатели выполнения плана, рассчитываемые как отношение фактических показателей изучаемого периода к плановым показателям этого же периода.
Слайд 17
Средние статистические показатели
Средняя величина – это обобщенная количественная
характеристика признака в статистической совокупности.
Она выражает характерную, типичную величину
признака у единиц совокупности, образующуюся в конкретных условиях места и времени под влиянием всех факторов.В средней величине признака взаимопогашаются индивидуальные различия признака, обусловленные действием случайных факторов.
Слайд 20
Условные обозначения
где – среднее значение признака;
xi – значения осредняемых признаков (
);fi – вес i-го варианта.
Слайд 21
Условия применения
средней арифметической простой
Средняя арифметическая простая применяется в
двух случаях: 1) когда данные статистического наблюдения не сгруппированы;
2) когда каждое значение признака встречается одинаковое количество раз.Т.е. среднюю арифметическую простую можно использовать только тогда, когда точно установлено отсутствие весов или их равенство.
Слайд 22
Условия применения
средней арифметической взвешенной
Средняя арифметическая взвешенная используется в
случае, когда статистические данные сгруппированы, и каждое значение признака
встречается неодинаковое количество раз.При расчете средней арифметической для интервального ряда распределения в качестве значений признака xi используют серединные значения интервалов, которые рассчитываются как среднеарифметическая его границ. Если интервал имеет открытую границу (это может быть верхний или нижний интервал), то серединное значение определяется исходя из предположения о равенстве интервала соседнему. Весами являются показатели численности каждой из групп.
Слайд 23
Условия применения
средней гармонической взвешенной
Средняя гармоническая взвешенная используется, когда
непосредственные данные о весах отсутствуют, а известны варианты осредняемого
признака x и произведения значений вариантов на количество единиц, имеющих данное его значение w (w=xf). В качестве весов в этом случае применяется не количество единиц совокупности с данным значением признака, а произведение этого количества на значения признака (w)
Слайд 24
Условия применения
средней геометрической
Если при замене индивидуальных значений признака
на среднее их значение необходимо сохранить неизменным произведение индивидуальных
значений, то используется средняя геометрическая.Средняя геометрическая чаще всего используется при определении средних темпов роста.
Слайд 26
Мода
В дискретном ряду мода определяется как значение признака
с наибольшей частотой.
В интервальном ряду для определения моды
сначала выявляется модальный интервал – интервал с наибольшей частотой. Внутри этого интервала находят точечную моду – условное значение признака, вблизи которого плотность распределения достигает максимума. Для расчета точечной моды используется формула:где х0 – нижняя граница модального интервала;
i – величина модального интервала;
fM0 – частота модального интервала;
fM0-1 – частота интервала, предшествующего модальному;
fM0+1 – частота интервала, следующего за модальным.
Слайд 27
Медиана
В дискретном ранжированном вариационном ряду с нечетным числом
единиц совокупности медианой является значение признака в центре ряда.
Если ранжированный ряд включает четное число единиц, то медиана определяется как средняя из двух центральных значений.В интервальном вариационном ряду основой для расчета точечного значения медианы служит медианный интервал. Медианный интервал определяется как первый интервал, накопленная частота (то есть сумма частот всех предыдущих интервалов и данного интервала) которого превышает половину общей суммы частот. Для нахождения медианы применяется формула:
где х0 – нижняя граница медианного интервала;
i – величина медианного интервала;
SMe – накопленная частота интервала, предшествующего медианному интервалу;
fMe – частота медианного интервала.
Слайд 29
Вариация
Различие значений признака у разных единиц совокупности в
статистике называется вариацией.
Вариационный ряд – групповая таблица, построенная
по количественному признаку, в сказуемом которой показывается число единиц в каждой группе.
Слайд 32
Абсолютные показатели степени вариации
Размах колебаний:
Среднее линейное отклонение:
для несгруппированных
данных:
для сгруппированных данных:
Слайд 33
Абсолютные показатели степени вариации
Среднее квадратическое отклонение ( )
и дисперсия ( ):
для несгруппированных данных
для сгруппированных данных
Преобразованная
формула дисперсии
Слайд 34
Относительные показатели степени вариации
Коэффициент осцилляции
Относительное линейное отклонение
Коэффициент
вариации
Слайд 35
Сложение дисперсий изучаемого признака
Общая дисперсия
Межгрупповая дисперсия
Средняя внутригрупповая дисперсия
Взаимосвязь
дисперсий – правило сложения дисперсий
Слайд 36
Вариации альтернативного признака
Альтернативный признак – качественный признак, имеющий
две взаимоисключающие разновидности.
Он имеет только два значения:
1 – наличие
признака;0 – отсутствие признака
Среднее значение альтернативного признака:
Дисперсия альтернативного признака:
где p – доли единиц, обладающих признаком
q – доли единиц, не обладающих признаком





























