- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тема заняття
Содержание
- 2. Мета заняттяСформувати: поняття про алгоритм, властивості алгоритмів,
- 3. Зміст матеріалу: 1. Поняття алгоритму. Приклади. 2. Виконавці
- 4. Поняття алгоритму Термін алгоритм існував задовго
- 5. Виконавці алгоритмів Вчинки людей підпорядковані
- 6. Способи опису алгоритмів Є такі способи
- 7. Властивості алгоритмів Існують такі властивості алгоритмів:-
- 8. Поняття величини Властивості будь-якого об’єкта, що вивчається, описують
- 9. Величини в програмуванні У програмуванні поняття величини
- 10. Величини в алгоритмах Змінні можуть набувати різних значень.
- 11. Величини в алгоритмах Для створення імен можна застосовувати
- 12. Схема алгоритму Одним із способів опису алгоритмів є
- 13. Основні конструкції алгоритмів Існують такі алгоритмічні конструкції: 1) лінійна (послідовність простих команд); 2) розгалужена (розгалужені алгоритми); 3) циклічна (циклічні алгоритми).
- 14. Лінійні алгоритми Якщо алгоритм складається лише
- 15. Розгалужені алгоритми1) Повна форма команди розгалуження: якщо
- 16. Умовна команда – це
- 17. Циклічні алгоритми Циклічними називаються алгоритми, які містять команди,
- 18. Циклічні алгоритми 1) Цикл з післяумовою
- 19. Розглянемо таке завдання.Біля крана з водою є
- 20. Алгоритм рішення цього завдання можна скласти й
- 21. 3) Цикл з параметром (цикл із заздалегідь
- 22. Команда працює в такий спосіб:1. Керуюча змінна
- 23. Розглянемо те ж завдання:Біля крана з водою
- 24. . I=j,kJ=1; k=10Початок1. Чому не вказаний в
- 25. . I=j,k,mj=mk,mПочатокЩо позначено буквами k, m?
- 26. . k – місткість бочки;m – місткість
- 27. Задача1. Скласти алгоритм знаходження більшого з двох
- 28. Величини, які описані в допоміжному алгоритмі і
- 29. Поняття про мови програмування Мова — це
- 30. Алгоритмічна мова — це мова, призначена для
- 31. Мови програмування — це алгоритмічні мови, призначені
- 32. Програма — це алгоритм, записаний мовою програмування.Транслятор
- 33. Інтерпретація (від англ. interpretation) — спосіб трансляції,
- 34. Компіляція (від англ. compile — збирати) —
- 35. Класифікація мов програмуванняМови програмування високого і низького
- 36. Класифікація мов програмуванняМови програмування високого і низького
- 37. Класифікація мов програмуванняМови програмування високого і низького
- 38. Класифікація мов програмування Процедурні і непроцедурні мови.
- 39. Системи програмування. Для зручності створення програм
- 40. Системи програмування. Отримали поширення системи візуального програмування
- 41. Розв’язання задач у будь-якій діяльності людини –
- 42. При постановці задачі необхідно визначити і перелічити
- 43. Означення. Інформаційна модель – це такий матеріальний
- 44. Означення. Математична модель – заміна оригіналу або
- 45. Постановка задачі та її змістовний аналізВизначити умову
- 46. Формалізація задачі, вибір методу її розв’язування Розгорнути
- 47. Складання алгоритму на основі обраного методуАлгоритм більшою
- 48. Складання програмиПрограмування (складання програми) – кодування складеного
- 49. Тестування та налагодження програмиПеревірка правильності роботи програми
- 50. Скачать презентацию
- 51. Похожие презентации












































Слайд 2
Мета заняття
Сформувати: поняття про алгоритм, властивості алгоритмів, програму,
мову програмування.
Етапи розв’язування задач за допомогою комп’ютера
Слайд 3
Зміст матеріалу:
1. Поняття алгоритму. Приклади.
2. Виконавці алгоритмів.
3.
Способи опису алгоритмів.
4. Властивості алгоритмів.
5. Схема алгоритму.
6. Основні конструкції
алгоритмів (лінійні, розгалужені, циклічні). Приклади.А л г о р и т м и
Слайд 4
Поняття алгоритму
Термін алгоритм існував задовго до
появи комп’ютерів. Він походить від імені давнього філософа
і математика з Хорезму (Узбекистан), що жив у 9 ст. Мухаммед аль-Хорезмі. Саме він у своїх трактатах описав правила (алгоритми) додавання, віднімання, множення і ділення багатозначних чисел, якими ми користуємося сьогодні.Алгоритм – зрозуміле і точне розпорядження виконавцю виконати послідовність дій, спрямованих на досягнення зазначеної мети чи на розв'язання поставленої задачі.
Приклади:
Завдання: Обчислити
360
92 - 32
Алгоритм виконання:
Виконати віднімання 92 – 32 і запам’ятати результат 60.
Виконати ділення 360 : 60 і запам’ятати результат 6.
Завдання: Закип’ятити воду.
Алгоритм Кип’ятіння води
1. Налити в чайник води. 2. Запалити плитку.
3. Поставити чайник на плитку. 4. Чекати поки вода закиппть.
5. Зняти чайник з плитки. 6. Виключити плитку.
Слайд 5
Виконавці алгоритмів
Вчинки людей підпорядковані досягненню
конкретної мети. Обдумуючи план на день, ми складаємо алгоритми
розв’язування побутових чи профе-сійних задач. Отже, людина є виконавцем алгоритмів.Для полегшення фізичної та інтелектуальної праці люди створили різні технічні пристрої: машини, роботи, автомати, комп’ютери.
Кожен виконавець може виконати певну кількість команд, які називають-ся допустимими командами виконавця.
Розглянемо таких виконавців: людину, робота, комп’ютер.
1. Людина здатна виконати практично необмежену кількість різних ко-манд: іти, лічити, шити, їсти, спати і т.д. Тому на дії людей розумні обмеже-ння накладаються законами, мораллю й сумлінням.
2. Кількість команд для робота є значно меншою. Наприклад, уперед, направо і т.д. – це допустимі команди робота. Але робот не виконає таких команд: їсти, пити, спати.
3. Додавати, віднімати, множити, ділити, малювати, грати – це команди для комп’ютера, але він не може виконати команду, наприклад, переміще-ння у просторі, яка характерна для людини і робота.
Команди, які не може виконати виконавець, називаються недопустимими командами виконавця.
Слайд 6
Способи опису алгоритмів
Є такі способи опису
алгоритмів:
1) словесно-формульний (описували алгоритми при розгляді прикл. 1
і 2)2) графічний у вигляді блок-схем;
3) алгоритмічною мовою або мовою програмування.
Будемо вчитися описувати алгоритм мовою програмування, а не алго-ритмічною мовою, тому що правильність алгоритму (програми) записаної на мові програмування можна перевірити лише за допомогою комп’ютера.
Наведемо приклад словесного способу опису алгоритмів. Алгоритмові дає-мо назву, команди нумеруємо. Назву пишемо з великої літери.
Приклад:
3) Завдання: Скласти алгоритм переходу вулиці.
Алгоритм Перехід
1. Подивитися наліво.
2. Якщо немає перешкоди, то йти до середини вулиці, інакше пропусти-ти машини і йти до середини вулиці.
3. Подивитися направо.
4. Якщо немає перешкоди, то завершити перехід, інакше пропустити ма-шини і завершити перехід.
Дайте відповіді на запитання:
1. Хто може бути виконавцем цього алгоритму?
2. Чи можна в алгоритмі поміняти будь-які дві команди місцями, чи буде новий алгоритм правиль-ний?
Слайд 7
Властивості алгоритмів
Існують такі властивості алгоритмів:
- Визначеність
алгоритму
Алгоритм визначений, якщо він складається з
допустимих команд виконавця, які можна виконати для зазначених вхідних даних. Невизначеність, наприклад, виникне в алгоритмі прикладу 1, якщо в знаменнику буде записано 92-92 (ділення на 0 не допустиме).- Скінченність алгоритму
Послідовність команд, які потрібно виконати, має бути скінченною.
Алгоритм прикладу 1 – скінченний. Він складається з трьох дій.
Нескінченний, наприклад, алгоритм обчислення ділення 5 : 3.
- Результативність алгоритму
Алгоритм результативний, якщо він дає результати. Наведені вище алгоритми є результативними.
- Правильність алгоритму
Алгоритм правильний, якщо його виконання забезпечує досягнення мети. Якщо в алгоритмі прикладу 3 поміняти місцями пункти 1 і 2 або 3 і 4, то отримаємо неправильний алгоритм.
- Формальність алгоритму
Якщо алгоритм можуть виконати не один, а декілька виконавців і одержати однакові результати.
- Масовість алгоритму
Алгоритм масовий, якщо він придатний для розв’язування не однієї задачі, а низки подібних задач. Алгоритм прикладу 1 немасовий, а прикладу 3 (перехід вулиці) – масовий.
Приклад масовості алгоритму:
Написати алгоритм розв’язування лінійного рівняння ах+в=с, де а, в та с – будь-які числа і а≠0.
Слайд 8
Поняття величини
Властивості будь-якого об’єкта, що вивчається, описують за
допомогою величин.
Поняття величини прийшло до нас із математики.
Вперше властивості величини чітко були сформульовані Евклідом у його «Початках» (III ст. до н.е.). З давніх часів величина розглядалася як узагальнення конкретних понять: довжини, площі, об'єму, маси тощо. Величини служили людям для опису об'єктів і процесів у матеріальному світі. За допомогою величин можна виразити довжину відрізка, площу земельної ділянки, висоту будинку, швидкість пішохода або автомобіля, час обертання планети навколо Сонця. З прикладами величин ви зустрічаєтеся щодня: відстань між будинком і магазином, температура повітря тощо. Кожний розмір характеризується певним значенням, наприклад, швидкість може дорівнювати 80км/год, відстань — 700м, а температура — 15°С.
Слайд 9
Величини в програмуванні
У програмуванні поняття величини дещо
відрізняється від поняття величини у природничих науках. Воно є
формальнішим: величиною називають об'єкт, з яким пов'язується певна множина значень. Такому об'єкту надається оригінальне ім'я –ідентифікатор.У програмуванні величини використовують для опису потрібних дій. Усі величини в програмі (алгоритмі) поділяють на сталі (або константи) і змінні. Константи не можуть змінювати свої значення в процесі виконання алгоритму.
Приклади констант: π=3,14; ρ=1000; t=60.
Слайд 10
Величини в алгоритмах
Змінні можуть набувати різних значень. Змінна
зберігає надане їй значення, доки не отримає нового.
Приклади
використання змінних величин: a=5x-7; i=i+3.Змінним величинам обов’язково призначають імена. Отже, змінна — це іменована величина, яка в процесі виконання алгоритму може набувати і зберігати різні значення. Імена змінних вибирають так, щоб вони співпадали із звичайними позначеннями відповідних величин або нагадували смисл змінної. Імена змінних мають бути різними між собою і не співпадати з будь-яким службовим словом мови. В алгоритмі не можуть існувати різні об’єкти з однаковими іменами. Усі імена є унікальними.
Слайд 11
Величини в алгоритмах
Для створення імен можна застосовувати тільки
латинські літери, цифри, знак підкреслення. Імена обов’язково розпочинаються з
літери. Великі й малі літери в іменах не розрізняються. Ніякі верхні чи нижні індекси не застосовуються. Наприклад, значення висоти конуса можна зберігати в змінній з іменем h, значення його об’єму — в змінній V, а для кута при вершині можна вибрати змінну з іменем alpha.Допустимі імена величин: А, а, Аа, аА, ав, а25, а_25, В46р, kvadrat
Недопустимі імена величин: 4АР67, 34+а, 25a, 2a5
Слайд 12
Схема алгоритму
Одним із способів опису алгоритмів є графічний,
тобто за допомогою блок-схем. На такій схемі операції виконавця
подаються блоками і з’єднані між собою стрілками. Є різні позначення блоків в залежності від конкретних дій.прямокутник - арифметичний блок, в який записується математична формула, наприклад, а=b+с; D=b2-4ac і т.д.
В таких блоках знак “=“ – це знак присвоєння, іноді його записують так “:=”.
ромб – логічний блок, в який записується умова.
Наприклад, а>b, D≥0 і т.д.
паралелограм - в який записуються дані, які вводяться і виводяться з алгоритму.
еліпс - записують початок і кінець алгоритму.
шестикутник - запис умови циклу з параметром
Слайд 13
Основні конструкції алгоритмів
Існують такі алгоритмічні конструкції:
1) лінійна (послідовність
простих команд);
2) розгалужена (розгалужені алгоритми);
3) циклічна (циклічні алгоритми).
Слайд 14
Лінійні алгоритми
Якщо алгоритм складається лише з
послідовності простих команд, то його називають лінійним.
Наприклад: Знайдіть значення
виразу z = x-5y+10, де y = 3x+4Блок-схема має вигляд:
Слайд 15
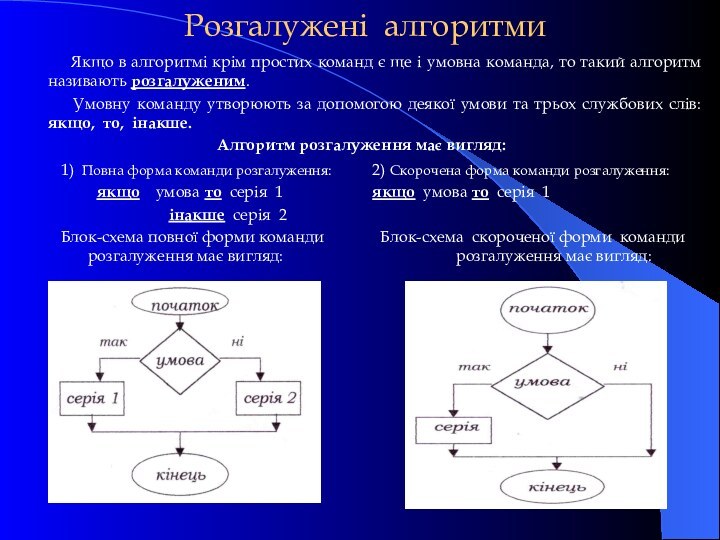
Розгалужені алгоритми
1) Повна форма команди розгалуження:
якщо
умова то серія 1
інакше серія
2Блок-схема повної форми команди розгалуження має вигляд:
2) Скорочена форма команди розгалуження:
якщо умова то серія 1
Блок-схема скороченої форми команди розгалуження має вигляд:
Якщо в алгоритмі крім простих команд є ще і умовна команда, то такий алгоритм називають розгалуженим.
Умовну команду утворюють за допомогою деякої умови та трьох службових слів: якщо, то, інакше.
Алгоритм розгалуження має вигляд:
Слайд 16 Умовна команда – це вказівка
виконати одну з двох команд: команду 1 (серія 1),
якщо умова справджується, або команду 2 (серія 2), якщо умова не справджується. Замість однієї команди може бути серія команд.Приклад: Знайти корені квадратного рівняння a x2+bx+c=0, де a, b, c > 0.
Словесний спосіб опису алгоритму:
Алгоритм Розв’язки квадратного рівняння
1. Обчислити D=b2-4ac
2. Якщо D<0, то “рівняння розв’язку немає”
3. Якщо D>0, то
4. Якщо D=0, то x=x1=x2=-b/2a
Блок-схема має вигляд:
Слайд 17
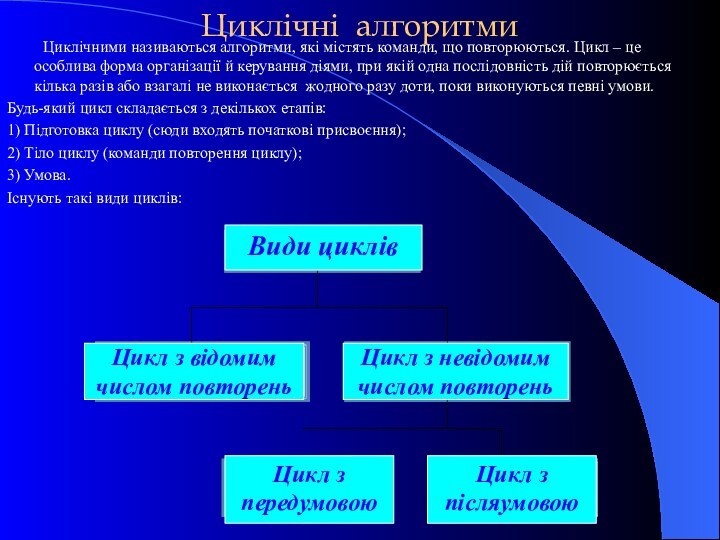
Циклічні алгоритми
Циклічними називаються алгоритми, які містять команди, що
повторюються. Цикл – це особлива форма організації й керування
діями, при якій одна послідовність дій повторюється кілька разів або взагалі не виконається жодного разу доти, поки виконуються певні умови.Будь-який цикл складається з декількох етапів:
1) Підготовка циклу (сюди входять початкові присвоєння);
2) Тіло циклу (команди повторення циклу);
3) Умова.
Існують такі види циклів:
Види циклів
Цикл з відомим числом повторень
Цикл з невідомим числом повторень
Цикл з передумовою
Цикл з післяумовою
Слайд 18
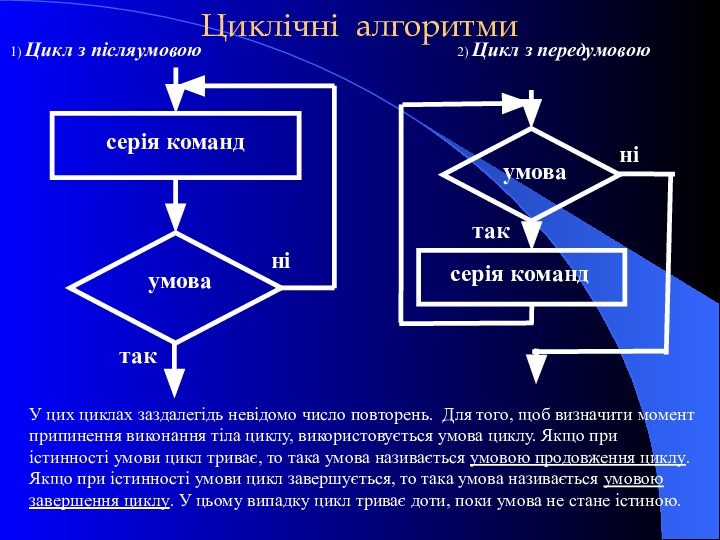
Циклічні алгоритми
1) Цикл з післяумовою
2) Цикл з передумовою
У цих циклах заздалегідь невідомо число повторень. Для того, щоб визначити момент припинення виконання тіла циклу, використовується умова циклу. Якщо при істинності умови цикл триває, то така умова називається умовою продовження циклу.
Якщо при істинності умови цикл завершується, то така умова називається умовою завершення циклу. У цьому випадку цикл триває доти, поки умова не стане істиною.
Слайд 19
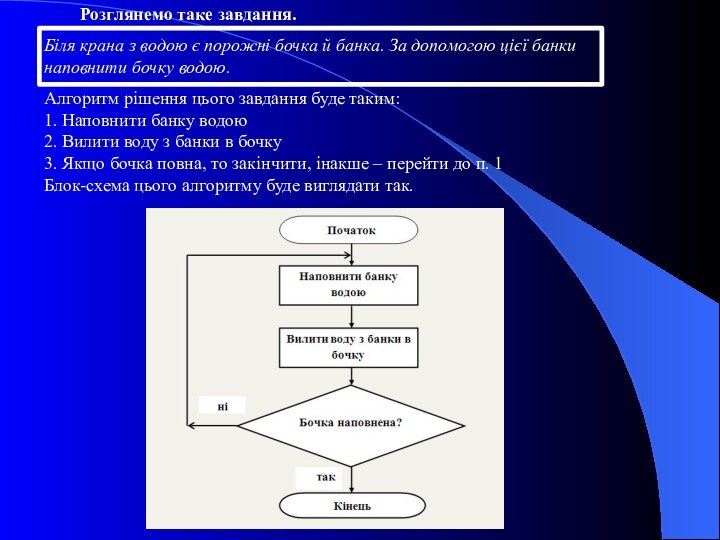
Розглянемо таке завдання.
Біля крана з водою є порожні
бочка й банка. За допомогою цієї банки наповнити бочку
водою.Алгоритм рішення цього завдання буде таким:
1. Наповнити банку водою
2. Вилити воду з банки в бочку
3. Якщо бочка повна, то закінчити, інакше – перейти до п. 1
Блок-схема цього алгоритму буде виглядати так.
Слайд 20
Алгоритм рішення цього завдання можна скласти й інакше.
Блок-схема
має вигляд:
Відмінність цих алгоритмів полягає в тому, що в
першому алгоритмі команди Наповнити банку й Вилити воду з банки в бочку виконуються до перевірки умови, а в другому – після перевірки умови. У першому алгоритмі команди циклу Наповнити банку й Вилити воду з банки в бочку будуть виконуватися хоча б один раз, а в другому – можуть не виконуватися жодного разу (це буде в тому випадку, коли перед початком виконання алгоритму бочка вже повна).Слайд 21 3) Цикл з параметром (цикл із заздалегідь відомим
числом повторень) –використовується тоді, коли число повторень тіла циклу
заздалегідь відомо. Наприклад, 10 разів написати слово «привіт» або 100 разів сказати «Я так більше не буду». Він має такий вигляд:де І — керуюча змінна циклу (параметр);
j — початкове значення І;
k — кінцеве значення І;
т — значення кроку зміни І. Якщо значення кроку зміни І дорівнює одиниці, то його можна опускати;
j, k, m — у загальному випадку можуть бути виразами.
серія команд
Слайд 22
Команда працює в такий спосіб:
1. Керуюча змінна І
(змінна циклу) на початку набуває значення j і здійснюється
перевірка, чи значення змінної І не дорівнює значенню k; якщо умова «істинна», то виконуються команди циклу.2. Потім, щоразу до керуючої змінної І додається значення кроку m і здійснюється перевірка , чи значення змінної І не дорівнює значенню k; якщо умова «істинна», то виконуються команди циклу.
3. Виконання серії циклу відбувається тільки після виконання однієї з умов:
i≤k, якщо крок додатний;
i≥k, якщо крок від'ємний.
4. При невиконанні умови відбувається вихід з циклу.
Слайд 23
Розглянемо те ж завдання:
Біля крана з водою є
порожні бочка й банка. За допомогою цієї банки наповнити
бочку водою.Яким буде алгоритм рішення завдання цього разу?
Параметр циклу повинен рахувати кількість банок або кількість літрів. Під час рахунку кількості банок параметр змінює своє значення на одиницю. А під час рахунку кількості літрів параметр може змінювати своє значення з довільним кроком: 1, 2, 3, 4 і т.д.
Слайд 24
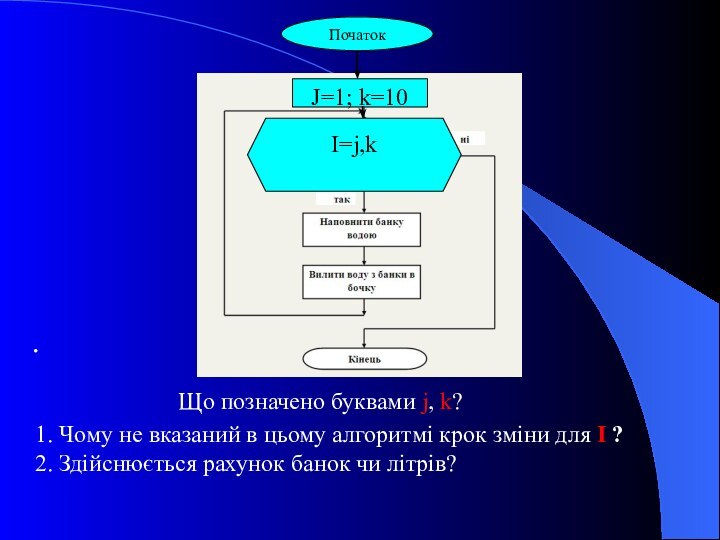
.
I=j,k
J=1; k=10
Початок
1. Чому не вказаний в цьому
алгоритмі крок зміни для І ?
2. Здійснюється рахунок
банок чи літрів?Що позначено буквами j, k?
Слайд 26
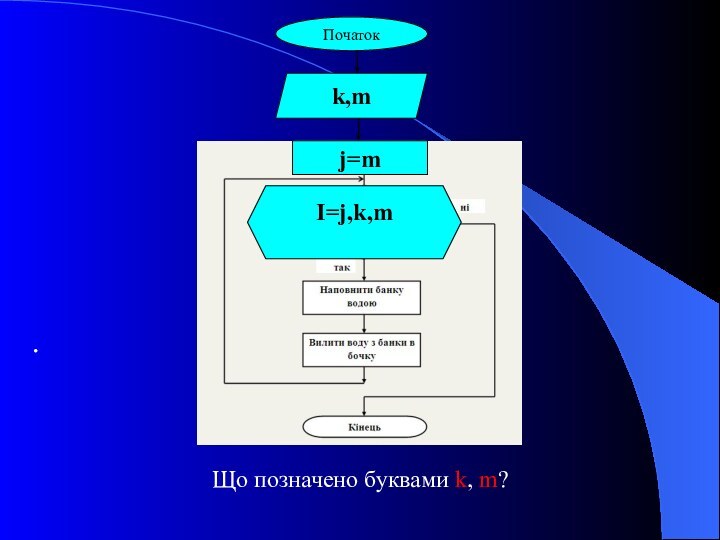
.
k – місткість бочки;
m – місткість банки
Яке
початкове значення І?
На скільки змінюється І?
При якому кінцевому значенні
І буде наповнюватись бочка?Яке кінцеве значення І?
j=m
Слайд 27 Задача1. Скласти алгоритм знаходження більшого з двох натуральних
чисел Х і У.
Алгоритм Bid
1. Порівняти два числа Х
і У2. Результату Z надати значення більшого числа
Задача2. Скласти алгоритм знаходження більшого з трьох натуральних чисел А, В, С.
Алгоритм Bit
1. Порівняти два числа А і В
2. Результату Z надати значення більшого числа
3. Порівняти два числа Z і C
4. Результату Z надати значення більшого числа
В алгоритмі Bit виконуються ті самі дії, що і в алгоритмі Bid. Тому алгоритм Bid можна використати як допоміжний (до нього можна написати звернення в алгоритмі Bit).
Отже, допоміжний алгоритм – це алгоритм, який вирішує частину завдання й викликається з основної програми
Допоміжні алгоритми
Слайд 28 Величини, які описані в допоміжному алгоритмі і використовуються
тільки в ньому, називаються
локальними.
Величини, які описані в
основному алгоритмі, але використовуються і в основному алгоритмі, і в допоміжних алгоритмах , називаютьсяглобальними
Допоміжні алгоритми
Слайд 29
Поняття про мови програмування
Мова — це система
знаків (символів, жестів, міміки, положень перемикача і т. д.)
для представлення, обміну інформацією. Це загальне визначення включає в себе і природні, і штучні (формальні) мови. До штучних мов належать мови, створені людьми для розв’язання специфічних задач. Це мова математичних формул, нотна грамота, мови програмування тощо.Основи програмування
Слайд 30 Алгоритмічна мова — це мова, призначена для представлення
алгоритму у вигляді послідовності вказівок для виконання їх виконавцем
алгоритму.Алгоритмічна мова, як і кожна інша, має свій словник. Основу цього словника складають слова, що використовуються для запису команд, які входять у систему команд виконавця.
Основи програмування
Слайд 31 Мови програмування — це алгоритмічні мови, призначені для
опису алгоритмів, що орієнтовані для виконання на комп’ютері, або
система позначень для точного опису алгоритму, який треба виконати за допомогою комп’ютера.Мова програмування, як і будь-яка інша мова, являє собою набір символів (алфавіт), систему правил складання базових конструкцій мови (синтаксис) та правила тлумачення мовних конструкцій (семантика). Ця система позначень і правил призначена для одноманітного і точного запису алгоритму. Алфавіт, синтаксис і семантика — три основні складові мов програмування.
Основи програмування
Слайд 32
Програма — це алгоритм, записаний мовою програмування.
Транслятор (від
англ. translation — переклад) — програма, яка перетворює команди
мови програмування на машинну мову. Існує два способи трансляції: інтерпретація та компіляція.Основи програмування
Слайд 33 Інтерпретація (від англ. interpretation) — спосіб трансляції, при
якому кожна інструкція програми перекладається в машинні коди та
виконується, і тільки після виконання одного фрагмента програми процесор переходить до обробки іншого фрагмента. Це гнучка система перекладу, яка реалізовується нескладно. Вона використовується в тих випадках, коли потрібна простота трансляції (Basic), або там, де інший спосіб перекладу дуже складний або навіть неможливий (Lisp).Основи програмування
Слайд 34 Компіляція (від англ. compile — збирати) — спосіб
трансляції, при якому здійснюється переклад усього тексту програми, збір
перед її виконанням та запис у пам’ять комп’ютера.При перегляді програми компілятор виділяє місце в пам’яті комп’ютера для кожної змінної.
Основи програмування
Слайд 35
Класифікація мов програмування
Мови програмування високого і низького рівнів.
Програми для перших ЕОМ складалися машинною мовою, вельми далекою
від понять, якими оперує людина.Алфавіт машинної мови складається тільки з двох символів {0, 1}. Для складання програм на такій мові була потрібна досить висока кваліфікація. Програмісти, зацікавлені в полегшенні своєї праці, і виробники ЕОМ зацікавлені в розширенні ринку, стали шукати вихід. Першим кроком на шляху створення мов, що містять поняття, близькі поняттям людини, стали мови, що перекладають символічні імена в машинні коди
Основи програмування
Слайд 36
Класифікація мов програмування
Мови програмування високого і низького рівнів.
До
мов програмування низького рівня належать мови асемблера — машинно-залежні
мови, що описують дії в термінах команд процесора. Для кожного типу процесора існує своя мова асемблера, тому для перенесення програми на асемблері на іншу апаратну платформу її потрібно майже повністю переписати.Основи програмування
Слайд 37
Класифікація мов програмування
Мови програмування високого і низького рівнів.
Пізніше були створені програми, що транслюють арифметичні вирази (автокоди),
і, нарешті, у 1958 році вступив у дію транслятор Фортрана — першої мови високого рівня (МВР). Мови високого рівня наближені до природних понять. Ці мови є машинно-незалежними. Із розвитком і поширенням комп’ютерів намітився двоякий процес: поява спеціальних (Пролог) та універсальних (Паскаль, Сі) мов.Основи програмування
Слайд 38
Класифікація мов програмування
Процедурні і непроцедурні мови.
Програма,
написана процедурною мовою, описує, як розв’язувати, використовуючи при цьому
такі основні поняття, як слідування, розгалуження, цикл. Програма, написана непроцедурною мовою, описує, що робити, використовуючи такі поняття, як підстановка, галуження, рекурсія.Основи програмування
Слайд 39
Системи програмування.
Для зручності створення програм створюються
інтегровані середовища програмування — системи, які об’єднують редактор текстів
програм, транслятор, налагоджувач (наприклад Turbo Pascal, Turbo С, Turbo Basic).Основи програмування
Слайд 40
Системи програмування.
Отримали поширення системи візуального програмування —
засоби, за допомогою яких можна швидко створювати програми шляхом
візуального проектування макета в графічному вигляді (наприклад, Visual Basic, Visual С, Delphi).Основи програмування
Слайд 41
Розв’язання задач у будь-якій діяльності людини – це
завжди одержування певних результатів – результатів обчислень, побудови, роботи
тощо.Етапи розв’язання задач на комп’ютері:
Математична постановка задачі
Визначення методів розв’язання
Складання сценарію роботи з комп’ютером
Конструювання алгоритму
Переведення алгоритму у програму
Введення і випробування програми
Одержання результатів для даного способу розв’язання
Основні поняття
Слайд 42
При постановці задачі необхідно визначити і перелічити всі
вихідні дані і дані, які необхідно знати.
Означення. Моделювання –
це особлива форма експерименту, яка полягає в тому, що досліджується не сам об’єкт, певна його заміна.Форми моделювання є дуже різноманітними і залежать як від самого об’єкта, так і від мети його вивчення.
Основні поняття
Слайд 43
Означення. Інформаційна модель – це такий матеріальний або
уявний об’єкт, що використовується замість об’єкта-оригіналу або явища (процесу)
під час цього дослідження, при цьому зберігається інформація про певні важливі для даного дослідження типові риси і властивості оригіналу, тобто його суттєві сторони.Основні поняття
Слайд 44
Означення. Математична модель – заміна оригіналу або явища
(процесу) відповідним аналогом за допомогою математичних залежностей.
Розв’язання практичної задачі
починається з опису вихідних даних і мети задачі. Точне формулювання умов і мети розв’язання задачі – це математична постанова задачі, а математичний опис найсуттєвіших властивостей реального об’єкта – це математична модель.Основні поняття
Слайд 45
Постановка задачі та її змістовний аналіз
Визначити умову задачі:
що дано? що необхідно? які дані припущення? які результати
і в якому вигляді мають бути отримані?Провести змістовний аналіз спрямований на уточнення мети розв’язання задачі, її смислових компонентів, вихідних даних.
Визначити, за яких умов можливо отримання необхідних результатів, а за яких – ні.
Визначити, які результати вважатимуться вірними.
Етапи розв’язання прикладних задач з використанням комп’ютера
Слайд 46
Формалізація задачі, вибір методу її розв’язування
Розгорнути змістовний
опис задачі, замінити її математичною моделлю за допомогою математичних
залежностей.Обґрунтовано обрати метод розв’язання задачі.
Етапи розв’язання прикладних задач з використанням комп’ютера
Слайд 47
Складання алгоритму на основі обраного методу
Алгоритм більшою мірою
визначається обраним методом, хоча один і той самий метод
може бути реалізований за допомогою різних алгоритмів. Під час складання алгоритму враховувати всі його властивості.Етапи розв’язання прикладних задач з використанням комп’ютера
Слайд 48
Складання програми
Програмування (складання програми) – кодування складеного алгоритму
однією з мов програмування.
Етапи розв’язання прикладних задач з використанням
комп’ютера
Слайд 49
Тестування та налагодження програми
Перевірка правильності роботи програми за
допомогою тестів і виправлення виявлених похибок.
Тест – це спеціально
підібрані вхідні дані та результати, отриманні за цих даних.Етапи розв’язання прикладних задач з використанням комп’ютера





























