Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Теорема Эйлера

Содержание

Историческая справкаТеорема Эйлера- математическое утверждение, связывающее между собой число ребер, граней и вершин многогранников.Теорема Эйлера была открыта французским ученым Рене Декартом еще в 1640 году, затем забыта более чем на сто лет и лишь в 1752
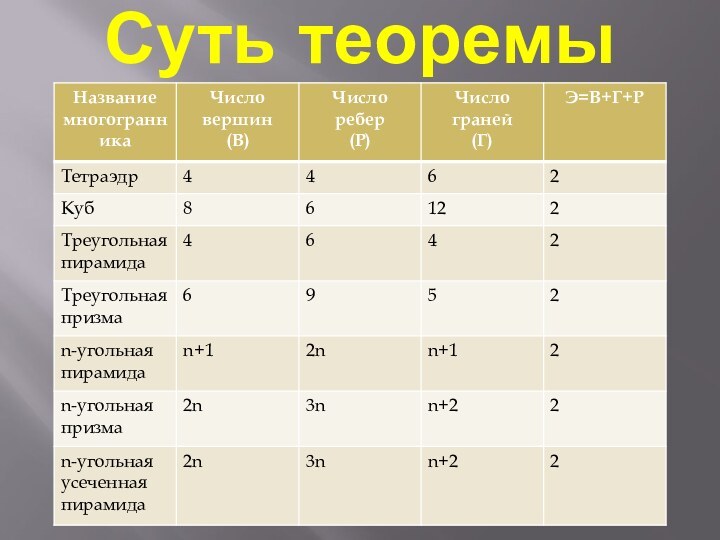
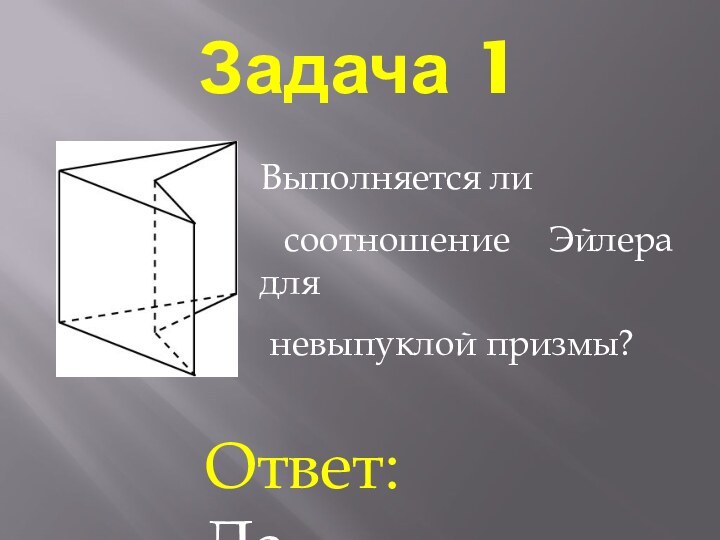
Теорема ЭйлераПодготовили: Богодухова Марина Историческая справкаТеорема Эйлера- математическое утверждение, связывающее между собой число ребер, граней и Леонард Эйлер (1707-1783) — математик, физик механик и астроном. Суть теоремы Теорема ЭйлераДля любого выпуклого многогранника число вершин (В), число рёбер (Р) и Задача 1Выполняется ли соотношение Эйлера для невыпуклой призмы?Ответ: Да. Задача 2Посчитайте число вершин (В), ребер (Р) и граней (Г) у многогранников, Чему равна эйлерова характеристика многогранника (В – Р + Г), где В
Слайды презентации

Слайд 2 Историческая справка
Теорема Эйлера- математическое утверждение, связывающее между собой

Историческая справкаТеорема Эйлера- математическое утверждение, связывающее между собой число ребер, граней

число ребер, граней и вершин многогранников.
Теорема Эйлера была открыта

французским ученым Рене Декартом еще в 1640 году, затем забыта более чем на сто лет и лишь в 1752 году переоткрыта математиком Леонардом Эйлером, имя которого она носит.

Слайд 3 Леонард Эйлер (1707-1783)
— математик, физик механик и астроном.

Леонард Эйлер (1707-1783) — математик, физик механик и астроном.

Слайд 4 Суть теоремы

Суть теоремы

Слайд 5 Теорема Эйлера
Для любого выпуклого многогранника число вершин (В),

Теорема ЭйлераДля любого выпуклого многогранника число вершин (В), число рёбер (Р)

число рёбер (Р) и граней (Г) связаны формулой:
В+Г-Р= 2


Слайд 6 Задача 1
Выполняется ли
соотношение Эйлера для
невыпуклой призмы?
Ответ:

Задача 1Выполняется ли соотношение Эйлера для невыпуклой призмы?Ответ: Да.

Да.

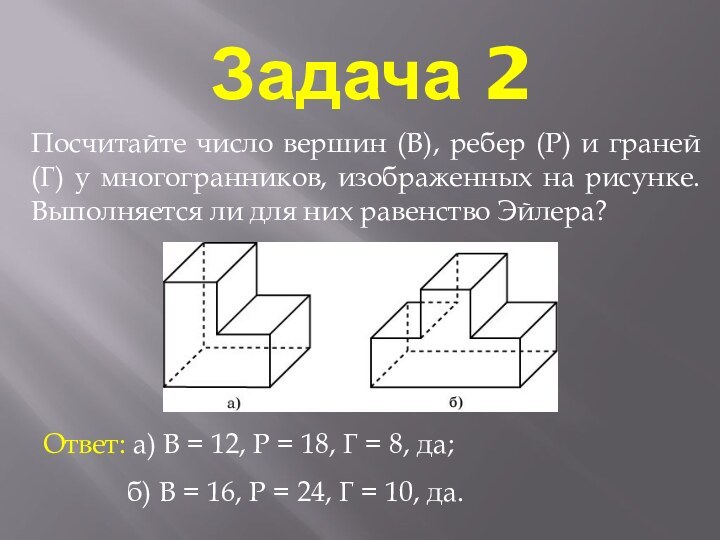
Слайд 7 Задача 2
Посчитайте число вершин (В), ребер (Р) и

Задача 2Посчитайте число вершин (В), ребер (Р) и граней (Г) у

граней (Г) у многогранников, изображенных на рисунке. Выполняется ли

для них равенство Эйлера?

Ответ: а) В = 12, Р = 18, Г = 8, да;

б) В = 16, Р = 24, Г = 10, да.

  • Имя файла: teorema-eylera.pptx
  • Количество просмотров: 124
  • Количество скачиваний: 0
- Предыдущая Свет как энергия
Следующая - Решение задач по геометрии

Похожие презентации

Атамекен ашық сабақ 8 сынып Атамекен ашық сабақ 8 сынып 256
Презентация сканворда по парикмахерскому искусству Презентация сканворда по парикмахерскому искусству 144
Влияние ГАДЖЕТОВ на развитие ребенка: плюсы и минусы консультация по теме Влияние ГАДЖЕТОВ на развитие ребенка: плюсы и минусы консультация по теме 173
Тема курсового проекта Тема курсового проекта 139
День молодых добровольцев России День молодых добровольцев России 140
Тактика игрового взаимодействия взрослого с детьми при руководстве режиссёрской игрой. презентация к занятию (подготовительная группа) Тактика игрового взаимодействия взрослого с детьми при руководстве режиссёрской игрой. презентация к занятию (подготовительная группа) 54
Презентация Зимняя сказка. Зрительная гимнастика Презентация Зимняя сказка. Зрительная гимнастика 153
Первые макеты кувшинов от студии Лебедева Первые макеты кувшинов от студии Лебедева 136
Актуальность работы Актуальность работы 129
Презентация Приобщение детей к истокам устного народного творчества презентация к уроку (средняя группа) по теме Презентация Приобщение детей к истокам устного народного творчества презентация к уроку (средняя группа) по теме 136
ОБЕСПЕЧЕНИЕ КАЧЕСТВА И КОЛИЧЕСТВА ТОВАРОВ ОБЕСПЕЧЕНИЕ КАЧЕСТВА И КОЛИЧЕСТВА ТОВАРОВ 183
Презентация по русскому языку на тему Презентация по русскому языку на тему 140
Моё портфолио по технологии за 6 класс Моё портфолио по технологии за 6 класс 168
Презентация қазақ тілінен тақырыбы: жеті қазына мен жеті ырыс (8 сынып) Презентация қазақ тілінен тақырыбы: жеті қазына мен жеті ырыс (8 сынып) 206
Работа с родителями в контексте ФГОС ДО презентация Работа с родителями в контексте ФГОС ДО презентация 166
Дополнительная перфорация скважин Дополнительная перфорация скважин 173
Статистика в микробиологических исследованиях. Статистика в микробиологических исследованиях. 124
Презентация по экономике на тему Что такое есть работа Презентация по экономике на тему Что такое есть работа 133
Презентация Советы родителям будущих первоклассников презентация к занятию (подготовительная группа) Презентация Советы родителям будущих первоклассников презентация к занятию (подготовительная группа) 140
Мої спостереження за природою. Мої спостереження за природою. 117
Йога голоса на уроках английского языка Йога голоса на уроках английского языка 162
Технология производства пива сорта Ячменный колос Крепкое с годовой мощностью 55 тыс. дал Технология производства пива сорта Ячменный колос Крепкое с годовой мощностью 55 тыс. дал 183
Тренируем внимание и память. презентация к уроку (1 класс) Тренируем внимание и память. презентация к уроку (1 класс) 168
Посадка семян цветов презентация к уроку (младшая группа) Посадка семян цветов презентация к уроку (младшая группа) 169
Презентация День Защитника Отечества подготовительная группа. презентация к уроку (подготовительная группа) Презентация День Защитника Отечества подготовительная группа. презентация к уроку (подготовительная группа) 218
Список препаратов: Список препаратов: 137
Презентация к рабочей программе второй младшей группы. презентация к уроку (младшая группа) Презентация к рабочей программе второй младшей группы. презентация к уроку (младшая группа) 136
Презентация Работа с детьми на экологической тропе материал (подготовительная группа) Презентация Работа с детьми на экологической тропе материал (подготовительная группа) 142
Презентация Оказание первой медицинской помощи при ожогах и порезах Презентация Оказание первой медицинской помощи при ожогах и порезах 199
ОЧІ – “ДЗЕРКАЛО ДУШІ” ОЧІ – “ДЗЕРКАЛО ДУШІ” 148