- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теория графов
Содержание
- 2. Элементы теории множествМножество состоит из элементов, если
- 3. Два множестваЕсли каждый элемент множества A является
- 4. четыре действия, проводимые над множествами1.Объединение. Так называется
- 5. Классификация графовГрафы делятся на два класса: ориентированные
- 6. Определение неориентированного графаНеориентированным графом G(X,U) называется пара
- 7. Определение инцидентности и смежностиЕсли в некотором графе
- 8. Степень вершиныКоличество ребер, инцидентных данной вершине x
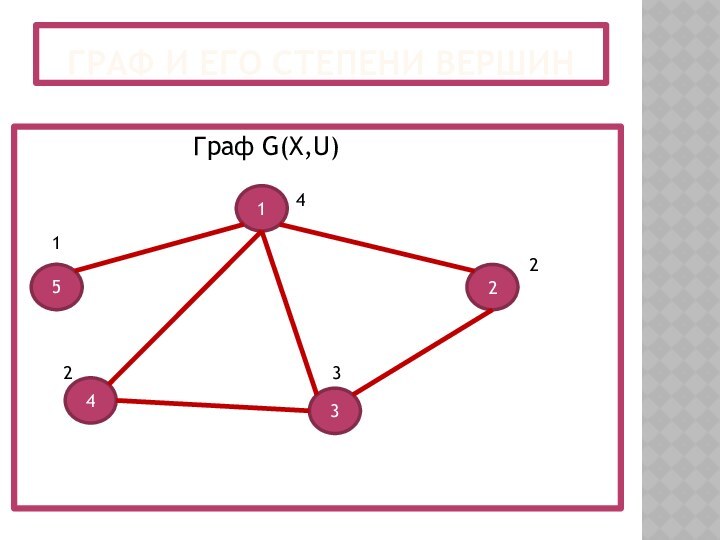
- 9. Граф и его степени вершин
- 10. Подграфы и суграфыПусть теперь
- 11. Матрица смежности вершинПрименительно к некоторому графу G(X,U)
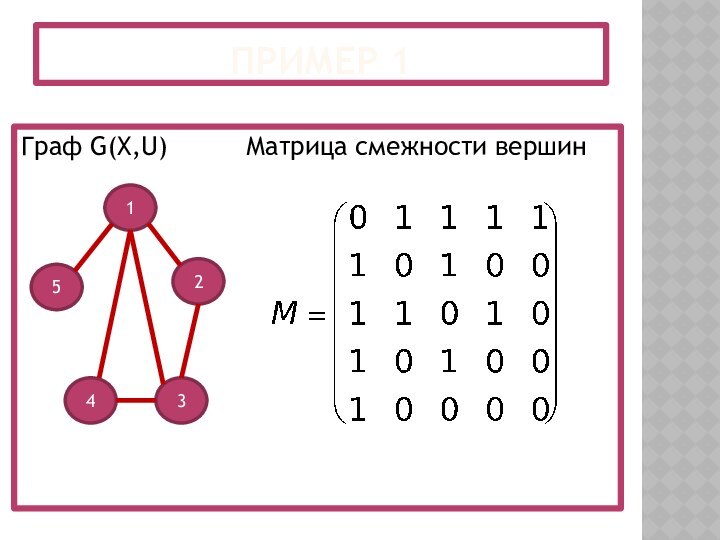
- 12. Пример 1Граф G(X,U) Матрица смежности вершин12345
- 13. Матрица инциденций графаПоставим в соответствие графу G(X,U)
- 14. Пример 2Граф G(X,U) Матрица инциденций12345
- 15. Маршруты на графах Маршрут в неориентированном
- 16. Связность графаВершины
- 17. Три операции на графах«Стягивание» ребра. Удаление вершины. Удаление ребра.
- 18. Деревья на графах Одним из важнейших
- 19. Эйлеровы циклыЭйлеровым циклом в графе называется цикл,
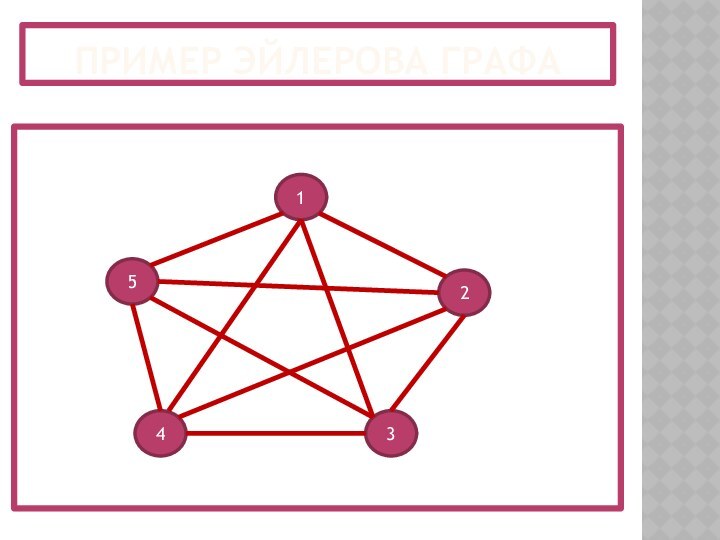
- 20. Пример Эйлерова графа 12345
- 21. Гамильтоновы графыГраф G(X,U) называется гамильтоновым, если в
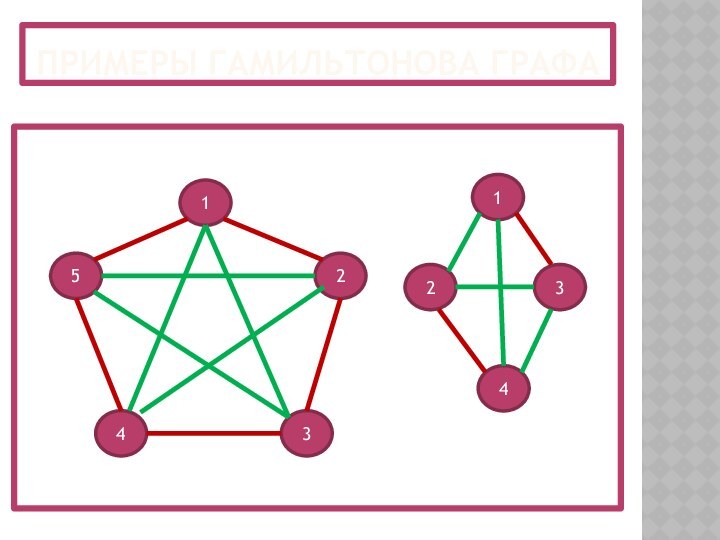
- 22. Примеры гамильтонова графа 123451234
- 23. Бихроматические графыГраф G(X,U) называется двудольным или бихроматическим
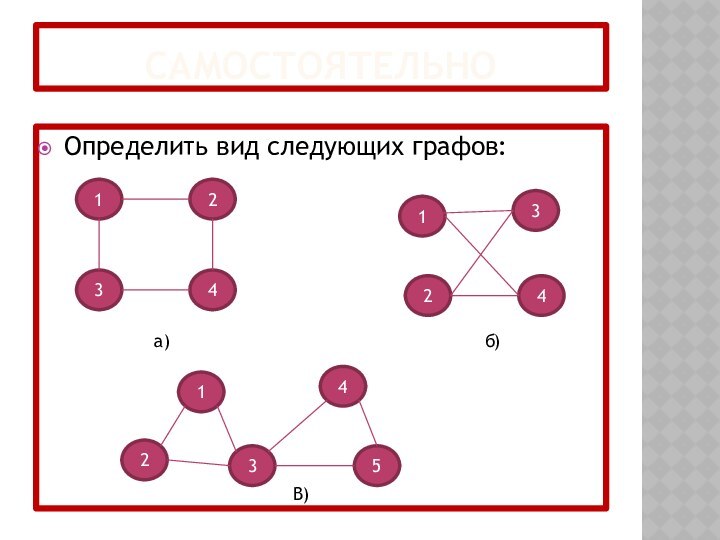
- 24. самостоятельноОпределить вид следующих графов:2413124354132В)
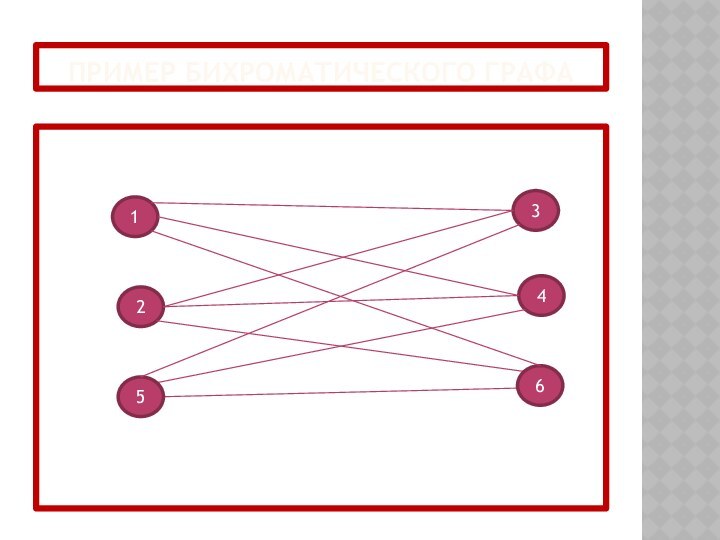
- 25. Пример бихроматического графа241356
- 26. Скачать презентацию
- 27. Похожие презентации
Элементы теории множествМножество состоит из элементов, если a является элементом множества A, то пишут , а если же a не является элементом множества A, то пишут . Символ




















Слайд 3
Два множества
Если каждый элемент множества A является элементом
множества B, то говорят, что A является подмножеством множества
B, что формально записывается следующим образом: . Пустое множество обозначается символом . Если одновременно и , то множества A и B называются равными: A = B.
Слайд 4
четыре действия, проводимые над множествами
1.Объединение. Так называется множество
C, которое строится по заданным множествам A и B
следующим образом: в него включаются все элементы из A и все элементы из B. Обозначение:2. Пересечение. Так называется множество C, которое строится по заданным множествам A и B следующим образом: в него включаются все элементы, принадлежащие одновременно множеству A и множеству B. Обозначение:
3. Вычитание. Так называется множество C, которое строится по заданным множествам A и B следующим образом: в него включаются все элементы из A, не принадлежащие множеству B. Обозначение:
4. Произведение. Так называется множество C, которое строится по заданным множествам A и B следующим образом: в него включаются все упорядоченные пары (a,b), где . Обозначение:
A
B
B
A
A
B
A
B
Слайд 5
Классификация графов
Графы делятся на два класса: ориентированные и
неориентированные. Применительно к последним обозначим через B множество всех
неупорядоченных пар различных элементов множества Х. Например, если Х={1,2,3}, то B={(1,2), (1,3), (2,3)}; если X={1,2}, то B={(1,2)}. Если X={1}, то , так как пар различных элементов в X нет. Применительно к неориентированным графам, когда в записи B={(1,2), (1,3), (2,3)} указывается пара (1,2), подразумевается, что выражения (1,2) и (2,1) означают одно и то же: это и означает, что пара неупорядочена, т.е. не имеет значения, в каком порядке записаны элементы пары.1
2
3
Слайд 6
Определение неориентированного графа
Неориентированным графом G(X,U) называется пара множеств
X, U, где X - любое непустое множество, а
U . Элементы множества Х называются вершинами графа, а элементы из U - его ребрами. Пример неориентированного графа G(X,U) приведен ниже на рисунке:5
4
3
2
1
Слайд 7
Определение инцидентности и смежности
Если в некотором графе G(X,U)
, где
пара вершин
такова, что , то вершины называются смежными; в этой ситуации каждая из них называется инцидентной ребру (i,j), а ребро (i,j) называется инцидентным каждой из вершин . 1
3
2
Слайд 8
Степень вершины
Количество ребер, инцидентных данной вершине x называется
ее степенью или локальной степенью графа в вершине x;
степень вершины x обозначается через d(x). В приведенном ниже рисунке степень вершины «1» равна 4, степень вершины «2» равна 2, степень вершины «3» равна 3, степень вершины «4» равна 2, степень вершины «5» равна 1. Вершины со степенью 0 называются изолированными. В любом графе количество вершин нечетной степени обязательно четно.
Слайд 10
Подграфы и суграфы
Пусть теперь
- два графа таких, что и ; тогда говорят, что является подграфом графа
. Если в некотором графе G(X,U) множество ребер B таково, что
то граф называется полным. Если графы и таковы, что и , то является суграфом графа .
Слайд 11
Матрица смежности вершин
Применительно к некоторому графу G(X,U) построим
квадратную матрицу М, такую, что:
Очевидно, эта матрица симметрична относительно
главной диагонали. Она называется матрицей смежности вершин графа G(X,U).
Слайд 13
Матрица инциденций графа
Поставим в соответствие графу G(X,U)
еще одну матрицу N, которую определим следующим образом:
Введенная таким
образом матрица N называется матрицей инциденций данного графа.
Слайд 15
Маршруты на графах
Маршрут в неориентированном графе
между вершинами и –
это последовательность вершин и ребер, обозначаемая символом видагде:
Если среди вершин и ребер маршрута отсутствуют повторы, то маршрут называется простым, в противном случае - сложным.
Слайд 16
Связность графа
Вершины в
приведенных выше обозначениях называются концами маршрута и связанными или
соединенными маршрутом L(1,n). Граф, в котором связанны любые две вершины, называется связным.Маршрут, в котором совпадают концевые вершины, называется циклом, а цикл, в котором нет повторяющихся вершин, кроме концевых, называется простым. Легко убедиться, что степени всех вершин связного графа G(X,U), состоящего из одного простого цикла, равны двум.
Слайд 18
Деревья на графах
Одним из важнейших видов
связных графов является дерево – это связный граф без
циклов. Применительно к любому графу G(X,U) такого рода справедливо:любые две вершины в дереве связаны единственным простым маршрутом.
Слайд 19
Эйлеровы циклы
Эйлеровым циклом в графе называется цикл, который
содержит все ребра и все вершины этого графа, причем
ребра в эйлеровом цикле не повторяются. Иными словами, при наличии эйлерова цикла в графе этот граф можно обойти по всем ребрам, пройдя каждое ребро только один раз. Граф, обладающий эйлеровым циклом, сам называется эйлеровым графом. Эйлеровы графы полностью описываются следующей теоремой, доказанной Эйлером:Теорема Эйлера: граф является эйлеровым тогда и только тогда, когда:
он связен,
все его локальные степени четны.
Слайд 21
Гамильтоновы графы
Граф G(X,U) называется гамильтоновым, если в нем
существует простой цикл, содержащий все вершины графа. Например, каждый
полный граф – гамильтонов, потому что в нем проведены всевозможные ребра и, в частности, те, благодаря которым возможен обход по всем вершинам. Общих и легко осуществляемых действий, с помощью которых можно было бы достоверно выяснить, является ли данный граф гамильтоновым, не существует, однако, имеются достаточные условия, которые легко проверяются. Например, если степень каждой вершины графа G(X,U) не меньше величины 0,5∙IXI, то граф G(X,U) является гамильтоновым (условие Дирака).
Слайд 23
Бихроматические графы
Граф G(X,U) называется двудольным или бихроматическим (см.
часть 1, главу 1.4), если его множество вершин X
можно представить в виде объединения двух его непустых подмножеств без общих элементов:,
так, что любое ребро множества U будет иметь один конец в одной из вершин подмножества , а другой конец - в одной из вершин подмножества





























