- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теория телетрафика в мультисервисных сетях. Потоки вызовов. Классификация моделей. (Лекция 2)
Содержание
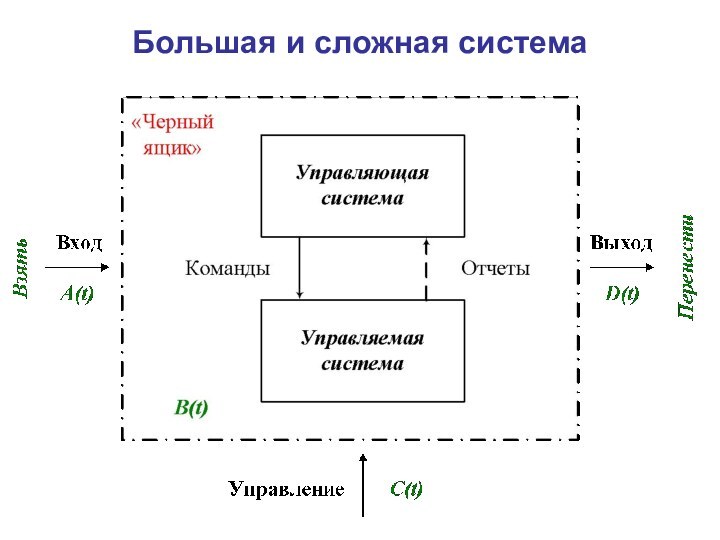
- 2. Большая и сложная система
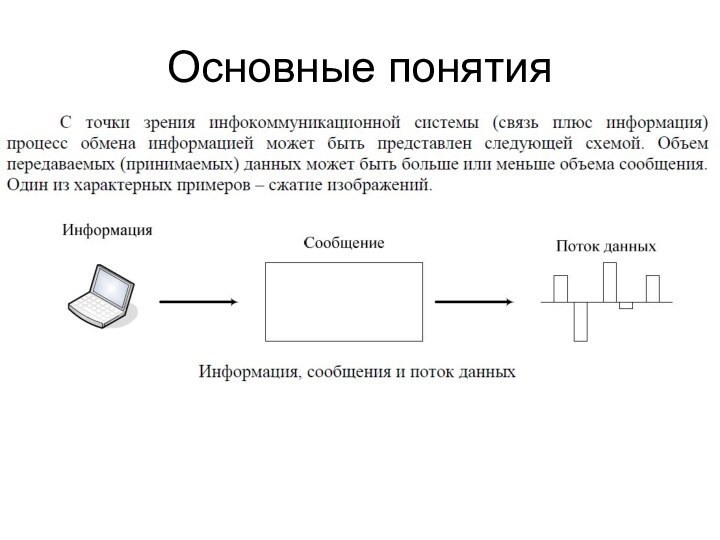
- 3. Основные понятия
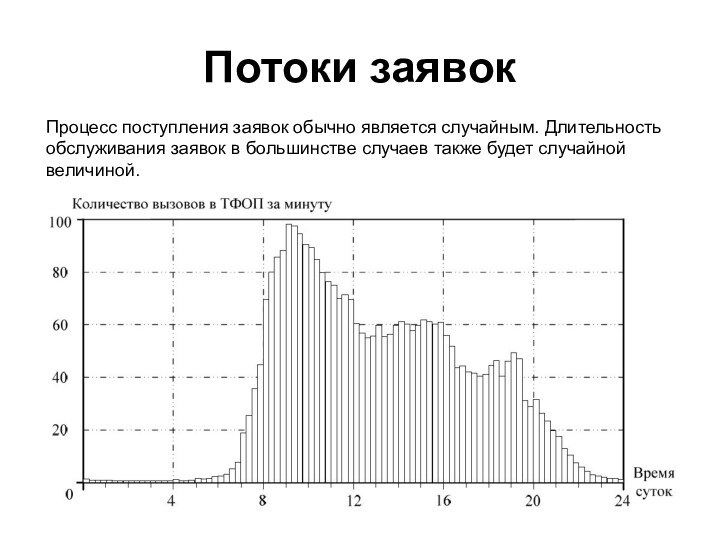
- 4. Потоки заявокПроцесс поступления заявок обычно является случайным.
- 5. Потоки заявок
- 6. Потоки заявокПоток заявок – последовательность поступления моментов
- 7. Потоки заявокПромежутки между вызовами: Zn=tn-tn-1Момент времени –
- 8. Способы задания потоков При помощи наступления моментов
- 9. Потоки заявок
- 10. Свойства потоковСтационарность.Поток называется стационарным, если вероятность поступления
- 11. Стационарность
- 12. Последействие.Свойства потоковПоток вызовов является потоком без последействия,
- 13. Последействие.
- 14. Свойства потоковОрдинарностьПоток вызовов называется ординарным, если вероятность
- 15. Свойства потоковПотоки вызововСлучайныеНеслучайныеСтационарностьПоследействиеОрдинарностьСтационарныеНестационарныеБез последействия С последействиемОрдинарныеНеординарные
- 16. Характеристики потоковВедущая функция потока - Λ[0;t) Интенсивность потока - λПараметр потока – П(t)
- 17. Ведущая функция потокаΛ[0;t) – это математическое ожидание
- 18. Интенсивность потокаМгновенная интенсивность потока - λ(t) -
- 19. Параметр потокаПараметр случайного потока вызовов - Π
- 20. Параметр потокаСтационарный потокВ отличие от ведущей функции
- 21. Простейший потокПростейший поток – это стационарный, ординарный
- 22. Простейший потокСреднее число заявок, поступающих за время
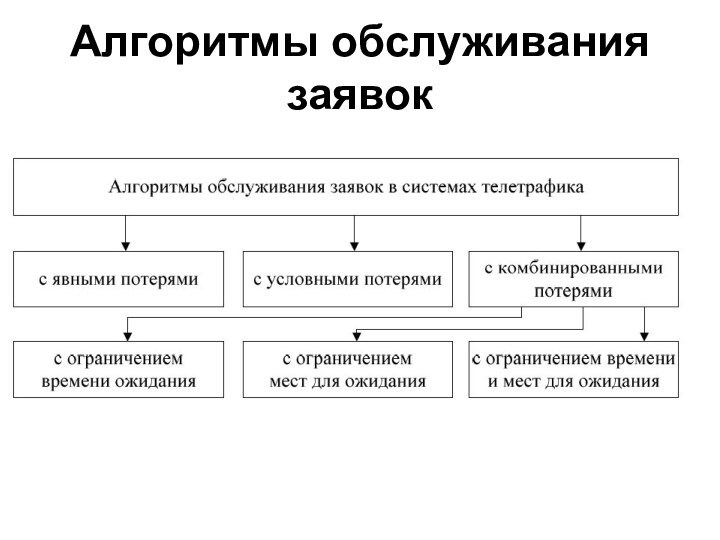
- 23. Алгоритмы обслуживания заявок
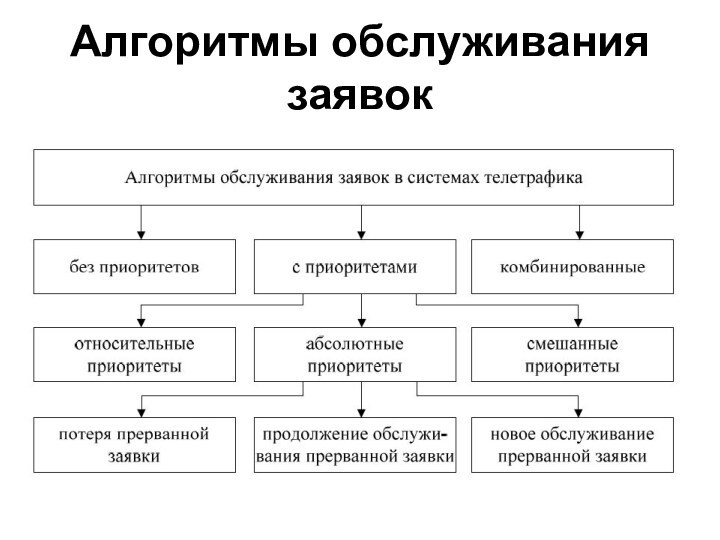
- 24. Алгоритмы обслуживания заявок
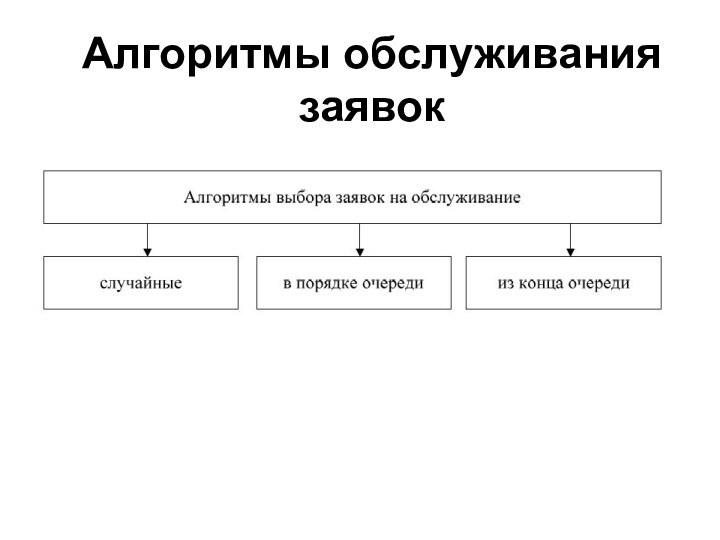
- 25. Алгоритмы обслуживания заявок
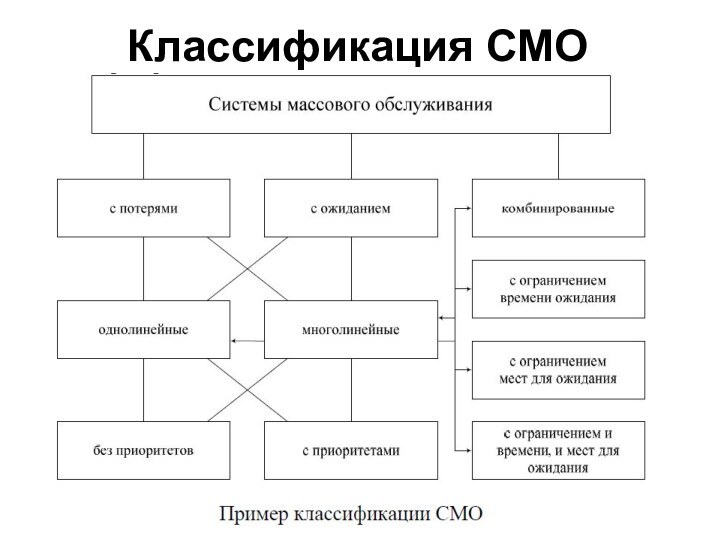
- 26. Классификация СМО
- 27. Классификация СМОA(x) | B(x) | v |
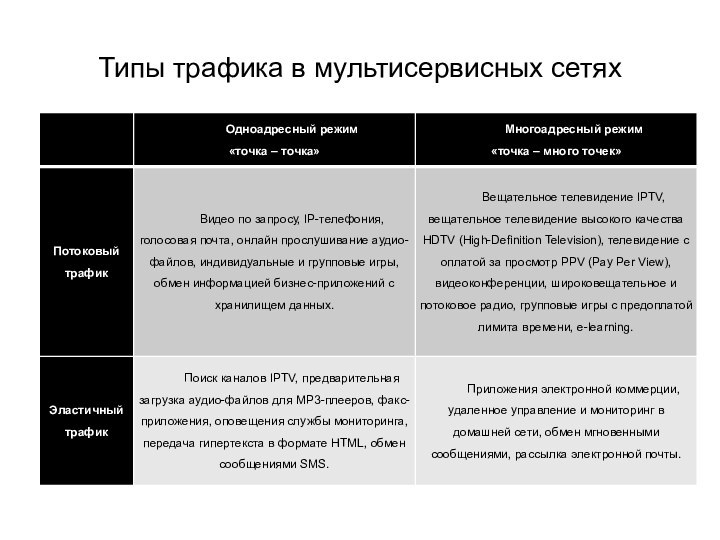
- 28. Типы трафика в мультисервисных сетях
- 29. Использованные источники Мышкис А.Д. Элементы теории математических
- 30. Скачать презентацию
- 31. Похожие презентации
















Слайд 4
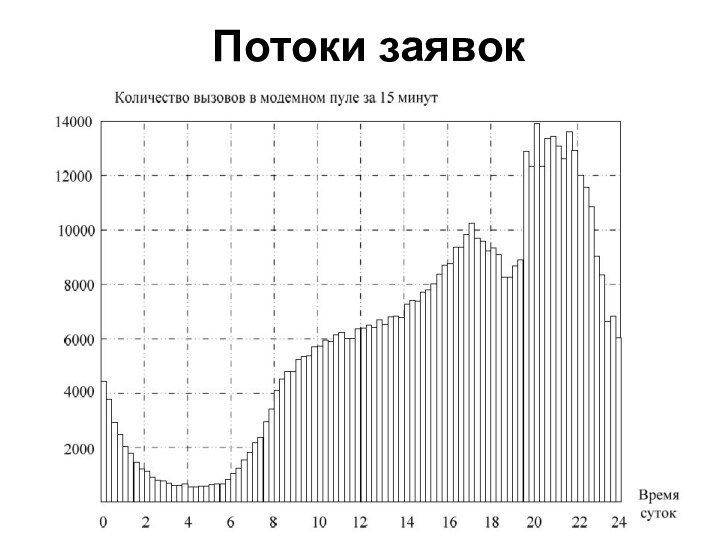
Потоки заявок
Процесс поступления заявок обычно является случайным. Длительность
обслуживания заявок в большинстве случаев также будет случайной величиной.
Слайд 6
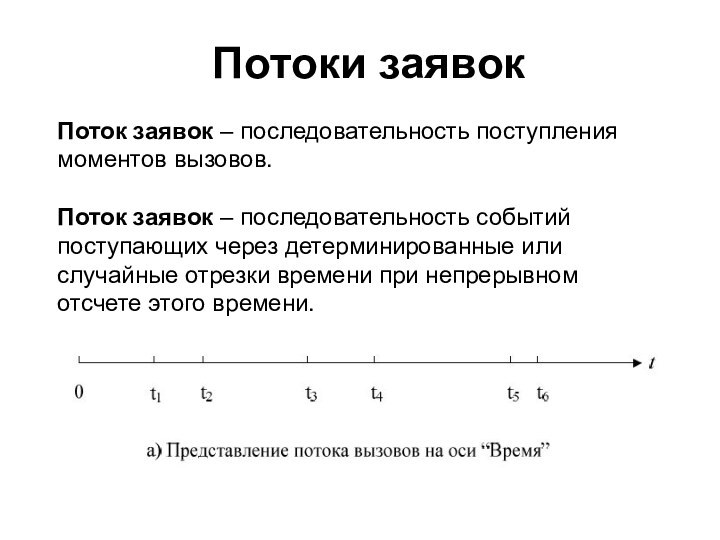
Потоки заявок
Поток заявок – последовательность поступления моментов вызовов.
Поток
заявок – последовательность событий поступающих через детерминированные или случайные
отрезки времени при непрерывном отсчете этого времени.
Слайд 7
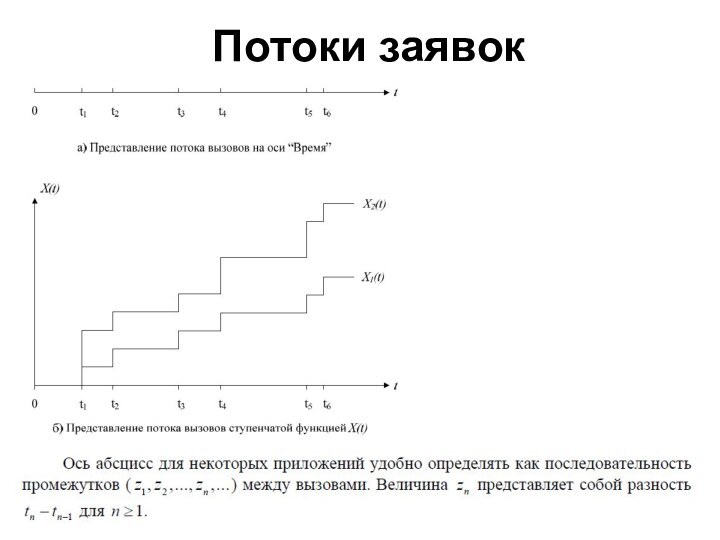
Потоки заявок
Промежутки между вызовами: Zn=tn-tn-1
Момент времени – число
соответствующее промежутку времени от начала отсчета до рассматриваемой точки
на оси времени.
Слайд 8
Способы задания потоков
При помощи наступления моментов вызовов:
t1
t2 t3 t4 ….. ti tj ……
При
помощи задания промежутков между вызовамиZ1 Z2 Z3 Z4 ….. Zn
3. При помощи чисел Ki: K – количество вызовов поступающих за промежуток [0; t1]; [0; t2]; [0; tn]
Все три способа задания потоков - эквивалентны
Слайд 10
Свойства потоков
Стационарность.
Поток называется стационарным, если вероятность поступления вызовов
случайного потока или число поступающих вызовов для детерминированного потока
за любой промежуток времени зависит только от длины промежутка и не зависит от того, где на оси времени этот промежуток расположен.
Слайд 12
Последействие.
Свойства потоков
Поток вызовов является потоком без последействия, если
вероятность поступления вызовов для случайного потока или число поступивших
вызовов для детерминированного потока за любой промежуток времени не зависит от количества , от времени поступления и окончания вызова, то есть не зависит от предыдущих событий.Таким образом для потока без последействия прошлая история не играет никакой роли для прогнозирования его будущего.
Слайд 14
Свойства потоков
Ординарность
Поток вызовов называется ординарным, если вероятность поступления
2 и более вызовов на бесконечно-малом отрезке времени ԏ
есть величина более высоко порядка, чем ԏ.Практически ординарность потока означает невозможность поступления 2 и более вызовов в любой момент времени.
Слайд 15
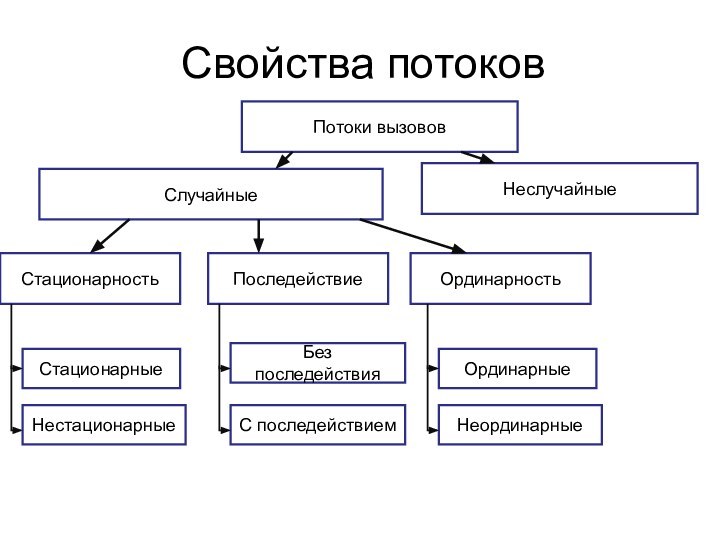
Свойства потоков
Потоки вызовов
Случайные
Неслучайные
Стационарность
Последействие
Ординарность
Стационарные
Нестационарные
Без последействия
С последействием
Ординарные
Неординарные
Слайд 16
Характеристики потоков
Ведущая функция потока - Λ[0;t)
Интенсивность потока
- λ
Параметр потока – П(t)
Слайд 17
Ведущая функция потока
Λ[0;t) – это математическое ожидание числа
вызовов в интервале времени [0;t).
Λ[0;t) – не отрицательная,
не убывающая и в практических задачах принимает конечное значение.
Слайд 18
Интенсивность потока
Мгновенная интенсивность потока - λ(t) - математическое
ожидание числа вызовов, поступающих в единицу времени.
Нестационарный поток
, если
такой предел существуетСтационарный поток
λ – конечное значение математическое ожидание числа вызовов, поступающих в единицу времени.
Размерность: 1/t
Λ[0;t) = λ*t , из-за свойства аддитивности
Слайд 19
Параметр потока
Параметр случайного потока вызовов - Π (t)
– в момент времени t - это предел отношения
вероятности поступления одного и более вызовов на отрезке времени [t;t+ԏ].Параметр случайного потока вызовов определяет в момент времени – плотность вероятности наступления вызывающего момента.
Практически параметр случайного потока вызовов характеризует частоту наступления вызывающих моментов.
Слайд 20
Параметр потока
Стационарный поток
В отличие от ведущей функции потока
параметр потока характеризует не поток вызовов, а поток вызывающих
моментов.Кроме того поток вызовов относится не ко всему отрезку времени, а только к фиксированному моменту времени.
Слайд 21
Простейший поток
Простейший поток – это стационарный, ординарный поток
без последействия
Описать поток удобно через функцию вероятности поступления K
вызовов PK(t)-?Распределение Пуассона
Функция распределения промежутков времени между вызовами
Экспоненциальное распределение
Слайд 22
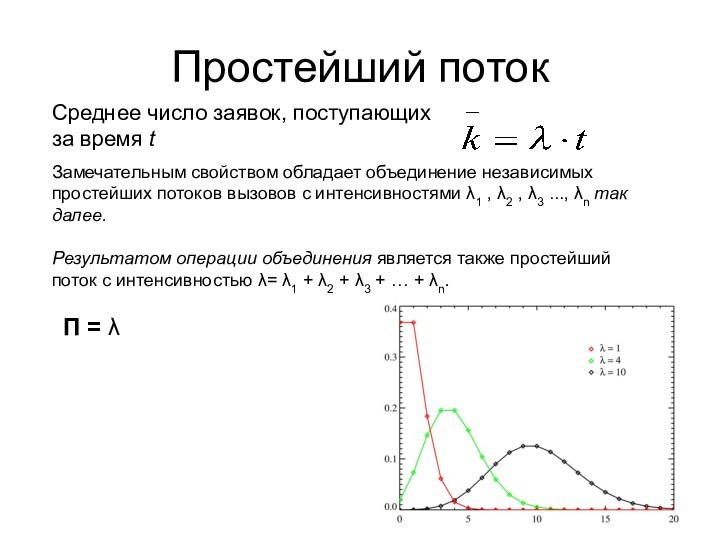
Простейший поток
Среднее число заявок, поступающих за время t
Замечательным
свойством обладает объединение независимых простейших потоков вызовов с интенсивностями
λ1 , λ2 , λ3 ..., λn так далее.Результатом операции объединения является также простейший поток с интенсивностью λ= λ1 + λ2 + λ3 + … + λn.
Π = λ
Слайд 27
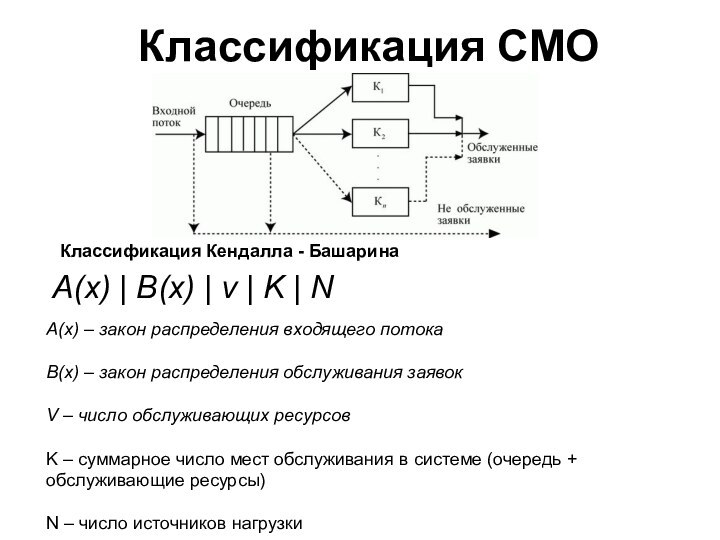
Классификация СМО
A(x) | B(x) | v | K
| N
Классификация Кендалла - Башарина
A(x) – закон распределения входящего
потокаB(x) – закон распределения обслуживания заявок
V – число обслуживающих ресурсов
K – суммарное число мест обслуживания в системе (очередь + обслуживающие ресурсы)
N – число источников нагрузки
Слайд 29
Использованные источники
Мышкис А.Д. Элементы теории математических моделей.
– М.: Книжный дом "Либриком", 2011.
Маликов Р.Ф. Основы
математического моделирования. – М.: Горячая линия – Телеком, 2010.Качала В.В. Основы теории систем и системного анализа. – М.: Горячая линия – Телеком, 2007.
Городецкий А.Е., Дубаренко В.В., Тарасова И.Л., Шереверов А.В. Программные средства интеллектуальных систем. – СПб.: Изд-во СПбГТУ, 2000.
Тарасенко Ф.П. Прикладной системный анализ. – М.: КНОРУС, 2010.
Кондаков Н.И. Логический словарь-справочник. – М.: Наука, 1976.
Энциклопедии и словари.
Ресурсы Internet.