Слайд 2
Трехфазные цепи – наиболее распространенные в современной электроэнергетике.
Это объясняется рядом их преимуществ по сравнению как с
однофазными, так и с другими многофазными цепями:
экономичность производства и передачи энергии по сравнению с однофазными цепями;
возможность сравнительно простого получения кругового вращающегося магнитного поля, необходимого для трехфазного асинхронного двигателя;
возможность получения в одной установке двух эксплуатационных напряжений – фазного и линейного
Слайд 3
Трехфазная цепь состоит из трех основных элементов: трехфазного
генератора, в котором механическая энергия преобразуется в электрическую с
трехфазной системой ЭДС; линии передачи со всем необходимым оборудованием; приемников (потребителей), которые могут быть как трехфазными (например, трехфазные асинхронные двигатели), так и однофазными (например, лампы накаливания).
Слайд 4
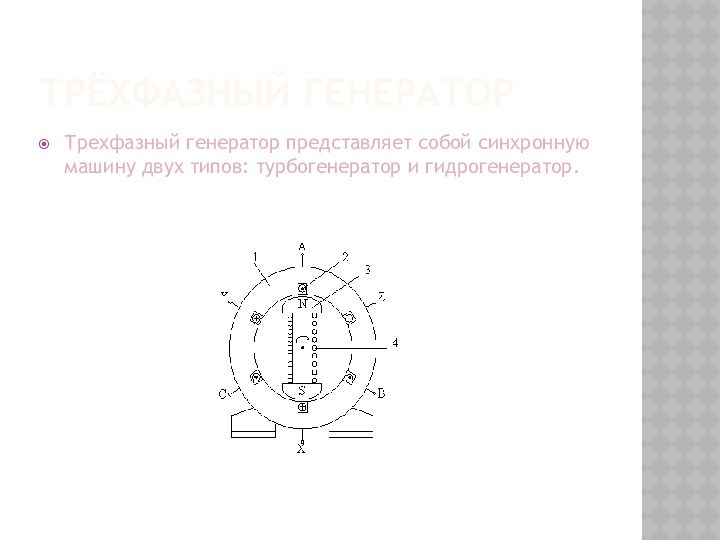
Трёхфазный генератор
Трехфазный генератор представляет собой синхронную машину двух
типов: турбогенератор и гидрогенератор.
Слайд 5
На статоре 1 генератора размещается обмотка 2, состоящая
из трех частей или, как их принято называть, фаз.
Обмотки фаз располагаются на статоре таким образом, чтобы их магнитные оси были сдвинуты в пространстве относительно друг друга на угол 2π/3, т.е. на 120°.Каждая фаза обмотки статора условно показана состоящей из одного витка. Начала фаз обозначены буквами A, B и C, а концы – X, Y, Z. Ротор 3 представляет собой электромагнит, возбуждаемый постоянным током обмотки возбуждения 4, расположенной на роторе.
Слайд 6
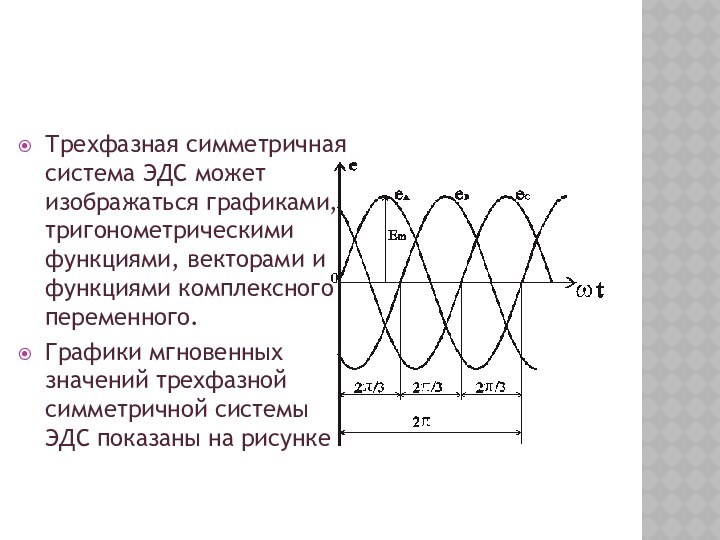
Трехфазная симметричная система ЭДС может изображаться графиками, тригонометрическими
функциями, векторами и функциями комплексного переменного.
Графики мгновенных значений трехфазной
симметричной системы ЭДС показаны на рисунке
Слайд 7
Если ЭДС одной фазы (например, фазы A) принять за
исходную и считать её начальную фазу равной нулю, то
выражения мгновенных значений ЭДС можно записать в виде
eA=Emsinωt,
eB=Emsin(ωt−120°),
eC=Emsin(ωt−240°)=Emsin(ωt+120°).
Комплексные действующие ЭДС будут иметь выражения:
ĖA=Emej0°=Em(1+j0),
ĖB=Eme−j120°=Em(−1/2−j/2),
ĖC=Eme+j120°=Em(−1/2+j/2).
Слайд 8
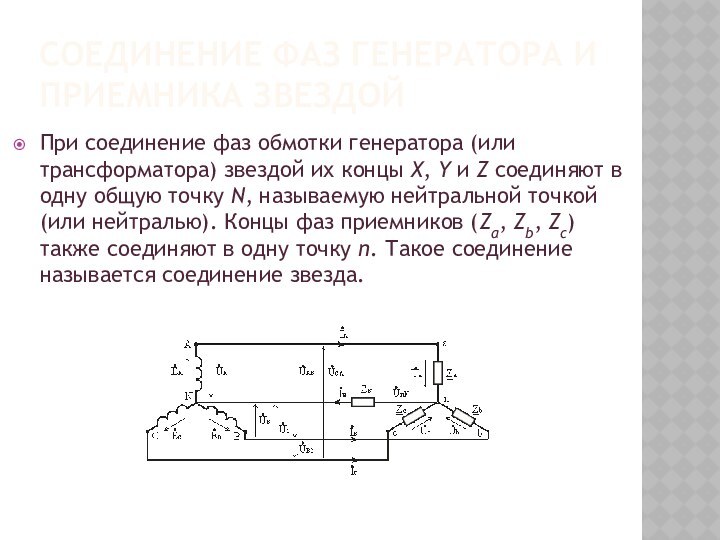
Соединение фаз генератора и приемника звездой
При соединение фаз
обмотки генератора (или трансформатора) звездой их концы X, Y и Z соединяют в одну
общую точку N, называемую нейтральной точкой (или нейтралью). Концы фаз приемников (Za, Zb, Zc) также соединяют в одну точку n. Такое соединение называется соединение звезда.
Слайд 9
Провода A−a, B−b и C−c, соединяющие начала фаз генератора и приемника, называются
линейными, провод N−n, соединяющий точку N генератора с точкой n приемника, – нейтральным.
Трехфазная цепь
с нейтральным проводом будет четырехпроводной, без нейтрального провода – трехпроводной.
В трехфазных цепях различают фазные и линейные напряжения. Фазное напряжение UФ – напряжение между началом и концом фазы или между линейным проводом и нейтралью (UA, UB, UC у источника; Ua, Ub, Uc у приемника). Если сопротивлением проводов можно пренебречь, то фазное напряжение в приемнике считают таким же, как и в источнике. (UA=Ua, UB=Ub, UC=Uc). За условно положительные направления фазных напряжений принимают направления от начала к концу фаз.
Слайд 10
Линейное напряжение (UЛ) – напряжение между линейными проводами
или между одноименными выводами разных фаз (UAB, UBC,UCA). Условно положительные
направления линейных напряжений приняты от точек, соответствующих первому индексу, к точкам соответствующим второму индексу (рис. 3.6).
По аналогии с фазными и линейными напряжениями различают также фазные и линейные токи:
Фазные (IФ) – это токи в фазах генератора и приемников.
Линейные (IЛ) – токи в линейных проводах.
При соединении в звезду фазные и линейные токи равны
IФ=IЛ.
Ток, протекающий в нейтральном проводе, обозначают IN.
По первому закону Кирхгофа для нейтральной точки n (N) имеем в комплексной форме
İN=İA+İB+İC
Слайд 11
Симметричная нагрузка приемника
При симметричной системе напряжений и симметричной
нагрузке, когда Za = Zb = Zc, т.е. когда Ra = Rb = Rc = Rф и Xa = Xb = Xc = Xф, фазные токи равны
по значению и углы сдвига фаз одинаковы
Ia = Ib = Ic = Iф = Uф / Zф,
φa = φb = φc = φ = arctg (Xф/Rф).
Слайд 12
Несимметричная нагрузка приемника
При симметричной системе напряжений и несимметричной
нагрузке, когда Za ≠ Zb ≠ Zc и φa ≠ φb ≠ φc токи в фазах потребителя различны и
определяются по закону Ома
İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc.
Ток в нейтральном проводе İN равен геометрической сумме фазных токов
İN = İa + İb + İc.
Напряжения будут Ua = UA; Ub = UB; Uc = UC, UФ = UЛ / , благодаря нейтральному проводу при ZN = 0.
Слайд 13
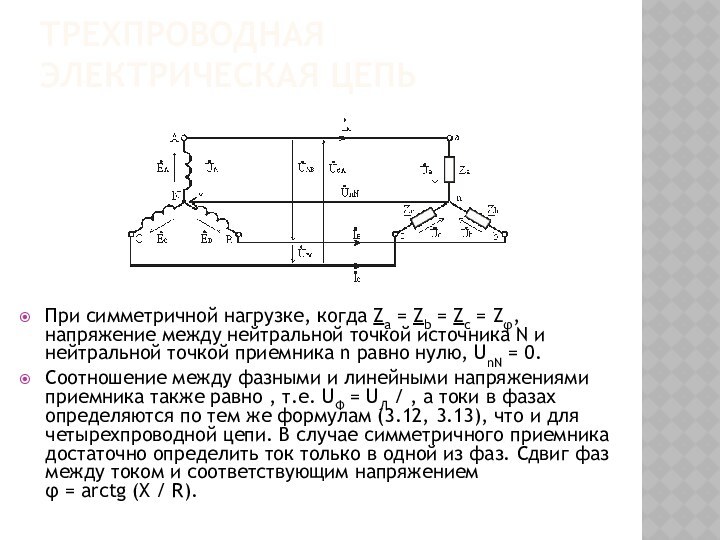
Трехпроводная электрическая цепь
При симметричной нагрузке, когда Za = Zb = Zc = Zφ, напряжение между
нейтральной точкой источника N и нейтральной точкой приемника n
равно нулю, UnN = 0.
Соотношение между фазными и линейными напряжениями приемника также равно , т.е. UФ = UЛ / , а токи в фазах определяются по тем же формулам (3.12, 3.13), что и для четырехпроводной цепи. В случае симметричного приемника достаточно определить ток только в одной из фаз. Сдвиг фаз между током и соответствующим напряжением φ = arctg (X / R).