Слайд 2
Искусство построения геометрических фигур при помощи циркуля и
линейки было в высокой степени развито в Древней Греции.
Евклид в своей книге "Начала" строго придерживается геометрических построений, выполняемых циркулем и линейкой, хотя названий инструментов он нигде не упоминает.
Однако древним ученым никак не удавалось выполнить некоторые построения, используя лишь циркуль и линейку, а построения, выполненные с помощью других инструментов, не считались геометрическими.
К числу таких задач относятся так называемые три знаменитые классические задачи древности:
Задача о квадратуре круга.
Задача о трисекции угла.
Задача об удвоении куба.
Слайд 3
Задача об удвоении куба
Считают, что задача об удвоении
куба появилась во времена пифагорейцев, около 540 г. до
н. э. Возможно, она возникла из задачи об удвоении квадрата, которую легко решить, опираясь на теорему Пифагора, — надо построить квадрат на диагонали данного квадрата. Согласно легенде, жители Афин, на которых боги ниспослали эпидемию чумы, отправили делегацию к оракулу на остров Делос за советом, как задобрить богов и избавиться от морового поветрия. Ответ был таков:
«Удвойте жертвенник храма Аполлона, и чума прекратится». Жертвенник имел кубическую форму. Афиняне решили, что задание простое, и построили новый жертвенник, с вдвое большим ребром. Однако чума только усилилась. Вторично обратились к оракулу и получили ответ: «Получше изучайте геометрию». История умалчивает о том, как удалось умилостивить богов, но чума в конце концов покинула город. А задачу об удвоении куба стали называть делосской задачей.
Слайд 4
Древние греки сравнительно легко решили задачу на удвоение
квадрата. Для этого надо было уметь строить при помощи
циркуля и линейки корень квадратный из двух. Действительно, если сторона данного квадрата равняется а, а сторона искомого квадрата - х, то согласно условию задачи будем иметь
х2 = 2 а2, откуда х = а .
Следовательно, в качестве х надо взять диагональ данного квадрата, которая по теореме Пифагора как раз и будет равняться.
Обобщая задачу об удвоении квадрата, древние греки перешли к рассмотрению задачи об удвоении куба и также стремились решить ее при помощи циркуля и линейки. Действительно, если ребро данного куба положить равным а, а ребро искомого куба - х, то согласно условию задачи будем иметь
х3 = 2 а3, откуда х = а .
Однако все старания построить циркулем и линейкой не увенчались успехом. Наконец, в первой половине XIX века было доказано, что при помощи одних только циркуля и линейки построить нельзя.
Слайд 5
Современными средствами доказано, что кубическое уравнение с рациональными
коэффициентами, не имеющее рациональных корней, не может быть разрешимо
- в квадратных радикалах, т. е. ни один из корней этого уравнения не может быть построен при помощи циркуля и линейки.
Выше было показано, что задача об удвоении куба сводится к решению кубического уравнения
х3 – 2а3 = 0,
где а – ребро данного куба, х - искомое ребро удвоенного куба.
Приняв для простоты длину ребра данного куба за 1, получим уравнение х3 – 2 = 0.. Это уравнение с рациональными коэффициентами, как легко убедиться, не может иметь рациональных корней. Следовательно, по предыдущей теореме задача об удвоении куба не может быть решена при помощи циркуля и линейки.
Слайд 6
Первым из ученых, кто открыто высказал мнение, что
точное построение отрезка, равного , посредством циркуля и линейки
неосуществимо, был знаменитый французский ученый Рено Декарт.
Строгое доказательство неразрешимости задачи об удвоении куба при помощи циркуля и линейки было дано французским математиком П. Венцелем в 1837 году.
Слайд 7
Но, еще Гиппократ Хиосский, знаменитый геометр V в.
до н. э., свёл удвоение куба к построению «двух
средних пропорциональных» х и у для данных отрезков а и b, т. е. к решению уравнений
a : x =x : y = y : b
(при b=2a получаем x=a). Эту идею удалось реализовать Платону около 340 г. до н. э. с помощью нетрадиционных чертёжных инструментов — двух прямых углов (рис. 1).
Слайд 8
Задача о трисекции угла
Требуется произвольный угол разделить на
три равные части. Выполнить построение способом Архимеда при помощи
циркуля и передвижной линейки с двумя отметками.
Происхождение задачи о трисекции угла связано с практической деятельностью, в частности, уметь делить окружность на равные части нужно было при изготовлении колеса со спицами, деление угла или дуги окружности на несколько равных частей необходимо было и в архитектуре, в создании орнаментов, в строительной технике и в астрономии.
Слайд 9
Простое решение задачи о трисекции угла при помощи
циркуля и подвижной линейки с двумя отметками дал Архимед.
На данный угол — это угол AОВ между радиусами окружности. С помощью меченой линейки проведём прямую через точку А так, чтобы её отрезок РQ между окружностью и продолжением прямой ВО равнялся радиусу окружности. Как и на рис. 3, здесь образуются равнобедренные треугольники ОАР и ОРQ, и легко доказать, что угол ОQA втрое меньше данного.
Слайд 10
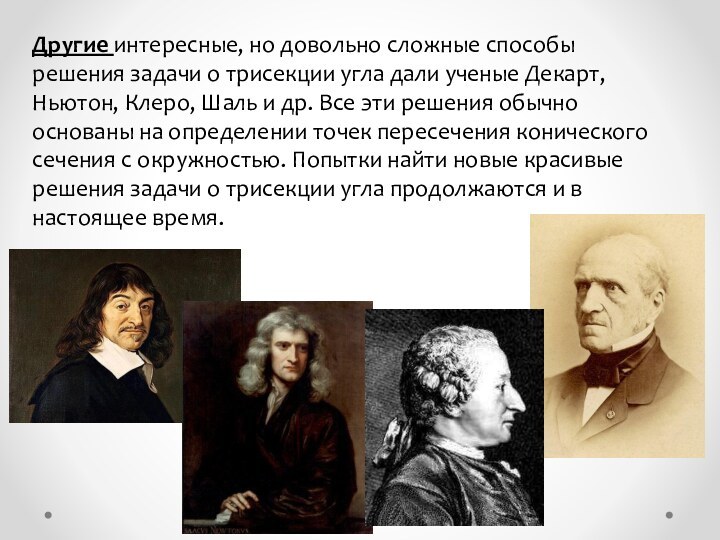
Другие интересные, но довольно сложные способы решения задачи
о трисекции угла дали ученые Декарт, Ньютон, Клеро, Шаль
и др. Все эти решения обычно основаны на определении точек пересечения конического сечения с окружностью. Попытки найти новые красивые решения задачи о трисекции угла продолжаются и в настоящее время.
Слайд 11
Задача о квадратуре круга
В задаче о квадратуре круга
требуется построить циркулем и линейкой квадрат, равновеликий данному кругу.
Вероятно,
задача была известна уже за две тысячи лет до н. э. в Древнем Египте и Вавилоне. Но первая прямая ссылка на неё относится к V в. до н. э. По свидетельству древнегреческого историка Плутарха, философ Анаксагор, коротая время в тюрьме, пытался квадрировать круг, т. е. превратить его в равновеликий квадрат. Если считать радиус данного круга равным 1, то сторона искомого квадрата должна составить .
Слайд 12
Надежды «квадратурщиков» подогревались существованием криволинейных фигур, квадрируемых циркулем
и линейкой. Гиппократ Хиосский нашёл одну из таких фигур,
известную как «луночки Гиппократа» (рис. 6). Он нашёл и другие луночки, допускающие квадратуру, что, конечно, не помогло ему решить саму исходную задачу. Заметим, что вопрос о том, какие луночки квадрируемы, оказался сложным и был полностью решён только в XX в., советским математиком Н. Г. Чеботарёвым.
Слайд 13
Было предложено множество построений. В лучшем случае они
давали приближённое значение p с достаточно хорошей точностью (см.,
например, рис. 7). Однако, в отличие от приведённых выше решений двух других знаменитых задач, эти построения были принципиально приближёнными. Впрочем, авторы таких построений часто не сомневались в их абсолютной точности и горячо отстаивали свои заблуждения. Один из самых громких споров на эту тему произошёл в Англии между двумя выдающимися учёными XVII в. — философом Томасом Гоббсом и математиком Джоном Валлисом. В весьма почтенном возрасте Гоббс опубликовал около десяти «решений» задачи о квадратуре круга.
Слайд 14
Итак, задача о квадратуре круга оказалась наиболее сложной
из трёх. Метод, использованный в двух других задачах, здесь
не подошёл, так как число p имеет совершенно другую природу, чем или корни уравнений, к которым сводится трисекция.
Только в 1882 г. Фердинанд Линдеман доказал, что число p трансцендентно, т. е. не является корнем никакого многочлена с целыми коэффициентами. Значит, оно и не квадратично-иррационально, поскольку в противном случае было бы корнем какого-либо многочлена. Так Линдеман наконец поставил точку в проблеме разрешимости посредством циркуля и линейки последней из трёх классических задач древности.