- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Управление запасами и их расчеты
Содержание
- 2. Определение оптимального размера заказа
- 4. Формула оптимального размера заказа для единственного продукта
- 6. Продифференцировав обе части уравнения и приравняв выражение к нулю, получим:
- 7. В результате получим:
- 8. Решим относительно Q:
- 10. Однопродуктовая статическая модель с разрывами цен
- 11. В предыдущей модели не учитывались удельные затраты
- 12. В таких случаях цена меняется скачкообразно или
- 13. Рассмотрим модель управления запасами с мгновенным пополнением
- 14. Тогда суммарные затраты на цикл помимо издержек оформления заказа и хранения запаса должен включать издержки приобретения.
- 15. Суммарные затраты на единицу времени при y
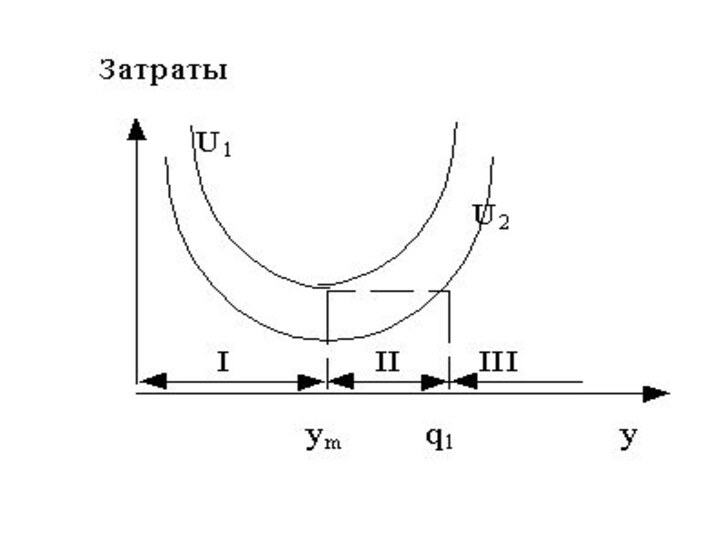
- 16. Пренебрегая влиянием снижения цен, обозначим через ym размер заказа, при котором достигается минимум U1(y)и U2(y).
- 18. Из вида функций затрат U1(y)и U2(y) следует,
- 19. Так как значение ym известно ( ), то решение
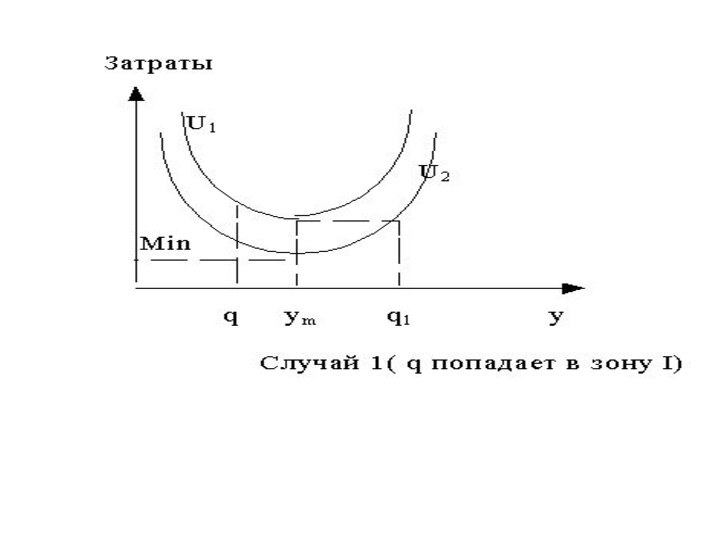
- 20. Алгоритм определения у* можно представить в следующем виде: 1. Определить . Если q
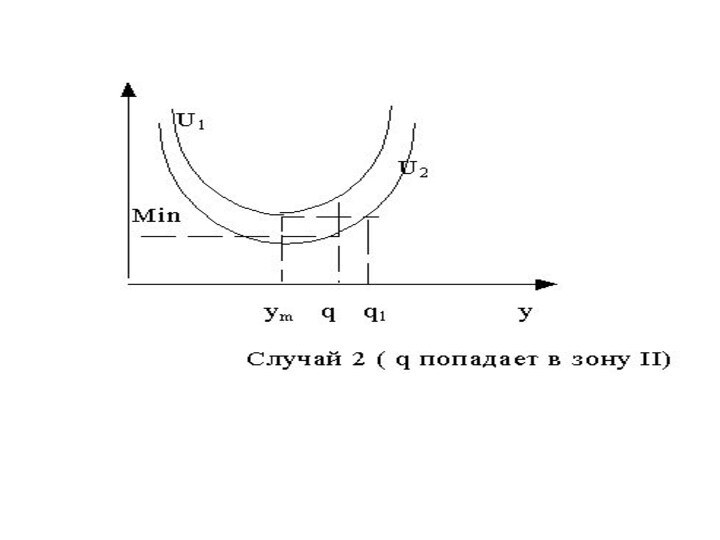
- 21. 2. Определить q1 из уравнения U1(ym) = U2(q1) и установить, где по отношению к зонам II и III находится значение q. а) если ym
- 25. Многопродуктовая статическая модель с ограничениями на емкость складских помещений.
- 26. Эта модель предназначена для системы управления запасами,
- 27. Пусть: А - максимально допустимая площадь складского
- 28. Ограничения на потребность в складском помещении принимают вид
- 29. Допустим, что запас продукции каждого вида пополняется
- 30. Пусть: - интенсивность спроса i-го вида продукции,
- 31. Общие затраты будут теми же, что и
- 32. Скачать презентацию
- 33. Похожие презентации
Определение оптимального размера заказа




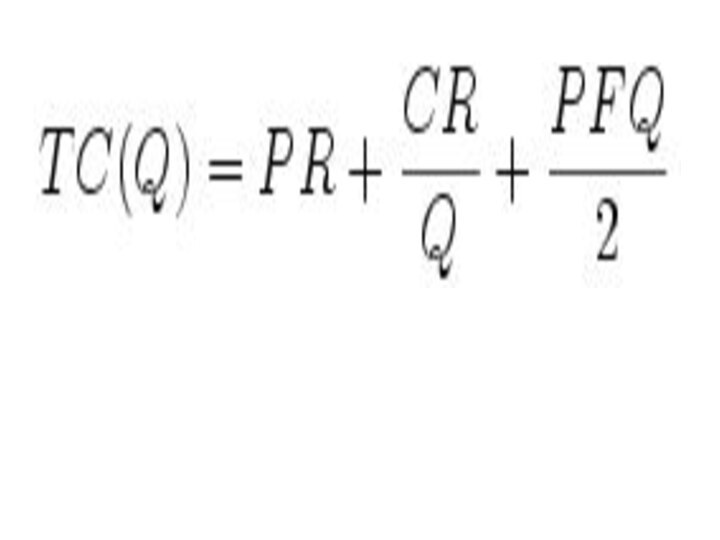



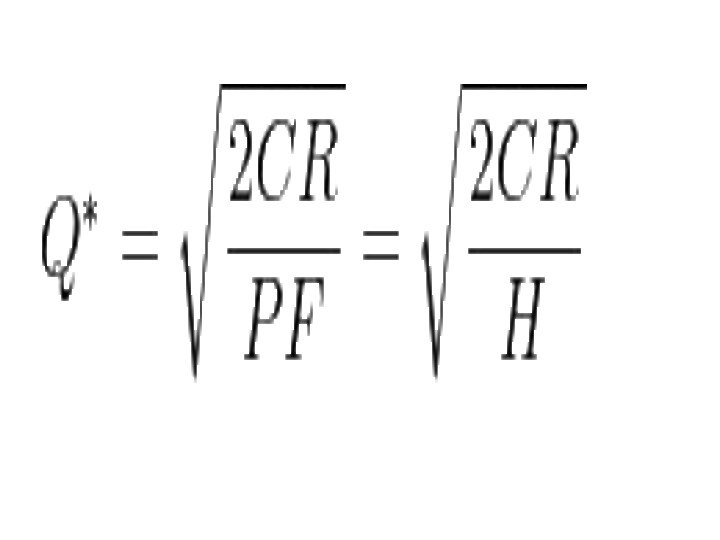




















Слайд 11 В предыдущей модели не учитывались удельные затраты на
приобретение товаров, т.к. они постоянны и не влияют на
уровень запаса. Однако нередко цена единицы продукции зависит от размеров закупаемой партии.Слайд 12 В таких случаях цена меняется скачкообразно или предоставляются
оптовые скидки. При этом в модели управления запасами необходимо
учитывать затраты на приобретение.Слайд 13 Рассмотрим модель управления запасами с мгновенным пополнением запаса
при отсутствии дефицита. Предположим, что цена единицы продукции равна
с1 при y=q, где с1 > с2 и q- размер заказа, при превышении которого предоставляется скидка.