- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему векторное исмешанное произведение векторов
Содержание
- 2. Правая и левая тройка векторовОТВЕТ: ПРАВАЯ тройка.ПРАВАЯ ТРОЙКАЛЕВАЯ ТРОЙКА
- 3. ВЕКТОРНОЕ произведение векторовОбозначение векторного произведения :
- 4. ЗАДАНИЕ: Второе и третье равенство проверить дома.
- 5. Свойства векторного произведения3. При перестановке множителей векторное
- 6. Геометрический смысл векторного произведенияТак как площадь треугольника равна ПОЛОВИНЕ площади параллелограмма, то
- 7. Критерий коллинеарности
- 8. Выражение векторного произведения через координатыДля запоминания этой
- 9. СМЕШАННОЕ (ВЕКТОРНО -СКАЛЯРНОЕ)произведение векторовСмешанное произведение НЕ
- 10. Геометрический смысл СМЕШАННОГО произведения
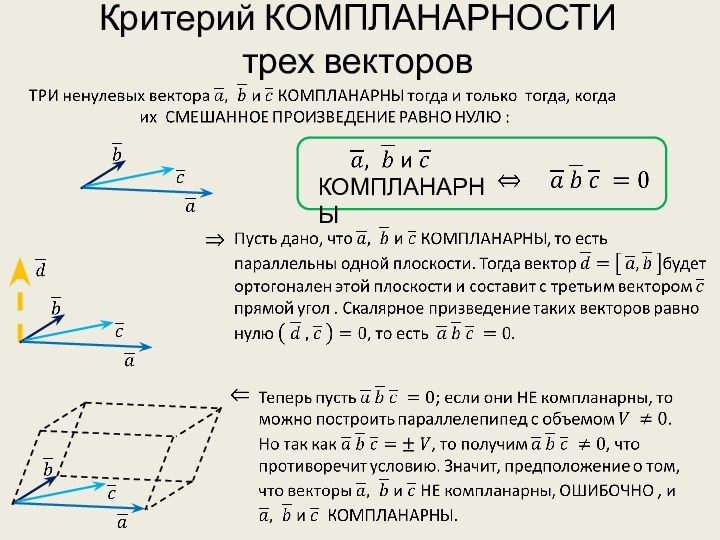
- 11. Критерий КОМПЛАНАРНОСТИ трех векторовКОМПЛАНАРНЫ
- 12. Выражение смешанного произведения через координатыЕсли найти их
- 13. Приложения смешанного произведенияВычисление объема треугольной пирамиды (тетраэдра)ВОПРОС:
- 14. Задача № 1РЕШЕНИЕ:По геометрическому смыслу векторного произведения:Вычисляем:
- 15. Задача № 2РЕШЕНИЕ:По геометрическому смыслу векторного произведения:По другой формуле:Из задачи 1 известно:ОТВЕТ: 5.
- 16. Задача № 3Проверить компланарность векторов:РЕШЕНИЕ:
- 17. Скачать презентацию
- 18. Похожие презентации
Правая и левая тройка векторовОТВЕТ: ПРАВАЯ тройка.ПРАВАЯ ТРОЙКАЛЕВАЯ ТРОЙКА
Слайд 5
Свойства векторного произведения
3. При перестановке множителей векторное произведение
МЕНЯЕТ ЗНАК на противоположный :
1. Постоянное число можно вносить и выносить за скобки
векторного произведения :
2. При векторном умножении суммы векторов на вектор можно раскрыть скобки :
Слайд 6
Геометрический смысл векторного произведения
Так как площадь треугольника равна
ПОЛОВИНЕ площади параллелограмма, то
Слайд 8
Выражение векторного произведения через координаты
Для запоминания этой формулы
удобно использовать символ ОПРЕДЕЛИТЕЛЯ третьего порядка:
Используя разложение определителя
по
элементам ПЕРВОЙ строки, получим:
Слайд 9
СМЕШАННОЕ
(ВЕКТОРНО -СКАЛЯРНОЕ)произведение векторов
Смешанное произведение НЕ МЕНЯЕТСЯ
при
перемене мест знаков
векторного и скалярного умножения :
ВОПРОС:
Смешанное произведение является ВЕКТОРОМ ИЛИ ЧИСЛОМ ? Смешанное произведение является ЧИСЛОМ.
Слайд 12
Выражение смешанного произведения через координаты
Если найти их смешанное
произведение, используя выражения в координатах для векторного и скалярного
произведений, то получим формулу:Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из КООРДИНАТ умножаемых векторов.
Слайд 13
Приложения смешанного произведения
Вычисление объема треугольной пирамиды (тетраэдра)
ВОПРОС: Зачем
нужен знак модуля у смешанного произведения?
ОТВЕТ: Смешанное произведение левой
тройки векторов - число отрицательное, а объем тела (пирамиды) не может быть меньше нуля, поэтому требуется знак модуля.
Слайд 15
Задача № 2
РЕШЕНИЕ:
По геометрическому смыслу векторного произведения:
По другой
