Слайд 2
Цикл с постусловием
При разработке программ очень удобно бывает
использовать цикл с постусловием (рис. 6.2 (б) ). Синтаксис
цикла с посту условием выглядит следующим образом:
Repeat
<Оператор 1>;
<Оператор 2>;
…
<Оператор N>;
Until <Условие>;
ело цикла.
Слайд 3
В операторе цикла с постусловием выражение, которое управляет
по-вторным выполнением последовательности операторов тела цикла (условие), содержится после
служебного слова Until. Между служебными словами Repeat и Until заключаются операторы, входящие в тело цикла.
Правила использования данного цикла, аналогично правилам цикла с While. Однако, прежде чем будет проверено условие выполнения тела цикла, правила использования данного цикла, аналогично правилам цикла с While. Однако, прежде чем будет проверено условие выполнения тела цикла
Слайд 5
Program Example_6_3;
Uses Crt; {подключаем модуль}
Var
{описываем переменные}
N: Integer;
S: Real;
Begin {Начало программы}
ClrScr; {очищаем экран}
S:=0; {задаем начальное значение}
N:=1; {задаем начальное значение}
Слайд 9
Repeat
S:=S+1/N; {Тело цикла}
N:=N+1
{Увеличиваем значение}
Until N>50; {Проверка на условие}
WriteLn ('Результат
суммирования...',S); {Вывод сообщение и результат}
End. {Конец программы}
Слайд 10
Итерационные циклы
Циклический процесс называется итерационным, если каждое новое
значение переменной цикла определятся через её предыдущее значение, число
повторяющихся вычислений в цикле неизвестно и определить заранее (без реализации программы) его невозможно, если выход из цикла осуществляется по достижению решением заданной точности.
Слайд 11
Другими словами, итерационный процесс имеет место в том
случае, если невозможно предсказать заранее через которое количество шагов
он закончится.
Итерационные циклы, реализующие метод последовательных приближений, широко используются в задачах с числовыми, функциональными и степенными рядами, при вычислении определённых интегралов, значений функций, в решении нелинейных алгебраических и трансцендентных (решающихся только графическим способом) уравнений.
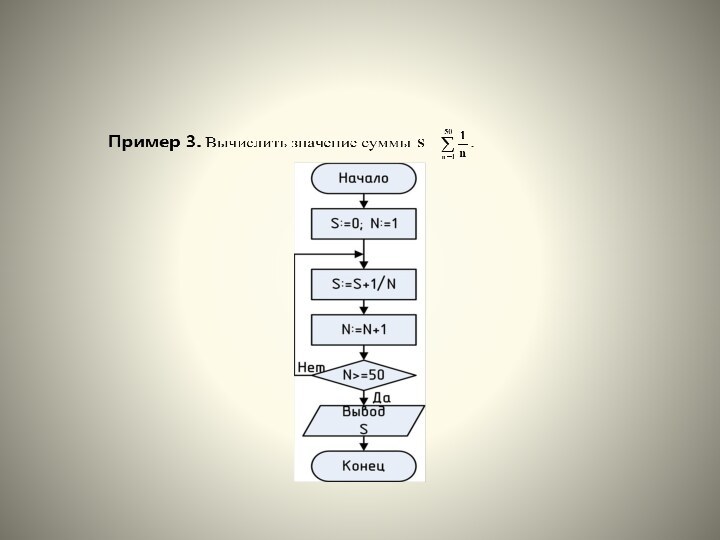
Слайд 12
Пример 4. Вычислить значение квадратного корня , по
итерационной формуле Ньютона
где i:={0,1,2,…}, а y(i+1) и y(i)
– два последовательных приближения к искомому корню. Начальные приближения корня вводится с клавиатуры.
Итерационный процесс для x>1 введется до тех пор, пока относительная погрешность при нахождения очередного приближения по абсолютному значению не станет меньше заданного значения h.
Слайд 13
Program Example_6_4; {Задача решена с пред-условием}
Uses Crt; {Подключаем модуль}
Var
x,y,h,y0,y1,y2:Real;
{Описываем переменные}
Begin {Начало программы}
ClrScr;
{Очищаем экран}
Слайд 14
Write ('Введите число, из которого необходимо извлечь корень
x=');
ReadLn (x); {Вводим с клавиатуры значение}
Write ('Введите начальное приближение
y=');
ReadLn (y0); {Вводим с клавиатуры значение}
Write ('Введите точность значения');
ReadLn (h); {Вводим с клавиатуры значение}
y:=y0; {Задаем начальное приближение}
While Abs(y1-y)>=h Do {Начало итерационного цикла}
Слайд 15
Begin
y2:=y+1/2*(x/y-y); {Вычисление очередного приближения}
y1:=y; y:=y2; {Переназначения}
End; {Конец итерационного цикла}
WriteLn ('значение корня равно',y); {Вывод
на экран значения корня}
End. {Конец программы}
Слайд 17
Program Example_6_5 { Задача решена с постусловием}
Uses Crt;
{Подключаем модуль}
Var
x,y,h,y0,y1,y2:Real; {Описываем переменные}
Begin {Начало
программы}
ClrScr; {Очищаем экран}
Write ('Введите число, из которого необходимо извлечь ко-рень x=');
ReadLn (x); {Вводим с клавиатуры значение}
Write ('Введите начальное приближение y=');
Слайд 18
ReadLn (y0); {Вводим с клавиатуры значение}
Write ('Введите точность
значения');
ReadLn (h); {Вводим с клавиатуры значение}
y:=y0; {Задаем начальное приближе-ние}
Repeat
{Начало итерационного цикла}
y2:=y+1/2*(x/y-y); {Вычисление очередного при-ближения}
y1:=y; y:=y2; {Переназначения}
Until Abs(y1-y)<=h;{Конец итерационного цикла}
WriteLn ('значение корня равно',y); {Вывод на экран значения корня}
End. {Конец программы}
Слайд 19
Лабораторная работа №4: Вложенные циклы
Цель работы: изучить принципы
проектирования и получить навыки в написании программ для задач
с вложенными циклами.
Слайд 20
Общие сведения
На практике часто встречаются задачи, в которых
число переменных, являющихся параметрами цикла, две и более. В
таких случаях алгоритм и программа предполагают несколько циклов, вложенных один в другой. Следовательно, вложенным называют любой цикл, содержащий внутри себя один или несколько других циклов (т.е. их схема напоминает “матрёшку”).
Слайд 21
Цикл, охватывающий другие называется внешним, а остальные по
отношению к нему - внутренние. Глубина вложений на практике
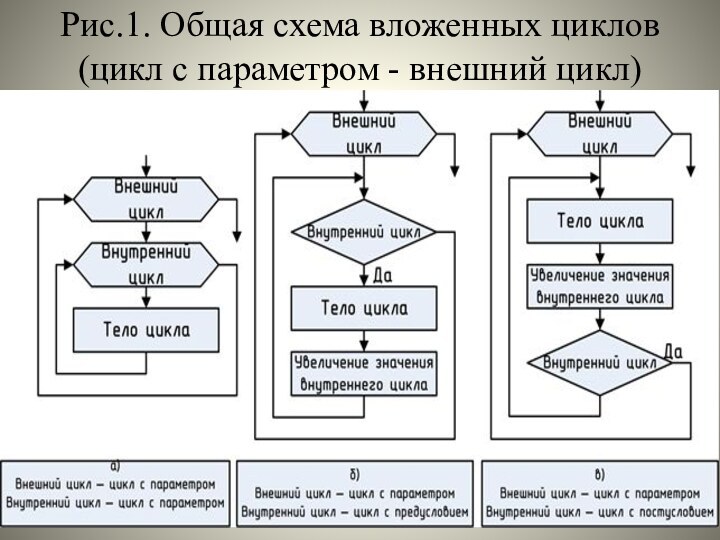
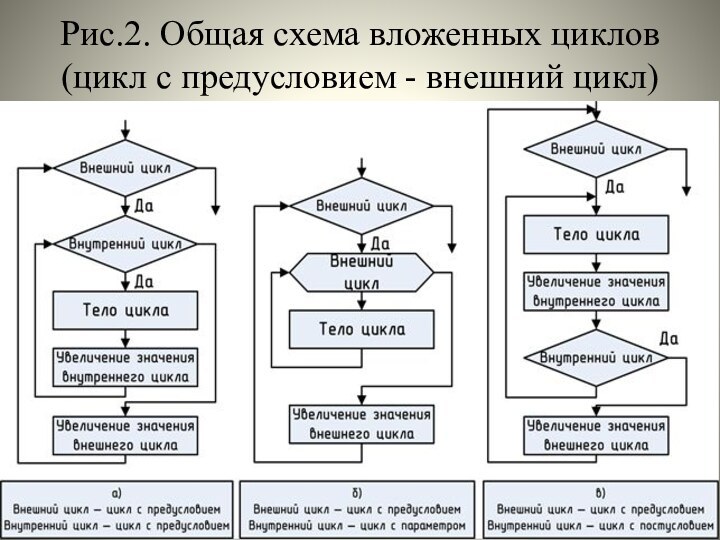
ограничивается только объёмом памяти конкретного ПК, теоретически она не ограничена. Вложенные циклы представляют собой многоуровневую схему, где на каждом уровне управляющая переменная (параметр цикла) может изменяться в соответствии с условием задачи, т.е. в таких задачах можно использовать любой из операторов цикла: For (Рис.1), While (Рис.2), Repeat (Рис.3).
Слайд 22
Рис.1. Общая схема вложенных циклов
(цикл с параметром -
внешний цикл)
Слайд 23
Рис.2. Общая схема вложенных циклов
(цикл с предусловием -
внешний цикл)
Слайд 24
Рис.3. Общая схема вложенных циклов
(цикл с постусловием -
внешний цикл)
Слайд 25
Параметры циклов разных уровней изменяются не одновременно. Вначале
все возможные значения последовательно принимает параметр самого внутреннего цикла
при заданных (неизменных) значениях параметров внешних циклов. После чего на один шаг возрастает параметр цикла на ранг выше внутреннего и при этом вновь переменная внутреннего цикла “пробегает” все свои значения. Такая схема повторяется до тех пор, пока параметры всех циклов не примут все свои возможные значения. Для подсчёта числа повторных вычислений в схеме вложенного цикла можно воспользоваться следующей формулой, если X=Xнач.(Xшаг)Xкон. и Y=Yнач.(Yшаг)Yкон., типа Real: N=NX•NY,
Слайд 26
Рассмотрим несколько примеров проектирования программ с вложенными
циклами.
Слайд 27
Примеры выполнения задания
Пример 1. Найти все простые числа
на заданном отрезке (использовать цикл с параметром)
Для организации
выполнения программы определим целочисленные переменные n, k для обозначения начального и конечного значения отрезка, i, j - для обозначения параметров соответственно внешнего и внутреннего циклов, m-счётчик для количества делителей проверяемого числа.
Слайд 28
Во внешнем цикле последовательно перебираются значения отрезка от
начального до конечного. Во внутреннем цикле параметр j изменяется
от 2 до округлённого значения корня квадратного проверяемого значения, при этом, если остаток от деления числа на параметр j равен нулю, то параметр является делителем данного числа. После каждого завершения работы внутреннего цикла проверяется переменная m, и если она равна нулю, то найдено простое число.
Слайд 29
Program Example_7_1;
Uses Crt; {Подключаем модуль}
Var n : Integer; {Описываем
переменные}
k : Integer; {используемые в программе}
i,j : Integer;
m : Integer;
Begin {Начало
основной программы}
ClrScr; {Команда очистки экрана}
Write ('Введите нижнюю границу отрезка - ');
ReadLn (n); {Вводим данные с клавиатуры}
Write ('Введите верхнюю границу отрезка - ');
ReadLn (k); {Вводим данные с клавиатуры}
WriteLn ('Все простые числа из отрезка [',n,',',k,']');
For i:=n To k do {Задаем внешний цикл}
Begin {Начало внешнего цикла}
m:=0; {Счётчик количества чисел}
Слайд 30
For j:=2 To Round (Sqrt(i)) Do {Задаем внутренний
цикл}
If (i Mod j)=0 Then m:=m+1; {Тело внутреннего цикла}
If m=0
Then Write (i,' ') {Тело внешнего цикла}
End; {Конец внешнего цикла}
End. {Конец основной программы}
Слайд 32
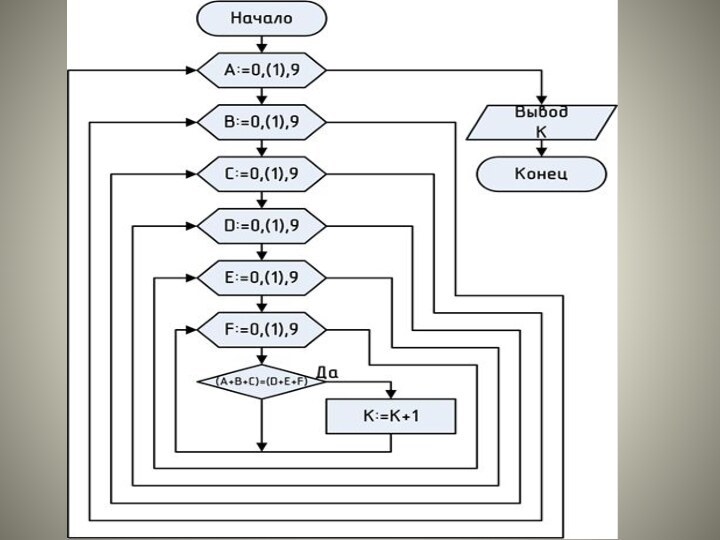
Задача 2. Билет на городском транспорте имеет шестизначную
нумерацию от 000000 до 999999. Билет считается "счастливым", если
сумма трех первых цифр равна сумме трех правых цифр. Составьте алгоритм и напишите программу подсчета числа "счастливых" билетов.
Обозначим через A,B,C,D,E,F соответственно разряды шестизначного числа слева направо. Каждый из разрядов этого числа изменяется от 0 до 9. Все переменные A,B,C,D,E,F являются параметрами цикла. В целом алгоритм можно построить по схеме вложенных циклов. Внешний цикл организуем по переменной А, все другие по B,C,D,E и F будут соответственно вложенными. Самый внутренний цикл организован по F. Далее согласно задаче внутри цикла по F необходим логический блок проверки условия A+B+C=D+E+F. Если оно выполняется, то счетчик числа "счастливых" билетов K=K+1. После чего ветвь "нет" и выход линейного блока K=K+1 объединяются и процесс многократно повторяется.
Слайд 33
Program Example_7_2;
Uses Crt; {Подключаем модуль}
Var
a,b,c,d,e,f: Integer;
{Описываем переменные}
k: Longint; {используемые в программе}
Begin {Начало основной
программы}
ClrScr; {Команда очистки экрана}
For a:=0 To 9 Do {Задаем внешний цикл}
For b:=0 To 9 Do {Задаем внутренний цикл 1}
For c:=0 To 9 Do {Задаем внутренний цикл 2}
For d:=0 To 9 Do {Задаем внутренний цикл 3}
Слайд 34
For e:=0 To 9 Do {Задаем внутренний
цикл 4}
For f:=0 To 9 Do {Задаем
внутренний цикл 5}
If (a+b+c)=(d+e+f) Then k:=k+1;{Проверка на счастливые}
{билеты и подсчет количества}
WriteLn ('k=',k); {Вывод количества счастливых билетов}
End. {Конец основной программы}
Слайд 36
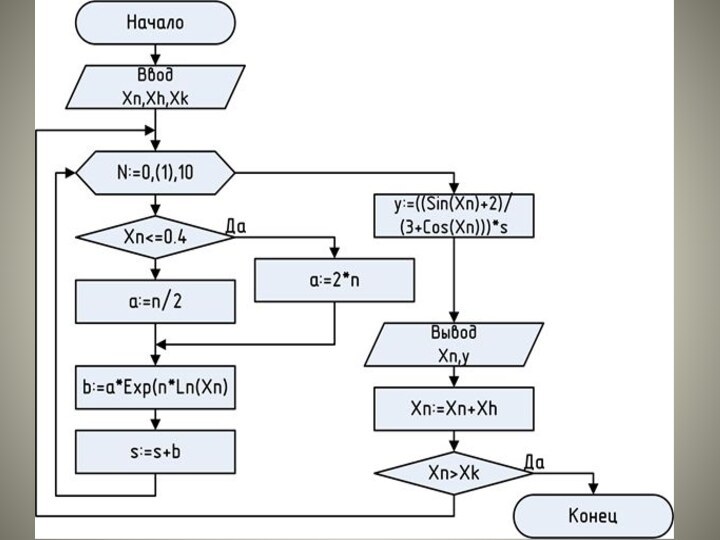
Задача 3. Вычислить таблицу значений функции
Слайд 38
Program Example_7_3;
Uses Crt; {Подключаем модуль}
Va
n: Integer; {Описываем переменные}
x,a,b,s,Xn,Xk,Xh,y: Real; {используемые в программе}
Begin {Начало основной программы}
ClrScr; {Команда очистки экрана}
Write ('Введите Xn,Xh,Xk');{Вывод текста на экран}
Read (Xn,Xh,Xk); {Ввод данных с клавиатуры}
S:=0; {Начальная установка суммы}
Repeat {Внешний цикл}
Слайд 39
For n:=0 to 10 do
{Внутренний цикл}
begin {Начало тела цикла}
If Xn
then {Проверка условия}
a:=2*n {Условие истинно}
else
a:=n/2; {Условие ложно}
b:=a*Exp(n*Ln(Xn)); {Вычисление функции}
s:=s+b; {Суммирование}
End; {Конец внутреннего цикла по N}
Y:=((Sin(Xn)+2)/(3+Cos(Xn)))*s; {Вычисление функции}
WriteLn('X=',Xn,'Y=',Y); {Вывод значений функций}
Xn:=Xn+Xh {Увеличение значения внешнего}
{цикла на значение шага}
Until Xn>Xk; {Проверка истинности}
{внешнего цикла}
End. {Конец основной программы}