Слайд 2
Вопросы
Причинность, регрессия, корреляция
Задачи и предпосылки применения корреляционно-регрессионного анализа
Парная
регрессия на основе метода наименьших квадратов и метода группировок
Множественная
(многофакторная) регрессия
Оценка значимости параметров взаимосвязи
Слайд 3
Причинно-следственные отношения
- Это связь явлений и процессов, при
которой изменение одного из них - причины - ведет
к изменению другого - следствия.
Причина - это совокупность условий, обстоятельств, действие которых приводит к появлению следствия
Слайд 4
Причинно-следственные отношения
Признаки, обуславливающие изменения других, связанных с ними
признаков, называются факторными, или факторами.
Признаки, изменяющиеся под действием
факторных признаков, являются результативными.
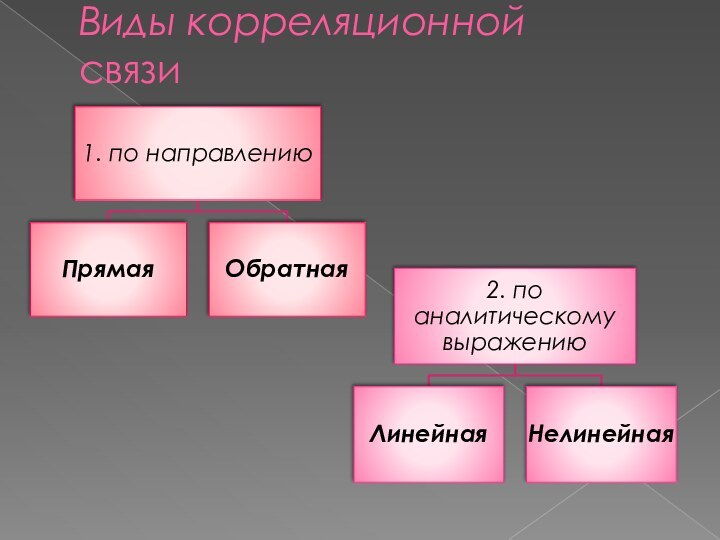
Связи между явлениями и их признаками классифицируются по степени тесноты, направлению и аналитическому выражению.
Слайд 5
Причинно-следственные отношения
Если причинная зависимость проявляется в общем, среднем
при большом числе наблюдений, то зависимость называется стохастической.
Частный
случай стохастической зависимости - корреляционная связь
Слайд 6
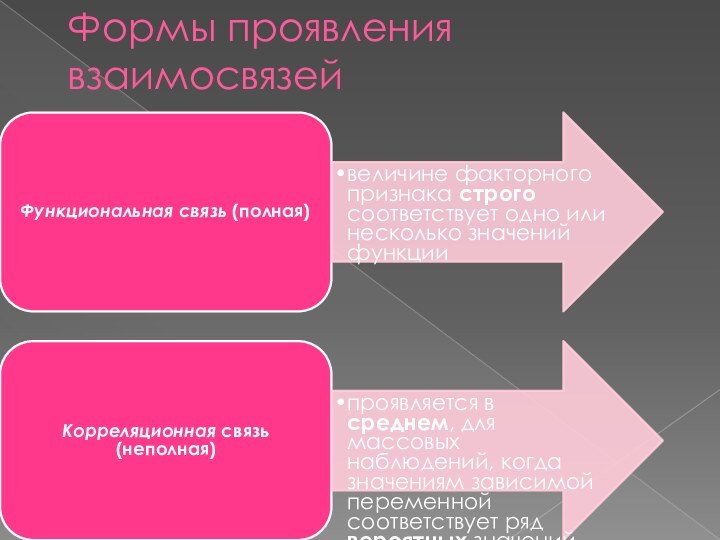
Формы проявления взаимосвязей
Слайд 7
Корреляционная связь
-существует когда изменение среднего значения результативного признака
обусловлено изменением факторных признаков.
Слайд 8
При корреляционной связи:
Связь между признаками проявляется лишь
в среднем, в массе случаев.
Каждому значению аргумента соответствуют
случайно распределенные в некотором интервале значения функции.
Слайд 9
Корреляционно-регрессионный анализ
Включает в себя:
1. измерение тесноты и направления
связи корреляционный
анализ
2. установление аналитической формы связи (формы зависимости признаков)
регрессионный
анализ
Слайд 11
Корреляционный метод
количественное определение тесноты связи между двумя признаками
(при парной связи) и между результативным и множеством факторных
признаков (при многофакторной связи).
Корреляция - это статистическая зависимость между случайными величинами, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
Слайд 12
Регрессионный метод
аналитическое определение связи, в котором изменение одной
величины (результативного признака) обусловлено влиянием одной или нескольких независимых
величин (факторов), при этом множество прочих факторов, также влияющих на зависимую величину, принимается за постоянные и средние значения.
Слайд 14
Парная корреляция и парная регрессия
характеризует связь между двумя
признаками – результативным (Y) и факторным (X)
Слайд 15
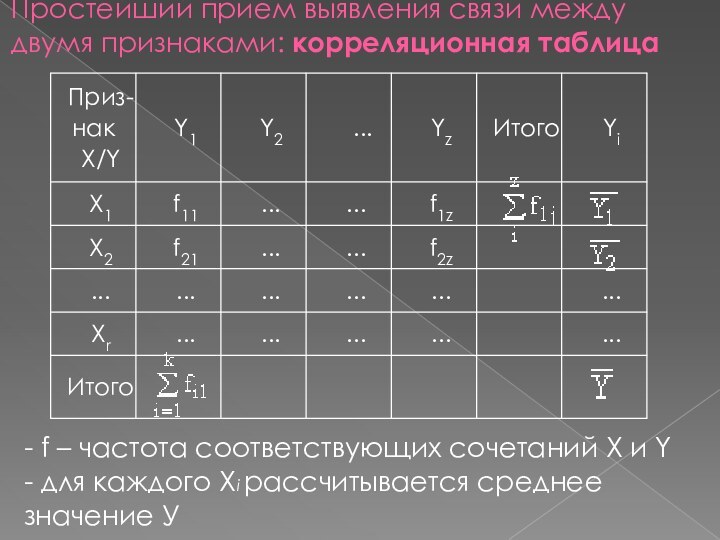
Простейший прием выявления связи между двумя признаками: корреляционная
таблица
- f – частота соответствующих сочетаний X и
Y
- для каждого Хi рассчитывается среднее значение У
Слайд 16
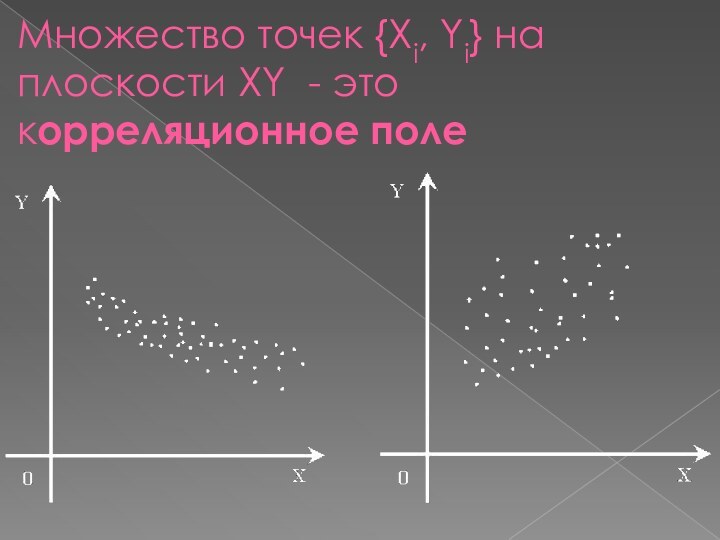
Множество точек {Xi, Yi} на плоскости XY -
это корреляционное поле
Слайд 17
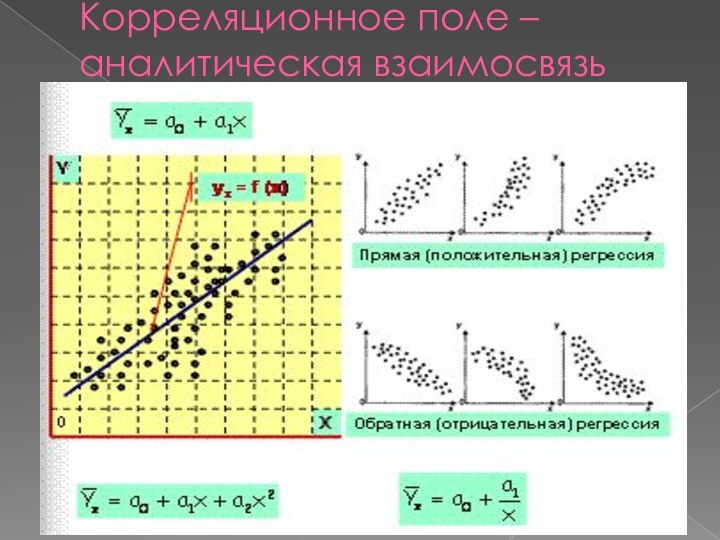
Корреляционное поле – аналитическая взаимосвязь
Слайд 18
Аналитическая связь (форма) между двумя признаками - описывается
уравнениями:
Слайд 19
Коэффициент корреляции
Количественная оценка тесноты связи
Характеризует тесноту
и направление связи между двумя признаками в случае наличия
между ними линейной зависимости
Слайд 20
Коэффициент корреляции принимает значения от -1 до +1
r
> 0 – связь прямая
r < 0 –
связь обратная
|r| < 0,30 - связь слабая
|r| = 0,3…0,7 - связь средняя
|r| > 0,70 - связь сильная, или тесная
|r| = 1 - связь функциональная, т.е. каждому значению факторного признака строго соответствует одно значение результативного признака
r близко к 0 - отсутствует линейная связь между У и X (возможно нелинейное взаимодействие)
Слайд 21
Метод наименьших квадратов
Сущность метода: нахождение параметров модели (а0,
а1), при которых минимизируется сумма квадратов отклонений фактических значений
результативного признака от теоретических
Слайд 22
Метод наименьших квадратов
Сущность метода: нахождение параметров модели (a,
b), при которых минимизируется сумма квадратов отклонений фактических значений
результативного признака от теоретических
Слайд 23
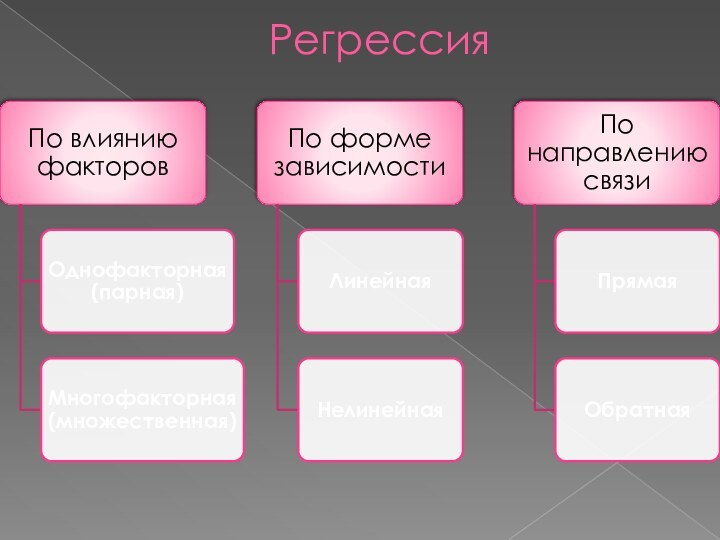
Множественная (многофакторная) регрессия
Изучение связи между тремя и более
связанными между собой признаками.
Аналитическое определение связи между результативным признаком
и множеством факторных признаков, т.е нахождение функции:
Слайд 24
Метод перебора различных уравнений
Сущность заключается в том, что
большое число уравнений (моделей) регрессии, отобранных для описания связей
какого-либо социально-экономического явления или процесса, реализуется на ЭВМ с помощью специально разработанного алгоритма перебора с последующей статистической проверкой, главным образом, на основе t - критерия Стьюдента и F-критерия Фишера-Снедекора.
Слайд 25
Оценка значимости и правильности параметров взаимосвязи
Получив значения корреляции
и уравнение регрессии - необходимо проверить их на соответствие
истинным параметрам взаимосвязи:
При этом:
1) значимость коэффициента корреляции проверяется на основе
t– критерий Стьюдента
2) правильность выбора вида взаимосвязи и всего уравнения регрессии проверяется на основе
F– критерий Фишера
Слайд 26
Оценка значимости параметров корреляции: t– критерий Стьюдента
Значимость
коэффициента корреляции проверяется на основе
t- критерия Стьюдента.
При
этом выдвигается и проверяется нулевая гипотеза о равенстве коэффициента корреляции нулю (r=0), т.е гипотеза об отсутствии взаимосвязи.
При проверке этой гипотезы используется
t-статистика (из специальных таблиц).
Слайд 27
Оценка значимости параметров взаимосвязи: t– критерий Стьюдента
где
tрасч –расчетное значение t-критерия.
Eсли расчетное значение tр > tкр
(табличное), то гипотеза отвергается , что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической зависимости между Х и У
Слайд 28
Оценка значимости параметров взаимосвязи: F– критерий Фишера
Вывод
о правильности выбора вида взаимосвязи и характеристику значимости всего
уравнения регрессии получают с помощью
F-критерия.
При этом выдвигается и проверяется нулевая гипотеза о несоответствии заложенных в уравнении регрессии связей реально существующим.
Слайд 29
Оценка правильности выбора вида взаимосвязи и уравнения регрессии
: F– критерий Фишера
Если Fр>Fα при α =
0,05 или α = 0,01, то гипотеза о несоответствии заложенных в уравнении регрессии связей реально существующим отвергается.
Величина Fα определяется по специальным таблицам, входом в которые являются величины α = 0,05 или α = 0,01 и числа степеней свободы: v1 = k -1, v2 = n -k, где n - число наблюдений,
k - число факторных признаков в уравнении
Слайд 30
Измерение связи между качественными признаками
Слайд 32
Коэффициент ассоциации
Зависимости
a, b, c, d - значения признаков
в клетках матрицы сопряженности альтернативных признаков
Слайд 33
Коэффициент ассоциации
принимает значения от -1 до +1
Если коэффициент
имеет положительный знак (+), то связь положительная,
Если коэффициент имеет
отрицательный знак
(-), то связь отрицательная.
Кас = 0 - корреляция отсутствует (данные факторы между собой нейтральны);
0,09 ≤ Кас ≤ 0,19 - статистическая взаимосвязь очень слабая;
- если 0,2 ≤ Кас ≤ 0,49 - статистическая взаимосвязь слабая;
- если 0,5 ≤ Кас ≤ 0,69 - статистическая взаимосвязь средняя;
- если 0,70 ≤ Кас ≤ 0,99 - статистическая взаимосвязь сильная.
Слайд 34
Коэффициент контингенции (сопряженности)
В отличие от коэффициента ассоциации
он учитывает двустороннюю взаимосвязь альтернативных признаков, т.е. производит измерение
более чутко и корректно.
Слайд 35
Коэффициент детерминации
зависимости