Презентация на тему Задачи с параметрами

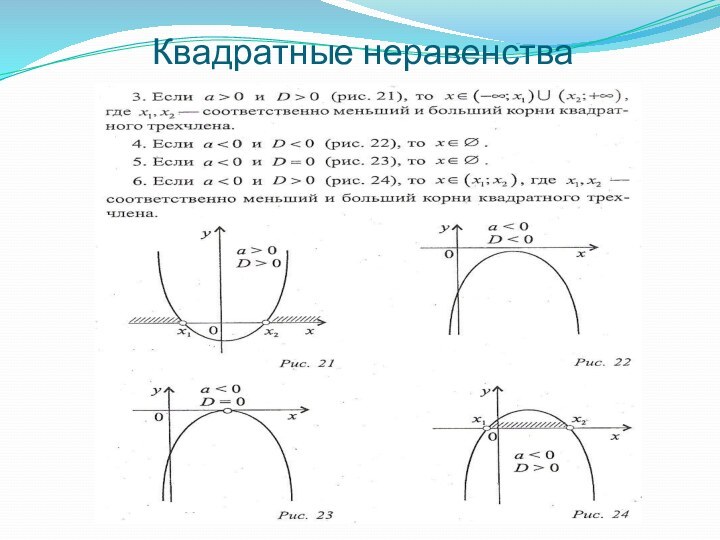
и совокупности, которые необходимо решить либо для любого значения

параметра, либо для значений параметра, принадлежащих заранее оговоренному множеству
Уравнения, неравенства, их системы и совокупности, для которых требуется определить количество решений в зависимости от значения параметра
Уравнения, неравенства, их системы и совокупности, для которых требуется найти все те значения параметра, при которых указанные уравнения (…) имеют заданное число решений
Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.

способ так называемого прямого решения, повторяющего стандартные процедуры нахождения

ответа в задачах с без параметров.
(графический). В зависимости от задачи (с переменной х и параметром а) рассматриваются графики или в координатной плоскости (х;у), или в координатной плоскости (х;а)
(решение относительно параметра). При решении этим способом переменные х и а принимаются равноправными и выбирается та переменная , относительно которой аналитическое решение признается наиболее простым. После естественных упрощений возвращаемся к исходному смыслу переменных х и а и заканчиваем решение.

|х2-2ах|=1 имеет три различных корня?
Решение:
Данное уравнение равносильно совокупности двух

уравнений х2-2ах =1 и х2-2ах = -1
1) уравнение х2-2ах -1=0 при любых значениях а имеет два различных корня х1,2 , т.к. D = 4a2+4>0
2) если у уравнения х2-2ах = -1 есть два корня х3,4, то поскольку они не могут совпадать с х1,2 , исходное уравнение имеет три корня тогда и только тогда, когда уравнение х2-2ах +1=0 имеет кратный корень, что равносильно условию D = 4a2- 4 = 0, откуда а=±1.
Ответ: а=±1

которых уравнение ||х| + a - 9| = а2

имеет ровно 3 корня. Если таких значений а более одного, в ответе укажите их произведение.

Решаем данное уравнение графически.
На рис. 2а изображён эскиз графика у = |х| + a - 9,
а на рис.2б — эскиз графика у = ||х| + a - 9| и прямой у = а2 (предполагаем, что а - 9 < 0, т.к. если а - 9 > 0, то
||х| + а - 9| = |х| + а - 9, при этом данное в условии уравнение принимает вид |х| = а2 - а + 9 и имеет не более двух корней).





Из рис.2б следует, что график у = ||х| + а - 9| и прямая у = а2
имеют ровно три общие точки а2 = 9 - а, а2 + а - 9 = 0. Полученное
квадратное уравнение имеет два корня, произведение которых по теореме Виета равно -9.
Ответ: -9.

(2а-1)х2

Решение:

Пусть дан квадратный трехчлен f(x)=ax2+bx+c, a≠0, и некоторое действительное

число d. Если для f(x) выполняются следующие условия:


, то он имеет два действительных корня х1 и х2, меньших числа d.

Пусть дан квадратный трехчлен f(x)=ax2+bx+c, a≠0, и некоторое действительное

число d. Если для квадратного трехчлена f(x) выполняются следующие условия:


то он имеет два действительных корня х1 и х2, больших числа d.

Т1 и 2
Пусть даны два действительных числа d1

и d2. Если для квадратного трехчлена f(x) выполняются следующие условия:



то он имеет два действительных корня х1 и х2, принадлежащих промежутку (d1;d2)

Пусть дано некоторое действительное число d. Если для квадратного

трехчлена f(x) выполняется условие


то он имеет два действительных корня х1 и х2, расположенных по разные стороны от числа d.

Пусть даны два действительных числа d1 и d2 :

d1 < d2. Если для квадратного трехчлена f(x) выполняется условие
, то квадратный трехчлен f(x) имеет два действительных корня, один из которых принадлежит промежутку (d1;d2), а другой не принадлежит промежутку [d1;d2] .

Пусть даны два действительных числа d1 и d2 :

d1 < d2. Если для квадратного трехчлена f(x) выполняются условия

, то квадратный трехчлен f(x) имеет два действительных корня, один из которых меньше числа d1, а второй – больше числа d2