- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике Функциональные методы решения уравнений и неравенств
Содержание
- 2. Обоснование актуальности темы: Один из основных
- 3. Цель: изучение функциональных методов решения уравнений и неравенств
- 4. Задачи:повторить свойства функций, изучаемых
- 5. Использование понятия области определения функцииОбластью определения
- 6. Решить уравнение Решение. ОДЗ:
- 7. Решить уравнение Решение. ОДЗ: Проверка: х = 1, 0=0х = 3 - неверное равенствоОтвет: 1.
- 9. Решить уравнение sin x+sin 9x=2.Решение.Ответ:
- 10. Решить уравнение Решение. Выделим
- 11. Использование свойств монотонности функцийФункцию y =
- 12. Сформулируем теоремы о корнеТеорема 1
- 13. Решить уравнение Решение. ОДЗ: х≤2,25.
- 14. Найти значение выражения
- 15. Скачать презентацию
- 16. Похожие презентации
Обоснование актуальности темы: Один из основных критериев обученности сегодня — это результаты ЦТ. Но для того, чтобы успешно справиться с заданиями, предлагающимися на ЦТ, школьной программы недостаточно. Необходимы дополнительные материалы. Именно поэтому было проведено исследование по теме














Слайд 4
Задачи:
повторить свойства функций, изучаемых в
курсе математики;
описать суть каждого свойства, дать рекомендации по его
использованию, указания к применению;провести некоторую классификацию нестандартных уравнений (неравенств) по использованию общих свойств функций.
Слайд 5
Использование понятия области
определения функции
Областью определения функции y
= f(x) называется множество значений переменной х, при которых
функция имеет смысл.Пусть дано уравнение f(x) = g(x), где f(x) и g(x)- элементарные функции, определенные на множествах D1, D2. Тогда областью определения уравнения будет множество, состоящее из тех значений х, которые принадлежат обоим множествам, то есть D = D1 D2. Ясно, что когда множество D пустое (D=Ø), то уравнение решений не имеет.
Слайд 6
Решить уравнение
Решение. ОДЗ:
Так как полученная система решений не имеет,
то область определения уравнения не содержит ни одного числа. Значит данное уравнение не имеет решений.Ответ: решений нет.
Слайд 8
Использование ограниченности функций
Областью значений функции y = f(x)
называется множество значений переменной y при допустимых значениях переменной
x.Функция y = f(x) называют ограниченной снизу (соответственно сверху) на множестве Х, если существует такое число М, что на Х выполняется неравенство f(x) ≥ M (соответственно ) .
Число М называется мажорантой данной функции.
Пусть мы имеем уравнение f(x) = g(x) и существует такое число M, что для любого x из области определения f(x) и g(x) имеем: и , , тогда уравнение f(x) = g(x) эквивалентно системе:
Слайд 10
Решить уравнение
Решение. Выделим полный квадрат
в правой части уравнения, т.е.
Так как при этом , то получаем систему
yравнений
x=
Ответ: x = .
Слайд 11
Использование свойств
монотонности функций
Функцию y = f(x) называют
возрастающей (соответственно убывающей) на множестве Х, если на этом
множестве при увеличении аргумента увеличиваются (соответственно уменьшаются) значения функции.
Слайд 12
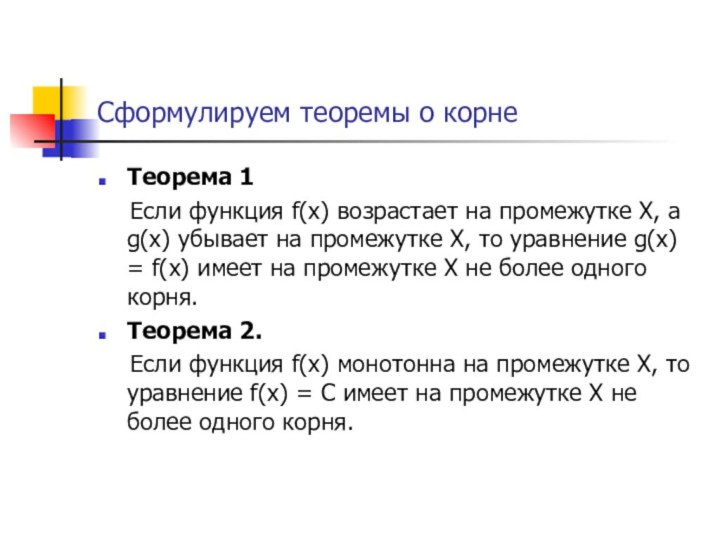
Сформулируем теоремы о корне
Теорема 1
Если
функция f(x) возрастает на промежутке Х, а g(x) убывает
на промежутке Х, то уравнение g(x) = f(x) имеет на промежутке Х не более одного корня.Теорема 2.
Если функция f(x) монотонна на промежутке Х, то уравнение f(x) = С имеет на промежутке Х не более одного корня.
Слайд 13
Решить уравнение
Решение. ОДЗ: х≤2,25.
Так
как f(x)=
- убывающая функция,а g(x)= - возрастающая функция на области определения, то по теореме о корне уравнение имеет не более одного корня.
Подбором находим х=2.
Ответ: 2.
Слайд 14 Найти значение выражения
, где n – количество корней,
- целый корень уравненияРешение. Рассмотрим функции f(x)= и g(x)= .
Функция f(x) убывает на множестве действительных чисел, а функция g(x) - возрастает на множестве действительных чисел. По теореме о корне уравнение имеет не более одного корня. Найдём его подбором: х=3. Значит это единственный корень уравнения, т.е. n=1.
=1•3=3.
Ответ: 3.