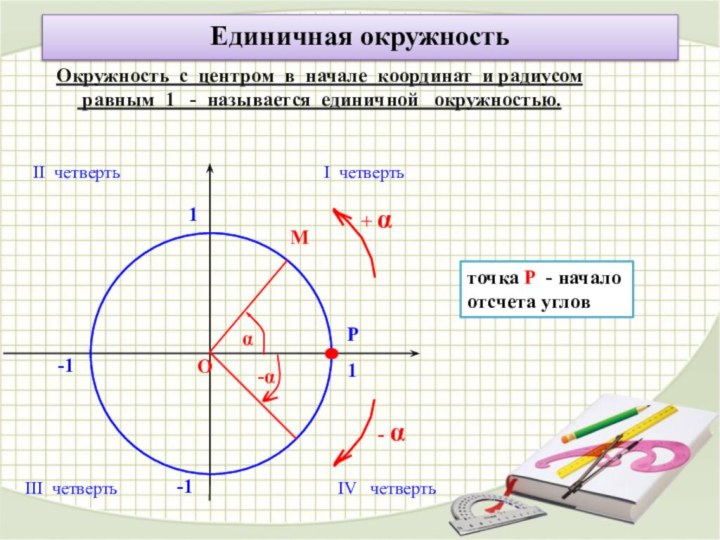
радиусом
равным 1 - называется единичной
окружностью. О
Р
1
1
-1
-1
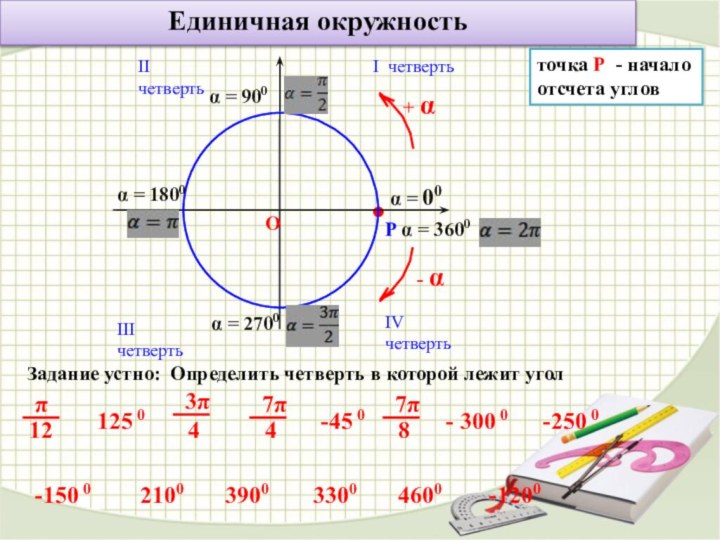
точка Р - начало отсчета углов
М
α
+ α
- α
I четверть
II четверть
III четверть
IV четверть
-α
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

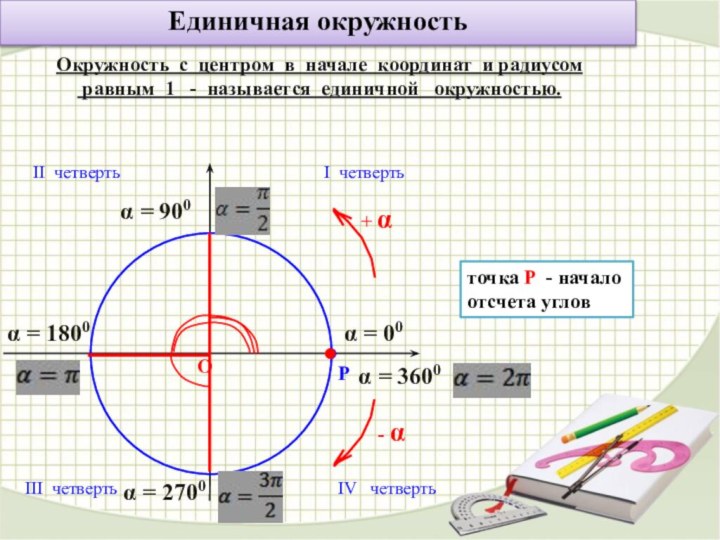


О
Р
1
1
-1
-1
точка Р - начало отсчета углов
М
α
+ α
- α
I четверть
II четверть
III четверть
IV четверть
-α
О
Р
точка Р - начало отсчета углов
+ α
- α
I четверть
II четверть
III четверть
IV четверть
α = 00
α = 900
α = 1800
α = 2700
α = 3600
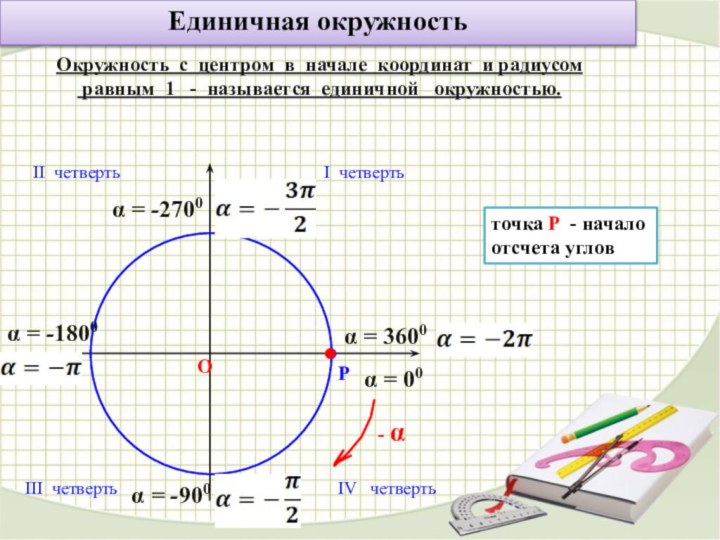
О
Р
точка Р - начало отсчета углов
- α
I четверть
II четверть
III четверть
IV четверть
α = 00
α = -900
α = -1800
α = -2700
α = 3600
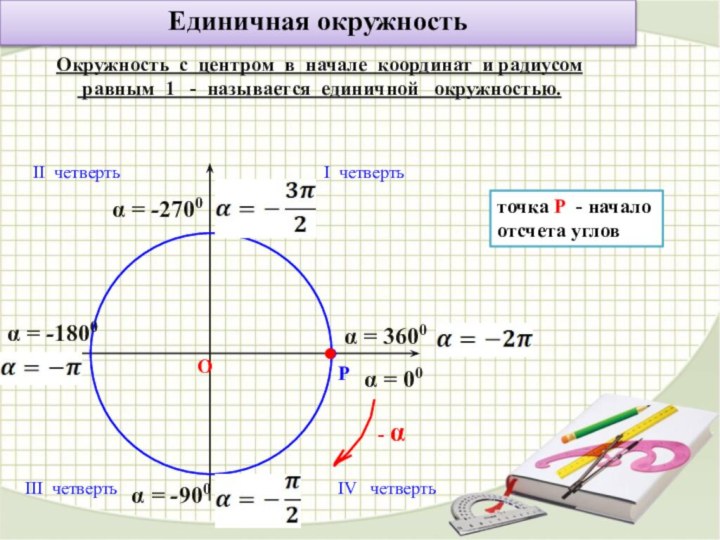
О
Р
точка Р - начало отсчета углов
- α
I четверть
II четверть
III четверть
IV четверть
α = 00
α = -900
α = -1800
α = -2700
α = 3600
- 300 0
-250 0
-150 0
2100
3300
3900
4600
-1200
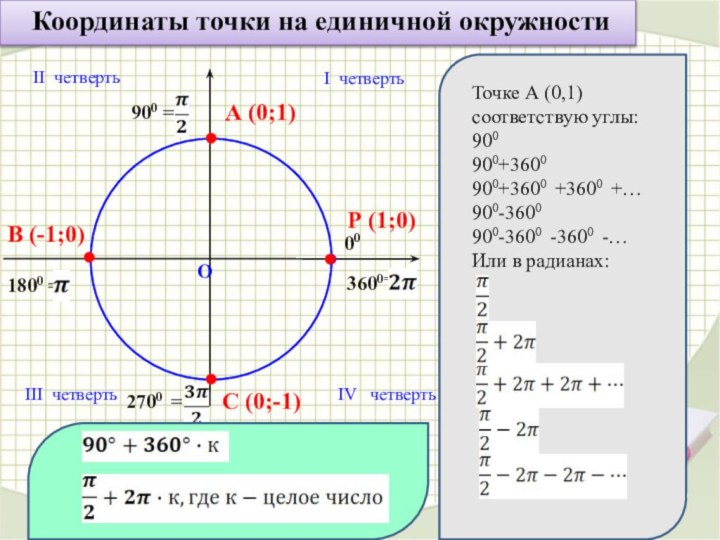
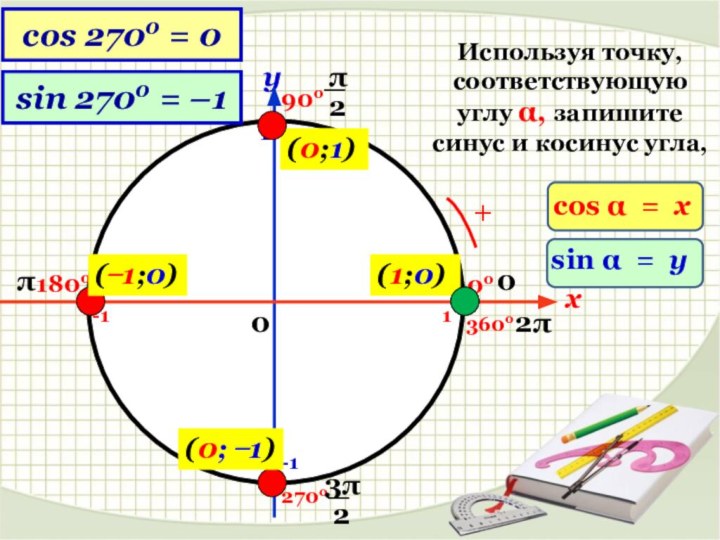
А (0;1)
В (-1;0)
С (0;-1)
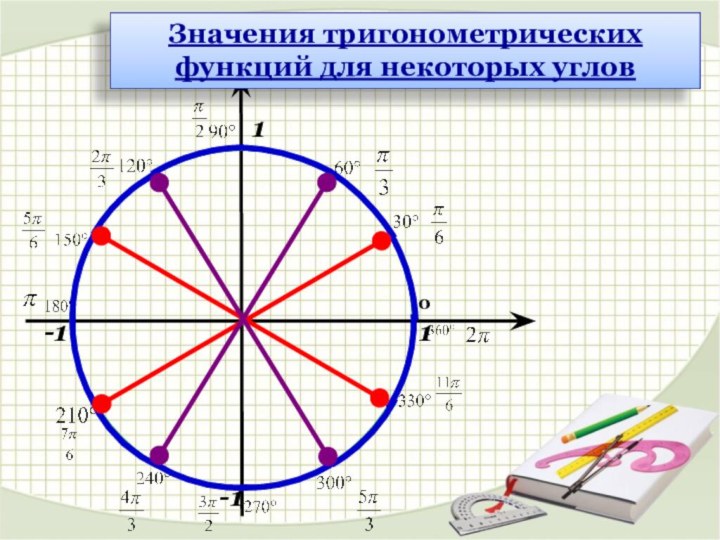
Точке А (0,1) соответствую углы:
900
900+3600
900+3600 +3600 +…
900-3600
900-3600 -3600 -…
Или в радианах:
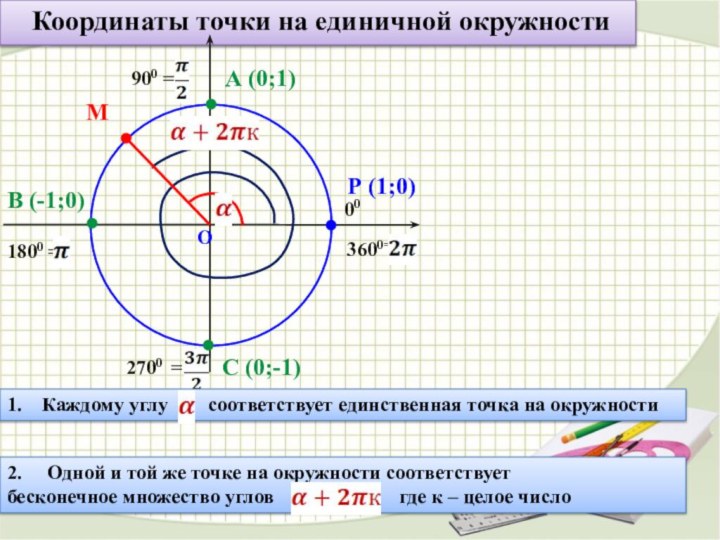
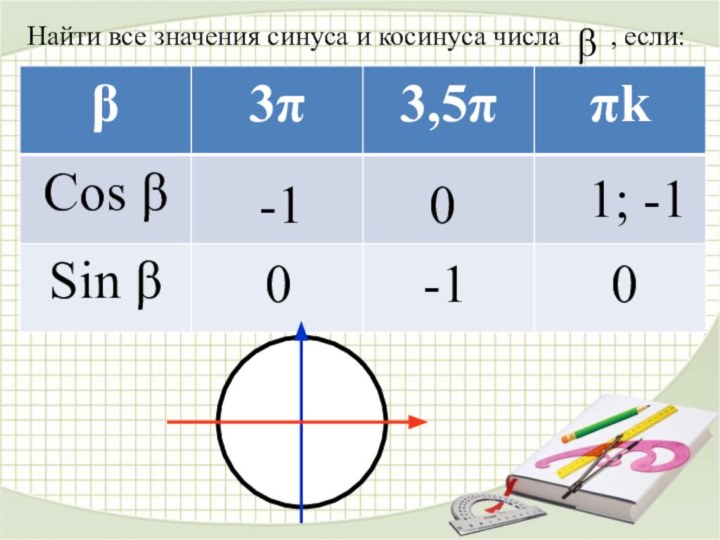
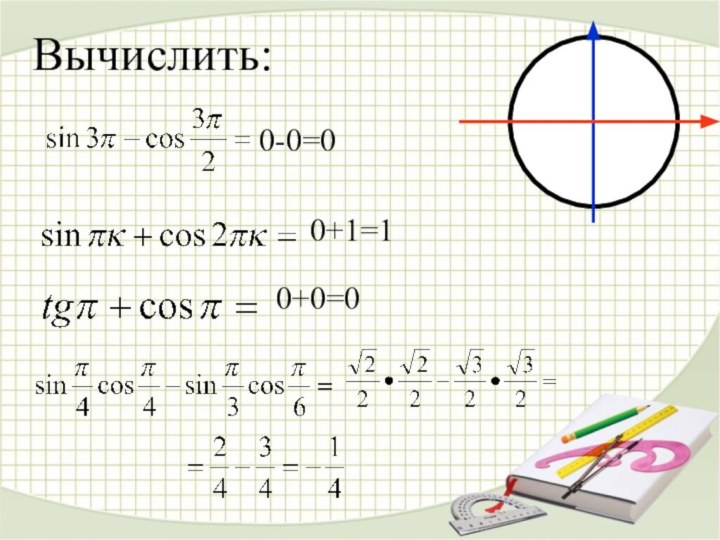
2. Одной и той же точке на окружности соответствует бесконечное множество углов где к – целое число
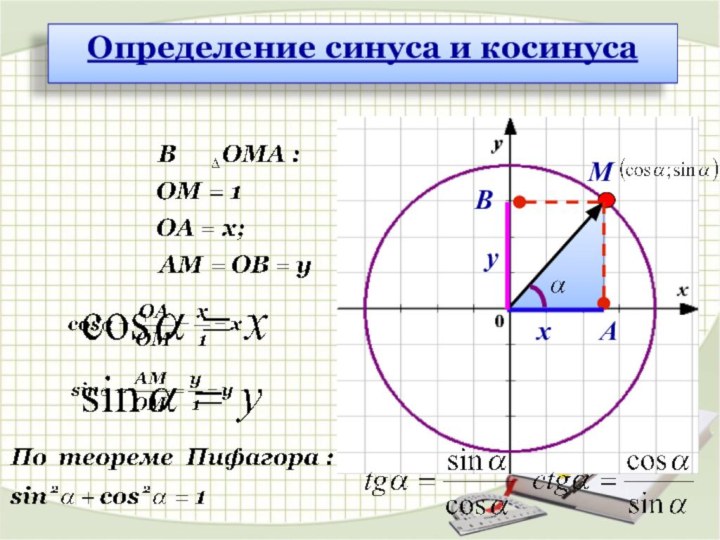
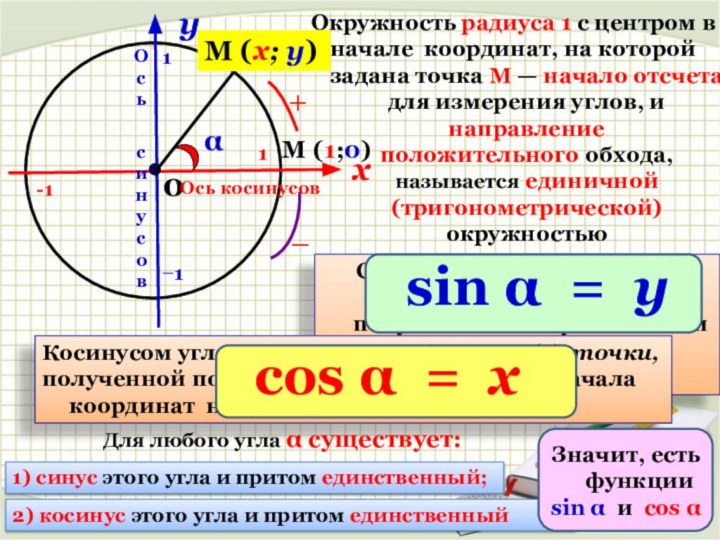
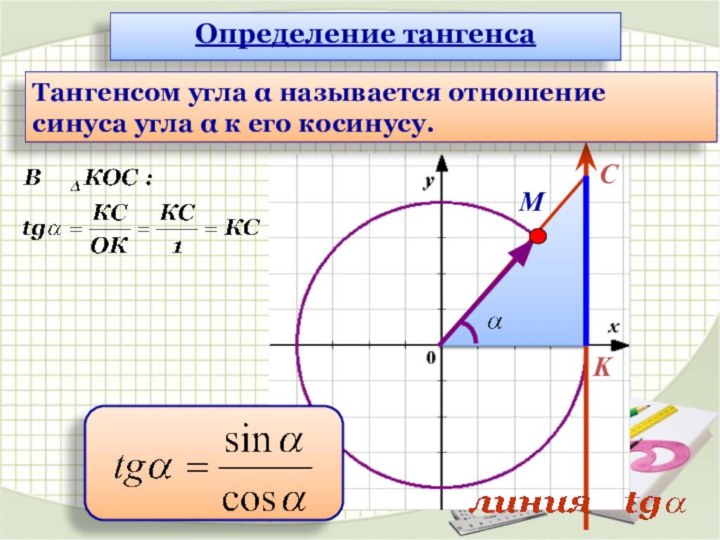
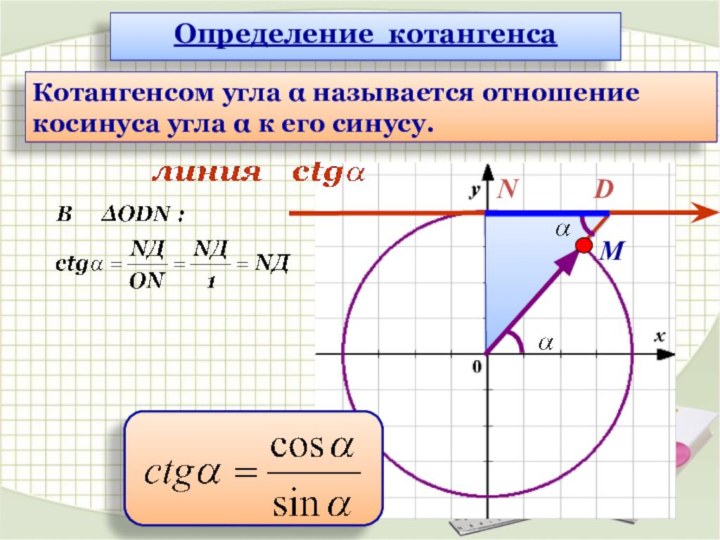
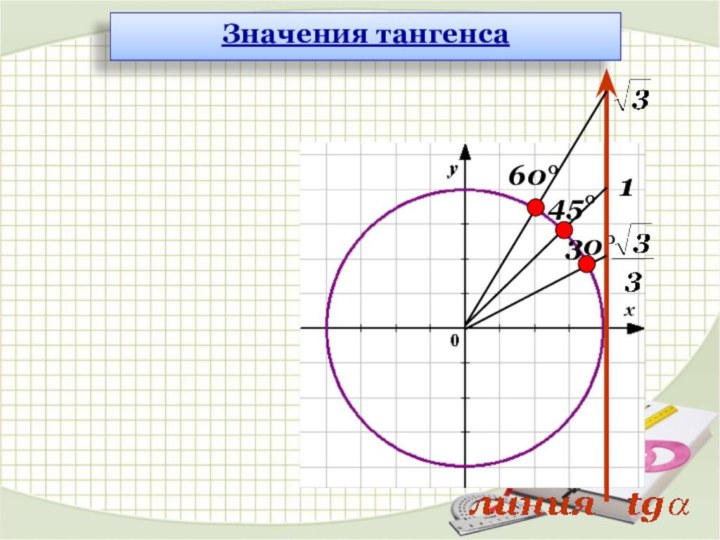
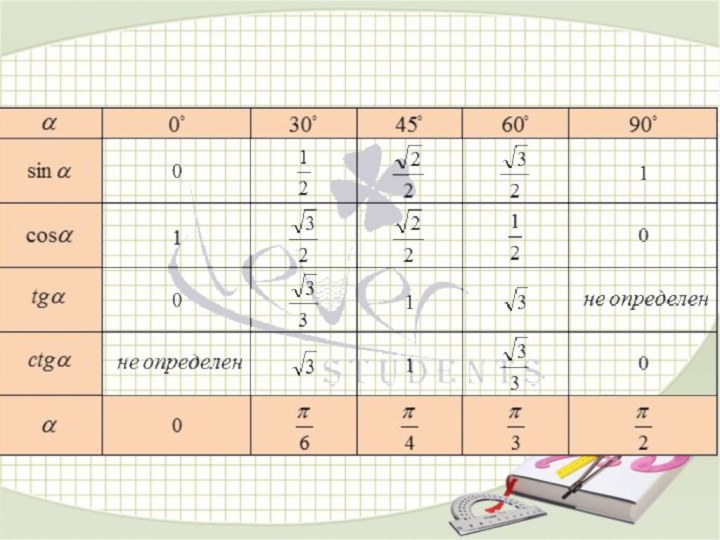
Синусом угла α называется
ордината (у) точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α
М (x; y)
1
-1
1
̶ 1
α
М (1;0)
+
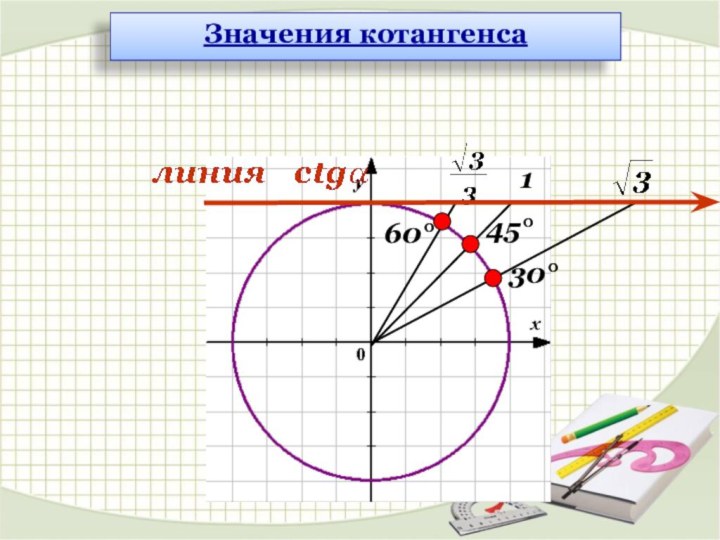
Косинусом угла α называется абсцисса (х) точки,
полученной поворотом точки (1; 0) вокруг начала координат на угол α
Для любого угла α существует:
1) синус этого угла и притом единственный;
2) косинус этого угла и притом единственный
̶
Ось
синусов
Ось косинусов
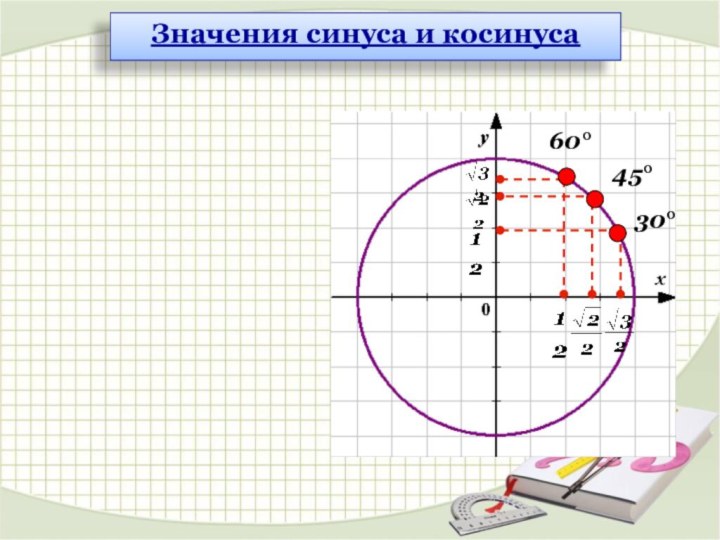
cos 00 = 1
sin 900 = 1
cos 900 = 0
cos 1800 = –1
sin 1800 = 0
cos 2700 = 0
sin 2700 = –1