Презентация на тему к уроку математики в 8 классе Квадратные уравнения

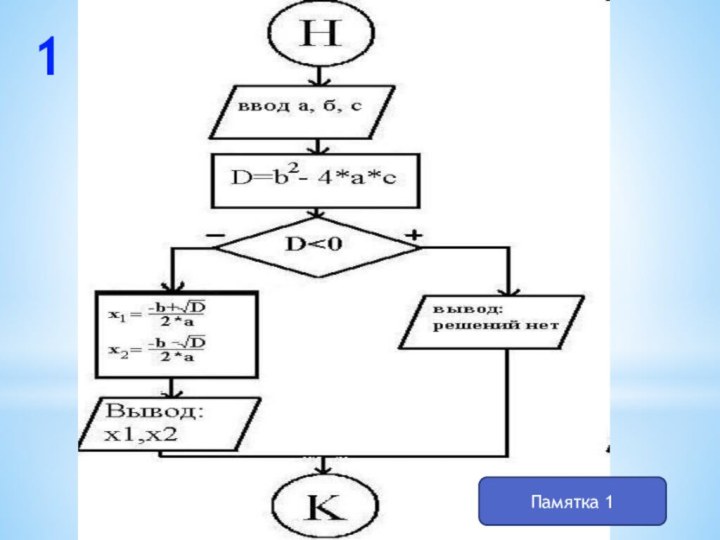
знать формулы корней квадратного уравнения, теорему Виета, уметь решать

квадратные уравнения всех видов - неполные, приведенные, полные.
Развивающая цель: Развивать память, мышление учащихся, вычислительные навыки, интерес к предмету, коммуникативность, навыки самостоятельной работы.
Воспитательная цель: воспитание самостоятельности учащихся, взаимопомощи при групповой работе; правильной самооценки своих работ.

Цели урока

“Квадратные уравнения”.
Проверка домашнего задания
Проверочная работа на компьютере
Повторение учебного материала

. Решение квадратных уравнений по формуле
. Решение квадратных уравнений по формуле D1
. Решение квадратных уравнений разложением левой части уравнения на множители
Метод выделения полного квадрата
Решение уравнений с использованием теоремы Виета(прямой и обратной)
Решение уравнений методом «переброски»
Решение уравнений, применяя свойство коэффициентов квадратного уравнения
Графическое решение квадратных уравнений
Физминутка «супер физкультминутка»
Закрепление изученного материала
Итог.
Оценка
Домашняя работа

План урока

первый коэффициент равен ­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­1
3. Уравнения с одной переменной,

имеющие одни и те же корни
4.Числа а,в и с в квадратном уравнении
5.Значение переменной, при котором уравнение обращается в верное равенство 6. Коэффициент с квадратного уравнения
7.Неотрицательное значение квадратного корня
8. Древнегреческий математик, который нашел приемы решения квадратных уравнений без обращения к геометрии
9. Квадратное уравнение, в котором хотя бы один из коэффициентов в или с равен 0
10. Французский математик, который вывел формулы, выражающие зависимость корней уравнения от его коэффициентов

квадратного уравнения

Чтобы решить квадратное уравнение, достаточно:
1) вычислить дискриминант и

сравнить его с нулем;
2) если дискриминант положителен или равен нулю, то воспользоваться формулами для вычисления корней
3) если дискриминант отрицательный, то записать, что корней нет.

квадратного уравнения
Памятка 1

Памятка 5.doc

Пусть дано квадратное уравнение
ax2

+bx +c=0 , где а ≠ 0
Если a+b+c=0 (т.е. сумма коэффициентов уравнения равна нулю), то х1= 1,

Если, а-b+с=0, или b= a+c
то, х1= -1,

построить графики функций
y = f(x), y = g(x)

и найти точки их пересечения;
абсциссы точек пересечения и будут корнями уравнения.

Пример:

8 способ

=0
Координаты вершины xb=-b/2a=1 yb= -4
Найти точки абсциссы

которых симметричны относительно х=1
Построить по таблице график
y=x2 -2x -3

Примеры графического решения квадратных уравнений

3

-1

Решение уравнения x2-2x –3=0

Корни уравнения равны абсциссам точек пересечения параболы с осью ОХ