Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему к уроку обобщение и систематизация знаний по теме Решение уравнений в 9 классе.

Содержание

Цель урока: Обобщить и систематизировать знания по теме « Решение уравнений с одной переменной»
Цель урока: Обобщить и систематизировать знания по теме « Решение Виды уравнений с одной переменной Рациональные уравнения Целые Определение линейного уравненияУравнение вида aх = b (где х – переменная, а Решите устно:1. 14x=-72. 3x=03. |x|=84. |x|+9=85. 0x=06. 0x=2,37. 8. |x-6|=5 x-6=5 или x-6=-5   Корнем уравнения 6-х-3(2-5х)=12+8х является число   Сколько корней имеет уравнение? 6(1,2х-0,5)- 1,3х=5,9х -3 Закончи предложение:Формула корней квадратного уравнения…Формула корней кв. уравнения с чётным вторым коэффициентом Приведённое квадратное уравнение x2+px+q=0 Как можно решить приведённое квадратное уравнение, Теорема Виетаx2+px+q=0x1+x2=-px1·x2=qФормула разложения квадратного трёхчлена на множители:аx2+bx+c=a(x-x1)(x-x2) где x1, x2 – корни квадратного трёхчлена «Верно-неверно» Тест Определите, верны ли высказывания ?ЕДВИСКРИМИВНЕАНВТАКорни уравнения 2x2-32=0 являются противоположными числами Тест: «Верно – неверно»ЕДВИСКРИМИВНЕАНВТИОдин из корней уравнения x2-x√3=0 является иррациональным числом Тест: «Верно – неверно»ЕДВИСКРИМИВНЕАНВТККорнями уравнения x2-100x+99=0 являются числа 1и 99 Тест: «Верно – неверно»ЕДВИСКРИМИВНЕАНВТСУравнение x2-6x+1-√2=0 имеет два различных корня Тест: «Верно – неверно»ЕДВИСКРИМИВНЕАНВТЕКорнем уравнения x(x-3,5)=2(x-3,5)является число -2 Тест: «Верно – неверно»ДВИСКРИМИВНАНВТНСумма корней уравнения Тест: «Верно – неверно»ДВИСКРИМИВНАНВТМУравнение x2 -10x+25=0 имеет один корень Тест: «Верно – неверно»ДВИСКРИМИВНАНВТРЧисла x1 и x2 ,изображенные на координатной прямой, Тест: «Верно – неверно»ДВИСКРИМИВНАНВТВУравнение 4x2 +25=0 имеет два корня Физкультминутка Посчитай до десяти. Будь внимателен!Что пропало? у=2х; х=3 ; у=4; х=-5; у=-8;  Алгоритм решения уравнений графическим способомИз уравнения выделяем знакомые нам функции.Строим графики функций в одной координатной  На рисунке изображены графики функций у = х3 и у = –2 На рисунке изображены графики функций у = – х2 + 2 и Уравнение вида ах⁴+bх²+с=0, где а, b и с –данные числа и Алгоритм решения биквадратного уравненияДелаем замену переменной Составляем и решаем квадратное уравнение с Решите биквадратное уравнение Вариант 1 Определение Дробным рациональным уравнением называют уравнение, обе части которого являются рациональными выражениями, причём Решите дробно – рациональные уравненияНет корнейy=-5y=-15 - найти общий знаменатель дробей, входящих в уравнение;- Решите уравнение: Самостоятельная работа Проверь себя: Проверь себя: Проверь себя: Дробно-рациональные: 1) х=-1,2; Домашнее задание:Вариант 1-15 №9 На сегодняшнем уроке: - Я благодарю за сотрудничество… .
Слайды презентации

Слайд 2

Слайд 3

Слайд 4

Слайд 5 Цель урока: Обобщить и систематизировать знания по теме

Цель урока: Обобщить и систематизировать знания по теме « Решение уравнений с одной переменной»

« Решение уравнений с одной переменной»

Слайд 6 Виды уравнений с одной переменной
Рациональные уравнения

Целые

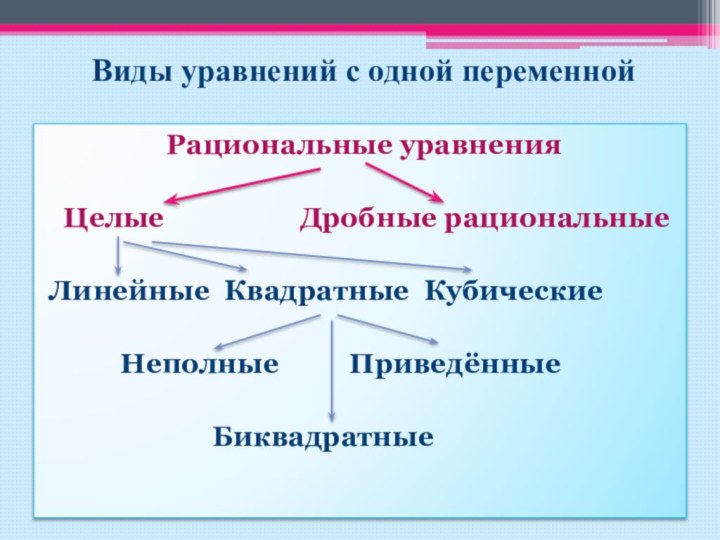
Виды уравнений с одной переменной Рациональные уравнения Целые

Дробные

рациональные

Линейные Квадратные Кубические

Неполные Приведённые

Биквадратные


Слайд 7 Определение линейного уравнения
Уравнение вида aх = b
(где

Определение линейного уравненияУравнение вида aх = b (где х – переменная,

х – переменная, а и b – некоторые числа)

называется линейным уравнением с одной переменной.


Отличительная особенность такого уравнения –
переменная х входит в уравнение обязательно в первой степени.

Слайд 8 Решите устно:
1. 14x=-7
2. 3x=0
3. |x|=8
4. |x|+9=8
5. 0x=0
6. 0x=2,3
7.

Решите устно:1. 14x=-72. 3x=03. |x|=84. |x|+9=85. 0x=06. 0x=2,37. 8. |x-6|=5 x-6=5 или x-6=-5


8. |x-6|=5
x-6=5 или x-6=-5

Слайд 9  
Корнем уравнения
6-х-3(2-5х)=12+8х
является число

  Корнем уравнения 6-х-3(2-5х)=12+8х является число

Слайд 10  
Сколько корней
имеет уравнение?
6(1,2х-0,5)-

  Сколько корней имеет уравнение? 6(1,2х-0,5)- 1,3х=5,9х -3

1,3х=5,9х -3

Слайд 11
Закончи предложение:

Формула корней квадратного уравнения…
Формула корней кв. уравнения

Закончи предложение:Формула корней квадратного уравнения…Формула корней кв. уравнения с чётным вторым

с чётным вторым коэффициентом …
Количество корней квадратного уравнения зависит

от …
Если D больше 0, то квадратное уравнение имеет … ,если D равен 0, то … , если D меньше 0, то …
Квадратные уравнения бывают …
Неполные квадратные уравнения имеют вид…
Квадратное уравнение, у которого первый коэффициент равен 1 называют …

Слайд 12 Приведённое квадратное уравнение
x2+px+q=0
Как можно

Приведённое квадратное уравнение x2+px+q=0 Как можно решить приведённое квадратное уравнение,

решить приведённое квадратное
уравнение, не используя формулу корней
квадратного

уравнения ?

Слайд 13 Теорема Виета
x2+px+q=0
x1+x2=-p

x1·x2=q
Формула разложения квадратного
трёхчлена на множители:
аx2+bx+c=a(x-x1)(x-x2)

где

Теорема Виетаx2+px+q=0x1+x2=-px1·x2=qФормула разложения квадратного трёхчлена на множители:аx2+bx+c=a(x-x1)(x-x2) где x1, x2 – корни квадратного трёхчлена

x1, x2 – корни квадратного трёхчлена

Слайд 14 «Верно-неверно»
Тест

«Верно-неверно» Тест

Слайд 15 Определите, верны ли высказывания ?
Е
Д
В
И
С
К
Р
И
М
И
В
Н
Е
А
Н
В
Т
А
Корни уравнения 2x2-32=0
являются

Определите, верны ли высказывания ?ЕДВИСКРИМИВНЕАНВТАКорни уравнения 2x2-32=0 являются противоположными числами

противоположными
числами

Слайд 16 Тест: «Верно – неверно»
Е
Д
В
И
С
К
Р
И
М
И
В
Н
Е
А
Н
В
Т
И
Один из корней уравнения

Тест: «Верно – неверно»ЕДВИСКРИМИВНЕАНВТИОдин из корней уравнения x2-x√3=0 является иррациональным числом


x2-x√3=0 является
иррациональным числом

Слайд 17 Тест: «Верно – неверно»
Е
Д
В
И
С
К
Р
И
М
И
В
Н
Е
А
Н
В
Т
К
Корнями уравнения
x2-100x+99=0
являются

Тест: «Верно – неверно»ЕДВИСКРИМИВНЕАНВТККорнями уравнения x2-100x+99=0 являются числа 1и 99

числа 1и 99

Слайд 18 Тест: «Верно – неверно»
Е
Д
В
И
С
К
Р
И
М
И
В
Н
Е
А
Н
В
Т
С
Уравнение
x2-6x+1-√2=0
имеет два

Тест: «Верно – неверно»ЕДВИСКРИМИВНЕАНВТСУравнение x2-6x+1-√2=0 имеет два различных корня

различных корня

Слайд 19 Тест: «Верно – неверно»
Е
Д
В
И
С
К
Р
И
М
И
В
Н
Е
А
Н
В
Т
Е
Корнем уравнения
x(x-3,5)=2(x-3,5)
является число

Тест: «Верно – неверно»ЕДВИСКРИМИВНЕАНВТЕКорнем уравнения x(x-3,5)=2(x-3,5)является число -2

Слайд 20 Тест: «Верно – неверно»
Д
В
И
С
К
Р
И
М
И
В
Н
А
Н
В
Т
Н
Сумма корней уравнения

Тест: «Верно – неверно»ДВИСКРИМИВНАНВТНСумма корней уравнения x2 -4x-5=0 равна 4

x2 -4x-5=0
равна 4

Слайд 21 Тест: «Верно – неверно»
Д
В
И
С
К
Р
И
М
И
В
Н
А
Н
В
Т
М
Уравнение

Тест: «Верно – неверно»ДВИСКРИМИВНАНВТМУравнение x2 -10x+25=0 имеет один корень

x2 -10x+25=0
имеет один корень

Слайд 22 Тест: «Верно – неверно»
Д
В
И
С
К
Р
И
М
И
В
Н
А
Н
В
Т
Р
Числа x1 и x2

Тест: «Верно – неверно»ДВИСКРИМИВНАНВТРЧисла x1 и x2 ,изображенные на координатной прямой,

,изображенные на
координатной прямой, являются
корнями уравнения x2

+3x-4=0

│

│

│

│

│

│

│

│

│

│

│

3

4

x1

x2

Слайд 23 Тест: «Верно – неверно»
Д
В
И
С
К
Р
И
М
И
В
Н
А
Н
В
Т
В
Уравнение 4x2 +25=0

Тест: «Верно – неверно»ДВИСКРИМИВНАНВТВУравнение 4x2 +25=0 имеет два корня


имеет два корня

Слайд 24 Физкультминутка Посчитай до десяти.

Физкультминутка Посчитай до десяти.

Слайд 25 Будь внимателен!
Что пропало?

Будь внимателен!Что пропало?

Слайд 26 у=2х; х=3 ; у=4; х=-5;

у=2х; х=3 ; у=4; х=-5; у=-8; у=-7х. Повторим с помощью

у=-8; у=-7х.
Повторим с помощью

физкультминутки,как строится график линейной функции.
Если график параллелен оси ОХ - разводим руки в стороны;
Проходит через начало координат - руки на пояс;
параллелен оси ОУ-одна рука вверх, другая-вниз.

Слайд 27  Алгоритм решения уравнений графическим способом
Из уравнения выделяем знакомые нам функции.
Строим графики

 Алгоритм решения уравнений графическим способомИз уравнения выделяем знакомые нам функции.Строим графики функций в одной

функций в одной координатной плоскости.
Находим координаты точек пересечения графиков.
Из найденных координат

выбираем значение абсциссы, т.е. х.
Записываем ответ

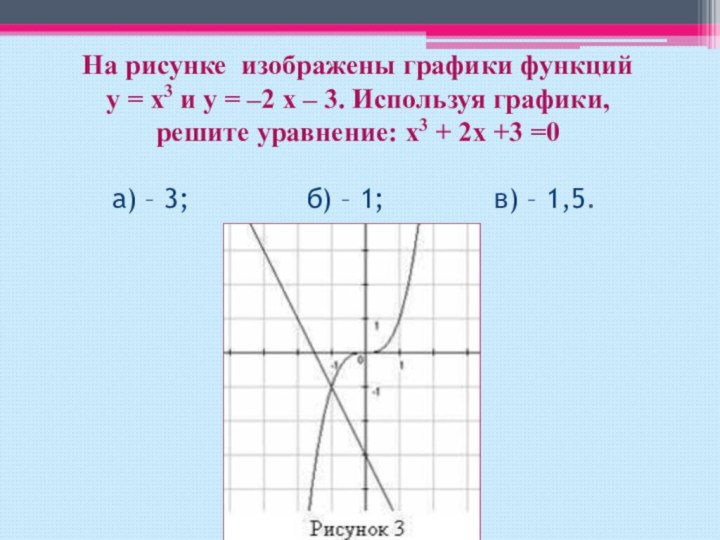
Слайд 28  На рисунке изображены графики функций у = х3 и

 На рисунке изображены графики функций у = х3 и у = –2

у = –2 х – 3. Используя графики, решите

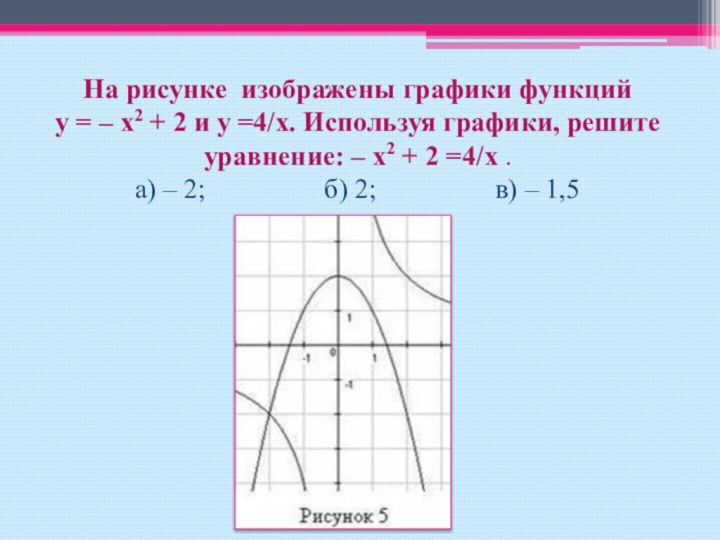
уравнение: х3 + 2х +3 =0 а) – 3;              б) – 1;             в) – 1,5.

Слайд 29 На рисунке изображены графики функций у = –

На рисунке изображены графики функций у = – х2 + 2 и

х2 + 2 и у =4/х. Используя графики, решите уравнение:

– х2 + 2 =4/х . а) – 2;                 б) 2;                 в) – 1,5

Слайд 30 Уравнение вида ах⁴+bх²+с=0,
где а, b и

Уравнение вида ах⁴+bх²+с=0, где а, b и с –данные числа

с –данные числа и а≠0,
а х - неизвестное,

называют
биквадратным уравнением.

х² = t

at²+bt+c=0

Слайд 31 Алгоритм решения биквадратного уравнения
Делаем замену переменной
Составляем и

Алгоритм решения биквадратного уравненияДелаем замену переменной Составляем и решаем квадратное уравнение

решаем квадратное уравнение с новой переменной
Делаем обратную замену и

решаем получившиеся квадратные уравнения
Делаем вывод о числе корней биквадратного уравнения
Записываем ответ

Слайд 32 Решите биквадратное уравнение
Вариант 1

Решите биквадратное уравнение Вариант 1 Вариант 2

Вариант 2

Слайд 33 Определение
Дробным рациональным уравнением называют уравнение, обе части которого

Определение Дробным рациональным уравнением называют уравнение, обе части которого являются рациональными выражениями,

являются рациональными выражениями, причём хотя бы одно из них

– дробным выражением.

Слайд 34 Решите дробно – рациональные уравнения

Нет корней

y=-5

y=-15

Решите дробно – рациональные уравненияНет корнейy=-5y=-15

Слайд 35
- найти общий знаменатель дробей, входящих в

- найти общий знаменатель дробей, входящих в уравнение;- умножить

уравнение;
- умножить обе части уравнения на

общий знаменатель;
- решить получившееся целое уравнение;
- исключить из его корней те, которые обращают в нуль общий знаменатель.

Алгоритм решения дробно-рационального уравнения:

Слайд 36 Решите уравнение:

Решите уравнение:

Слайд 37 Самостоятельная работа

Самостоятельная работа

Слайд 38 Проверь себя:

Проверь себя: Линейные: 1)

Линейные:

1) х=-1
2) х=17
3) х=-0,22

Слайд 39 Проверь себя:

Проверь себя: Квадратные: 1) х=3;х=-3

Квадратные: 1)

х=3;х=-3
2) х=-1;х=9
Кубическое: 3) х=0;х=-2;х=1

Слайд 40 Проверь себя:

Проверь себя: Дробно-рациональные: 1) х=-1,2; 1

Дробно-рациональные: 1) х=-1,2; 1

2) х=-5
3) х=1

Слайд 41 Домашнее задание:

Вариант 1-15 №9

Домашнее задание:Вариант 1-15 №9

Слайд 42 На сегодняшнем уроке:

-"Особенно мне понравилось…";
-"Сегодня

На сегодняшнем уроке: -

мне удалось…";
-"Я сумел…";
-"Было интересно…";
-"Было трудно…";
-"Я понял, что…";
-"Теперь я могу…";
-"Я

научился…";
-"Меня удивило…»
  • Имя файла: prezentatsiya-k-uroku-obobshchenie-i-sistematizatsiya-znaniy-po-teme-reshenie-uravneniy-v-9-klasse.pptx
  • Количество просмотров: 222
  • Количество скачиваний: 4
- Предыдущая Презентация открытого урока Средневековый город
Следующая - Зерно и продукты его переработки, выполнила студентка гр. 633 Фаустова Оксана

Похожие презентации

Преобразование рациональных выражений ( 9 класс) Преобразование рациональных выражений ( 9 класс) 186
Буквенная запись свойств сложения и вычитания. Буквенная запись свойств сложения и вычитания. 173
Презентация к уроку: Логарифмическая функция Презентация к уроку: Логарифмическая функция 190
Своя игра по математике 11 класс Своя игра по математике 11 класс 237
Презентация к уроку алгебры в 7 классе. График функции Презентация к уроку алгебры в 7 классе. График функции 170
Презентация по алгебре Арифметикалық прогрессия (9 класс) Презентация по алгебре Арифметикалық прогрессия (9 класс) 170
Квадратный трехчлен Квадратный трехчлен 156
Квадратичная функция 9 класс Квадратичная функция 9 класс 194
Презентация по теме Логарифмическая функция Презентация по теме Логарифмическая функция 180
Решение дробных рациональных уравнений Решение дробных рациональных уравнений 143
Устройство компьютера Устройство компьютера 199
Производная, ее геометрический и физический смысл. Правило дифференцирования сложной функции. Дифференцирование функций. Производные обратной функции и композиции функции. Использования производной для нахождения наилучшего решения в прикладных задачах. Производная, ее геометрический и физический смысл. Правило дифференцирования сложной функции. Дифференцирование функций. Производные обратной функции и композиции функции. Использования производной для нахождения наилучшего решения в прикладных задачах. 165
Презентация по математики Туынды тақырыбына есептер шығару Презентация по математики Туынды тақырыбына есептер шығару 204
Презентация по математике на тему Лидер 21 века Презентация по математике на тему Лидер 21 века 187
Квадратный корень. Арифметический квадратный корень Квадратный корень. Арифметический квадратный корень 119
Решение квадратных уравнений по формуле Решение квадратных уравнений по формуле 151
Показательные уравнения Показательные уравнения 186
Презентация Презентация 153
Презентация: Элективный курс Математика для поступающих во ВТУзы Презентация: Элективный курс Математика для поступающих во ВТУзы 137
Неопределенный интеграл Неопределенный интеграл 140
Первый урок алгебры в 7 классе Первый урок алгебры в 7 классе 201
Презентация к уроку алгебры по теме Преобразование выражений, содержащих квадратные корни Презентация к уроку алгебры по теме Преобразование выражений, содержащих квадратные корни 133
Использование производной для исследования функции и построения графика функции (10 класс) Использование производной для исследования функции и построения графика функции (10 класс) 188
Презентация по математике викторина Своя игра Презентация по математике викторина Своя игра 186
Арифметическая и геометрическая прогрессии Повторение Арифметическая и геометрическая прогрессии Повторение 81
Алгебра высказываний. Основные операции алгебры высказываний Алгебра высказываний. Основные операции алгебры высказываний 152
Презентация по теме : Прямая пропорциональность.Урок алгебры в 7 классе Презентация по теме : Прямая пропорциональность.Урок алгебры в 7 классе 156
Урок решения логарифмических неравенств Урок решения логарифмических неравенств 152
Решение систем уравнений-9класс Решение систем уравнений-9класс 173
Дробные выражения (6 класс) Дробные выражения (6 класс) 154