Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Показательная функция

Содержание

СодержаниеПоказательная функцияПоказательные уравненияПоказательные неравенстваТиповые задачиТестыДомашняя контрольная работа
Методическая разработка темы: «Показательная функция» СодержаниеПоказательная функцияПоказательные уравненияПоказательные неравенстваТиповые задачиТестыДомашняя контрольная работа Показательная функцияГрафик.ОпределениеСвойстваСодержание ОпределениеПоказательная функция – это функция вида Свойства показательной функции Область определения: все действительные числа Множество значений: График показательной функцииТ.к. , то график Показательные уравненияОпределениеПростейшие уравненияСпособы решения сложных уравненийСодержание Определение Уравнение, в котором переменная содержится в показателе степени, называется показательным. Примеры:⮍ к теме Простейшее показательное уравнение – это уравнение вида Простейшее показательное уравнение решается с Способы решения сложных показательных уравнений.Вынесение за скобки степени с меньшим показателемЗамена переменнойДеление Вынесение за скобки степени с меньшим показателемДанный способ используется, если соблюдаются два Замена переменнойПри данном способе показательное уравнение сводится к квадратному.Способ замены переменной используют, Деление на показательную функциюДанный способ используется, если основания степеней разные.а) в уравнении Показательные неравенстваОпределениеПростейшие неравенстваРешение неравенствСодержание Определение Показательные неравенства – это неравенства, в которых неизвестное Простейшие показательные неравенства – это неравенства вида:где a > 0, a ≠ При решении простейших неравенств используют свойства возрастания или убывания показательной Типовые задачи Показательная функцияПоказательные уравненияПоказательные неравенстваСодержание Показательная функция Построение графикаСравнение чисел с использованием свойств показательной функцииСравнение числа с Задача 1 Построить график функции y = 2xxy-1 87654321 - 3 Задача 2 Сравнить числа РешениеОтвет: ? списку задач Задача 3 Сравнить число с 1. Решение-5 < 0Ответ: ? списку задач Задача 4 Cравнить число р с 1 р =2 > Показательные уравнения Простейшие показательные уравненияУравнения, решаемые вынесением за скобки степени с меньшим Простейшие показательные уравненияОтвет: - 5,5.Ответ: 0; 3.? списку задач Вынесение за скобки степени с меньшим показателемОтвет: 5x + 1 - (x Замена переменной (сл.1)основания степеней одинаковы, показатель одной из степеней в 2 раза Замена переменной (сл. 2)Основания степеней одинаковы, коэффициенты перед переменной противоположны. По т. Деление на показательную функциюОтвет: 0? списку задач⮍ к теории Деление на показательную функциюОтвет: 0; 1.? списку задач⮍ к теории Простейшие показательные неравенстваДвойные неравенстваНеравенства, решаемые вынесением за скобки степени с меньшим показателемНеравенства, Простейшие показательные неравенства? списку задач Двойные неравенстваОтвет: (- 4; -1).3 > 1, то? списку задач Решение показательных неравенствМетод: Вынесение за скобки степени с меньшим Решение показательных неравенствМетод: Замена переменнойОтвет: х < -1.3>1, то? списку задач Тесты по темам: Показательная функция и её свойстваПоказательные уравненияПоказательные неравенстваСодержание Литература1). Ш. А. Алимов. Алгебра и начала анализа: Учеб. Для 10-11 кл.
Слайды презентации

Слайд 2 Содержание
Показательная функция
Показательные уравнения
Показательные неравенства
Типовые задачи
Тесты
Домашняя контрольная работа

СодержаниеПоказательная функцияПоказательные уравненияПоказательные неравенстваТиповые задачиТестыДомашняя контрольная работа

Слайд 3 Показательная функция
График.
Определение
Свойства
Содержание

Показательная функцияГрафик.ОпределениеСвойстваСодержание

Слайд 4
Определение



Показательная функция – это функция вида

ОпределениеПоказательная функция – это функция вида ,

,
где

x – переменная,
- заданное число, >0, ≠1.

Примеры:

⮍ к теме

Слайд 5 Свойства показательной функции
Область определения: все действительные числа

Свойства показательной функции Область определения: все действительные числа Множество значений: все


Множество значений: все положительные числа
При >

1 функция возрастающая; при 0 < < 1 функция убывающая.


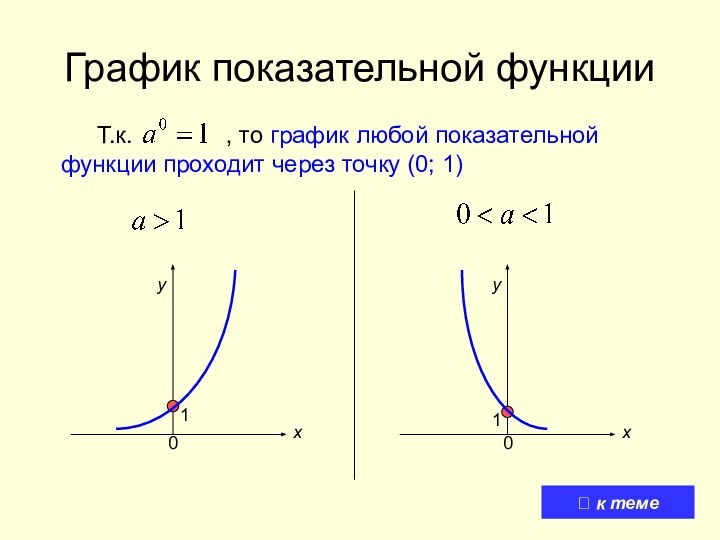
D(y) = R;

E(y) = (0; + ∞);

⮍ к теме

Слайд 6 График показательной функции
Т.к.

График показательной функцииТ.к. , то график любой показательной

, то график любой показательной функции проходит через

точку (0; 1)

1

1

х

х

у

у





0

0

⮍ к теме

Слайд 7 Показательные уравнения
Определение
Простейшие уравнения
Способы решения сложных уравнений
Содержание

Показательные уравненияОпределениеПростейшие уравненияСпособы решения сложных уравненийСодержание

Слайд 8 Определение
Уравнение, в котором переменная содержится в

Определение Уравнение, в котором переменная содержится в показателе степени, называется показательным. Примеры:⮍ к теме

показателе степени, называется показательным.
Примеры:
⮍ к теме

Слайд 9
Простейшее показательное уравнение – это уравнение вида

Простейшее

Простейшее показательное уравнение – это уравнение вида Простейшее показательное уравнение решается

показательное уравнение решается с использованием свойств степени.
⮍ к теме

Слайд 10 Способы решения сложных показательных уравнений.
Вынесение за скобки степени

Способы решения сложных показательных уравнений.Вынесение за скобки степени с меньшим показателемЗамена

с меньшим показателем
Замена переменной
Деление на показательную функцию
⮍ к теме

Слайд 11 Вынесение за скобки степени с меньшим показателем

Данный способ

Вынесение за скобки степени с меньшим показателемДанный способ используется, если соблюдаются

используется, если соблюдаются два условия:





1) основания степеней

одинаковы;
2) коэффициенты перед
переменной одинаковы

Например:


решение

Слайд 12 Замена переменной

При данном способе показательное уравнение сводится к

Замена переменнойПри данном способе показательное уравнение сводится к квадратному.Способ замены переменной

квадратному.
Способ замены переменной используют, если
показатель одной из степеней в

2 раза больше, чем
у другой.
Например:
3 2x – 4 · 3 х – 45 = 0

коэффициенты перед
переменной противоположны.
Например:
2 2 - х – 2 х – 1 =1

б)

а) основания степеней одинаковы;

решение

решение


Слайд 13 Деление на показательную функцию
Данный способ используется, если основания

Деление на показательную функциюДанный способ используется, если основания степеней разные.а) в

степеней разные.
а) в уравнении вида ax = bx делим

на bx
Например: 2х = 5х | : 5x

б) в уравнении A a2x + B (ab)x + C b2x = 0
делим на b2x.
Например:
3⋅25х - 8⋅15х + 5⋅9х = 0 | : 9x

решение

решение


Слайд 14 Показательные неравенства
Определение
Простейшие неравенства
Решение неравенств
Содержание

Показательные неравенстваОпределениеПростейшие неравенстваРешение неравенствСодержание

Слайд 15 Определение
Показательные неравенства – это неравенства,

Определение Показательные неравенства – это неравенства, в которых неизвестное содержится в показателе степени.Примеры:⮍ к теме

в которых неизвестное содержится в показателе степени.
Примеры:
⮍ к теме

Слайд 16
Простейшие показательные неравенства – это неравенства вида:




где a

Простейшие показательные неравенства – это неравенства вида:где a > 0, a

> 0, a ≠ 1, b – любое число.
⮍

к теме

Слайд 17







При решении простейших неравенств используют свойства

При решении простейших неравенств используют свойства возрастания или убывания показательной

возрастания или убывания показательной функции.




Для решения более

сложных показательных неравенств используются те же способы, что и при решении показательных уравнений.

⮍ к теме

Слайд 18 Типовые задачи
Показательная функция
Показательные уравнения
Показательные неравенства

Содержание

Типовые задачи Показательная функцияПоказательные уравненияПоказательные неравенстваСодержание

Слайд 19
Показательная функция
Построение графика
Сравнение чисел с использованием свойств

Показательная функция Построение графикаСравнение чисел с использованием свойств показательной функцииСравнение числа

показательной функции
Сравнение числа с 1

а) аналитический способ;
б) графический способ.


? типовые задачи

Слайд 20
Задача 1 Построить график функции y = 2x
x
y
-1

Задача 1 Построить график функции y = 2xxy-1 87654321 - 3



8

7

6

5

4

3

2

1
- 3 - 2 -1

0 1 2 3

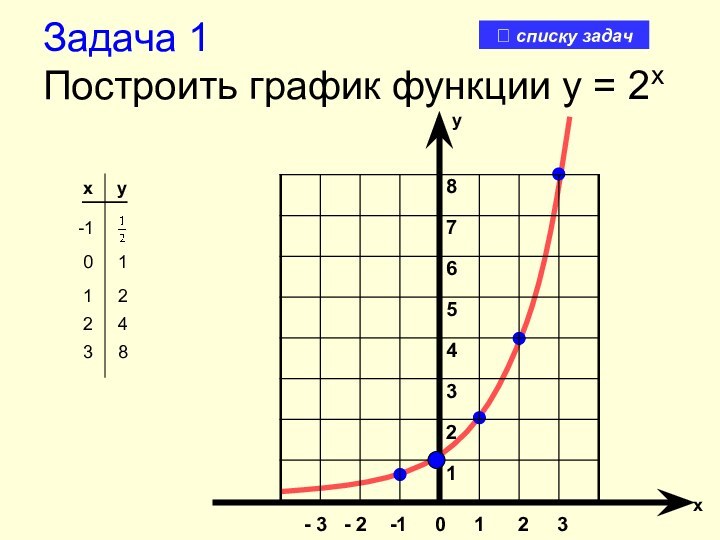
х

у





3 8

2 4

1 2

0 1


? списку задач

Слайд 21

Задача 2 Сравнить числа

Решение

Ответ:
? списку задач

Задача 2 Сравнить числа РешениеОтвет: ? списку задач

Слайд 22

Задача 3 Сравнить число с 1.
Решение
-5

Задача 3 Сравнить число с 1. Решение-5 < 0Ответ: ? списку задач

< 0


Ответ:
? списку задач

Слайд 23 Задача 4 Cравнить число р с 1

Задача 4 Cравнить число р с 1 р =2 >


р =
2 > 1, то функция у = 2t

– возрастающая.

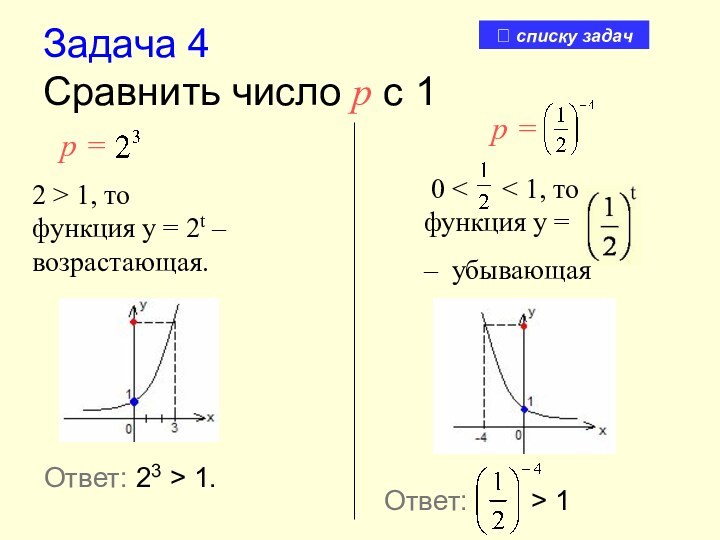
0 < < 1, то функция у =
– убывающая

Ответ: 23 > 1.

Ответ:

> 1

? списку задач

р =

Слайд 24 Показательные уравнения
Простейшие показательные уравнения
Уравнения, решаемые вынесением за

Показательные уравнения Простейшие показательные уравненияУравнения, решаемые вынесением за скобки степени с

скобки степени с меньшим показателем
Уравнения, решаемые заменой переменной

случай 1;
случай 2.
Уравнения, решаемые делением на показательную функцию случай 1;
случай 2.







? типовые задачи

Слайд 25

Простейшие показательные уравнения
Ответ: - 5,5.

Ответ: 0; 3.
? списку

Простейшие показательные уравненияОтвет: - 5,5.Ответ: 0; 3.? списку задач

задач

Слайд 26
Вынесение за скобки степени с меньшим показателем

Ответ: 5
x

Вынесение за скобки степени с меньшим показателемОтвет: 5x + 1 -

+ 1 - (x - 2) =
= x +

1 – x + 2 = 3

? списку задач

⮍ к теории

Слайд 27
Замена переменной (сл.1)
основания степеней одинаковы, показатель одной из

Замена переменной (сл.1)основания степеней одинаковы, показатель одной из степеней в 2

степеней в 2 раза больше, чем у другой .
3

2x – 4 · 3 х – 45 = 0


t = 3x (t > 0)

t 2 – 4t – 45 = 0
По т. Виета: t1· t 2 = - 45; t1+ t 2 =4

t1 = 9; t 2 = - 5 – посторонний корень


3x = 9; 3x = 32; x = 2.

Ответ: 2

? списку задач

⮍ к теории

Слайд 28
Замена переменной (сл. 2)
Основания степеней одинаковы,
коэффициенты перед

Замена переменной (сл. 2)Основания степеней одинаковы, коэффициенты перед переменной противоположны. По

переменной противоположны.
По т. Виета:

- посторонний корень
Ответ: 1
? списку задач
⮍

к теории

Слайд 29
Деление на показательную функцию
Ответ: 0
? списку задач
⮍ к

Деление на показательную функциюОтвет: 0? списку задач⮍ к теории

теории

Слайд 30
Деление на показательную функцию
Ответ: 0; 1.
? списку задач
⮍

Деление на показательную функциюОтвет: 0; 1.? списку задач⮍ к теории

к теории

Слайд 31 Простейшие показательные неравенства
Двойные неравенства
Неравенства, решаемые вынесением за скобки

Простейшие показательные неравенстваДвойные неравенстваНеравенства, решаемые вынесением за скобки степени с меньшим

степени с меньшим показателем
Неравенства, решаемые заменой переменной
Показательные неравенства
?

типовые задачи

Слайд 32





Простейшие показательные неравенства
? списку задач

Простейшие показательные неравенства? списку задач

Слайд 33
Двойные неравенства
Ответ: (- 4; -1).
3 > 1, то
?

Двойные неравенстваОтвет: (- 4; -1).3 > 1, то? списку задач

списку задач

Слайд 34

Решение показательных неравенств
Метод: Вынесение за скобки степени с

Решение показательных неравенствМетод: Вынесение за скобки степени с меньшим

меньшим
показателем
Ответ: х

>3

3 > 1, то

: 10

? списку задач

Слайд 35
Решение показательных неравенств
Метод: Замена переменной
Ответ: х < -1.

3>1,

Решение показательных неравенствМетод: Замена переменнойОтвет: х < -1.3>1, то? списку задач

то
? списку задач

Слайд 36 Тесты по темам:
Показательная функция и её свойства
Показательные уравнения
Показательные

Тесты по темам: Показательная функция и её свойстваПоказательные уравненияПоказательные неравенстваСодержание

неравенства
Содержание

  • Имя файла: pokazatelnaya-funktsiya.pptx
  • Количество просмотров: 79
  • Количество скачиваний: 0
- Предыдущая Презентация к уроку 107 по русскому языку на тему Разделительный ъ , 2 класс, ПНШ
Следующая - Презентация + пояснения Иван Фёдоров. Начало книгопечатания на Руси. Материал для внеклассного мероприятия ко Дню Православной книги

Похожие презентации

Деление дробей Деление дробей 158
Неравенства Неравенства 187
Презентация по математике на тему Преобразование графиков тригонометрических функций Презентация по математике на тему Преобразование графиков тригонометрических функций 194
Умножение и деление десятичных дробей на целое число. Математический тренажёр. Умножение и деление десятичных дробей на целое число. Математический тренажёр. 192
Презентация по математике для внеклассного мероприятия Математический бой. (7-8 класс) Презентация по математике для внеклассного мероприятия Математический бой. (7-8 класс) 224
Презентация по математике на тему: Классическое определение вероятности Презентация по математике на тему: Классическое определение вероятности 180
Презентация к уроку по теме Уравнение касательной к графику функции Презентация к уроку по теме Уравнение касательной к графику функции 190
Тренажёр Решу ЕГЭ: теоремы о вероятностях событий(профиль), часть 1 Тренажёр Решу ЕГЭ: теоремы о вероятностях событий(профиль), часть 1 192
Задачи по геометрии из банка заданий для ОГЭ (дидактический материал) Задачи по геометрии из банка заданий для ОГЭ (дидактический материал) 206
Презентация по математике на тему Тригонометрические функции Презентация по математике на тему Тригонометрические функции 180
Урок Многоугольники Урок Многоугольники 162
Сумма n членов Арифметической прогрессии Сумма n членов Арифметической прогрессии 160
Вынесение общего множителя за скобки 7 класс Вынесение общего множителя за скобки 7 класс 208
Введение в вычислительную математику Введение в вычислительную математику 204
Презентация Здоровьесберегающие аспекты урока Презентация Здоровьесберегающие аспекты урока 161
Координатная плоскость по алгебре (7 класс) Координатная плоскость по алгебре (7 класс) 179
Презентация по алгебре для 9 класса по теме Графики Квадратичной функции Презентация по алгебре для 9 класса по теме Графики Квадратичной функции 133
Задачи по функциональной грамотности Задачи по функциональной грамотности 214
Презентация устного счета по темеСтепень Презентация устного счета по темеСтепень 136
Презентация по теме Преобразование графиков функций Презентация по теме Преобразование графиков функций 153
Презентация по теме Поворот точки вокруг начала координат Презентация по теме Поворот точки вокруг начала координат 209
Вероятность 9 класс Вероятность 9 класс 187
Презентация урока геометрии по теме Значения синуса, косинуса и тангенса углов прямоугольного треугольника-2 Презентация урока геометрии по теме Значения синуса, косинуса и тангенса углов прямоугольного треугольника-2 77
Сложение чисел с разными знаками 6 класс Сложение чисел с разными знаками 6 класс 52
Дробные рациональные уравнения Дробные рациональные уравнения 189
Свойства линейной функции Свойства линейной функции 157
Творческая работа учащихся 7 класса Математика в моей будущей профессии. Творческая работа учащихся 7 класса Математика в моей будущей профессии. 172
Презентация к научно-исследовательской работе Его величество процент Презентация к научно-исследовательской работе Его величество процент 279
Арифметическая прогрессия 9 класс Арифметическая прогрессия 9 класс 162
Презентация к уроку алгебры в 9 классе: Свойства арифметического корня н-й степени Презентация к уроку алгебры в 9 классе: Свойства арифметического корня н-й степени 190