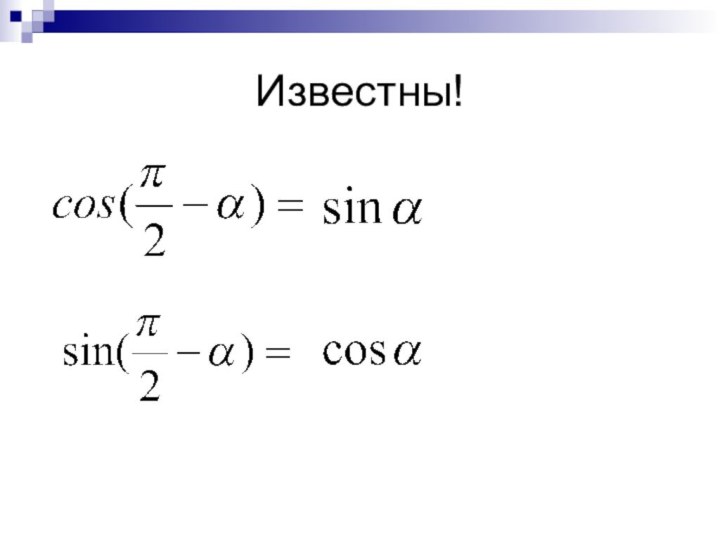Слайд 2
Цели урока:
повторить с помощью единичной окружности поведение
тригонометрических функций при изменении угла;
получить из формул сложения формулы
приведения;
ввести мнемоническое правило для более удобного запоминания формул приведения;
формировать умения и навыки учащихся в решении упражнений на применение новых знаний,
развивать у учащихся умение мыслить, наблюдательность, навыки самопроверки и объективной самооценки;
воспитывать навыки коммуникативности.
Тип урока: изучение нового материала
Оборудование и материалы для урока: проектор, интерактивная доска Interwrite, презентация для сопровождения урока, созданная в среде PowerPoint, маркерная доска
Учебник: Ю.М. Колягин, под. ред. А.Б. Жижченко. Алгебра и начала анализа. 10 кл. М.: Просвещение, 2014.
Слайд 3
Ход урока
I.Организационный момент
Проверка готовности
учащихся к уроку. Настрой учащихся на урок.
II.Актуализация опорных
знаний учащихся
2.1.Один учащийся решает у доски (маркерная) упражнение :
Вычислить с помощью формул сложения cos120˚ и sin135˚
2.2.Фронтальный опрос учащихся:
Что мы называем синусом, косинусом, тангенсом, котангенсом угла α?
На модели тригонометрического круга покажите углы 194˚, 273˚, 372˚, 278˚. Назовите четверть углов.
Назовите граничные углы в пределах от 0 до 2π
Назовите синус, косинус углов 90°, 180°, 270°
На модели тригонометрического круга покажите углы
Назовите четверть углов, знаки тригонометрических функций.
Слайд 4
На модели тригонометрического круга покажите углы и назовите
четверть, в которой располагается данный угол
1940,
1260,
3720,
2780.
вторая
третья
первая
четвертая
Назовите
граничные углы в пределах от 0 до 2π.
Чему равен sin90º,cos90º, sin π, cos π , sin270º,cos270º.
Представьте углы 1940 ,1260, 3720 , 2780 в виде суммы граничного и острого.
Слайд 5
На модели тригонометрического круга покажите углы, назовите четверть
и знаки тригонометрических функций этих углов
четвёртая
вторая
третья
третья
Слайд 6
Ход урока
2.3 Ответ учащегося у доски
2.4 Продолжение фронтального
опроса. Постановка проблемы.
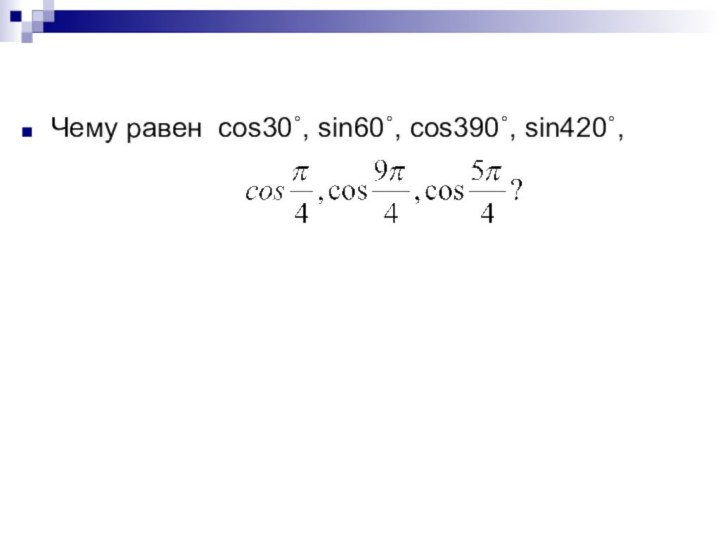
Чему равен cos30˚, sin60˚, cos390˚, sin420˚,
Как
вы считали? (представили угол в виде суммы граничного угла и острого и воспользоваться определением синуса, косинуса и формулами сложения)
Нельзя ли это сделать проще? (Надо доказать новые формулы). Как вы думаете как они называются? Почему?
Как называется тема урока?
Какие задачи урока?
Учащиеся формулируют тему урока и задачи. Записывают тему урока в тетрадь.
Слайд 7
Чему равен cos30˚, sin60˚, cos390˚, sin420˚,
Слайд 8
Формулы приведения
Цели урока:
доказать формулы приведения;
рассмотреть
примеры применения формул приведения к вычислению тригонометрических функций различных
углов
Слайд 9
Ход урока
III.Изучение нового материала
3.1 Определение
Формулируется
определение формул приведения.
3.2 Доказательство формул с помощью формул сложения
А) Две формулы доказали на предыдущих уроках
Б) Работа по группам:
доказать формулу, используя формулы сложения
Слайд 10
Определение
Формулами приведения называют формулы, позволяющие привести тригонометрические
функции аргументов
к аргументу
,
,
,
,
,
,
,
.
Слайд 12
Работа по группам:
доказать формулу, используя формулы сложения
Слайд 13
Ход урока
В) После доказательства представители групп
записывают результат на слайд. Осуществляется проверка с помощью анимации.
3.3
Вывод правила записи формул приведения
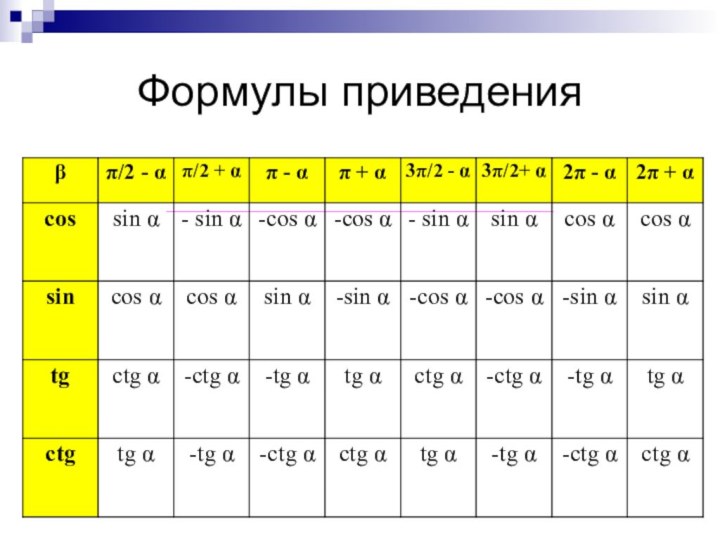
- Формулы приведения можно представить в таблице.
-Используя определение тангенса и котангенса и доказанные только что формулы можно получить ещё столько же формул приведения.
- Можно составить таблицу в 2 раза больше предыдущей.
- Легко ли все эти формулы запомнить? (нет)
- Давайте найдём закономерность.
-Учащиеся выдвигают гипотезы
- Вводится мнемоническое правило для более удобного запоминания формул приведения:
Слайд 16
Мнемоническое правило записи формулы приведения
В правой части формулы
ставится тот знак, который имеет левая часть при условии
Если в левой части формулы угол равен
, то синус заменяется на косинус, тангенс - на котангенс и наоборот.
Если угол равен , то замены не происходит.
Слайд 17
Ход урока
3.4 Известен и менее формальный
вариант этого правила – “лошадиное правило”.
Учитель формулирует
правило.
В старые добрые времена жил рассеянный математик, который при поиске ответа на вопрос 2, смотрел на свою ученую лошадь, а она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента . Если лошадь кивала головой вдоль оси Оу, то математик считал, что получен ответ “да, менять”, если вдоль оси Ох, то “нет, не менять”.
Слайд 18
«Лошадиное правило»
В старые добрые времена жил рассеянный математик,
который при поиске ответа на вопрос 2, смотрел на
свою ученую лошадь, а она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая граничному углу.
Если лошадь кивала головой вдоль оси Оу, то математик считал, что получен ответ “да, менять”,
если вдоль по оси Ох, то “нет, не менять”.
Слайд 19
Ход урока
IV.Закрепление изученного материала:
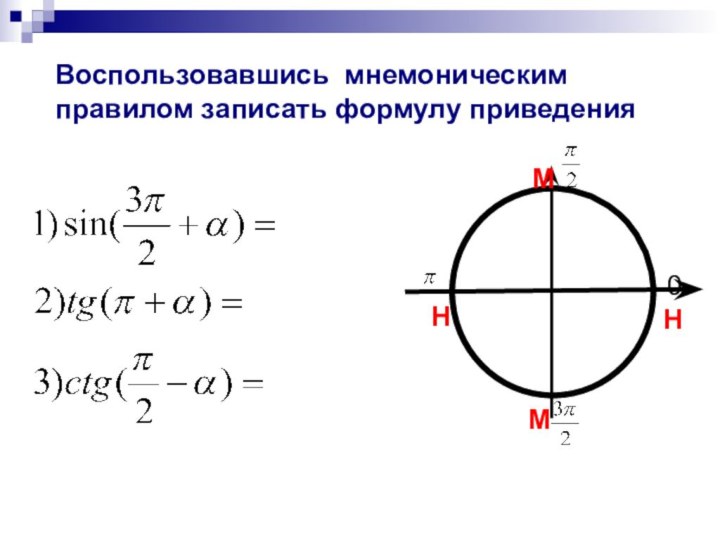
4.1 Воспользовавшись мнемоническим правилом записать
формулу приведения.
Первую формулу записывает учитель с комментированием.
Вторую записывает ученик с комментированием у доски. Третью ученик комментирует с места.
Слайд 20
Воспользовавшись мнемоническим правилом записать формулу приведения
Слайд 21
Ход урока
4.2 Где же применяются формулы приведения?
Одно из
применений – это нахождение значений тригонометрических функций различных углов.
Примеры
на вычисление:
Первый пример показывает учитель, второй и третий решают учащиеся по желанию с комментариями у доски
4.3 Самостоятельное решение упражнений
Вычислите:
Слайд 24
Ход урока
4.4. Найдите ошибку (работа в парах)
Найдите ошибки.
Составьте ключевое слово, выбрав неверные равенства.
Ключевое слово – джива
(в переводе с индийского синус). Учащимся, получившим верное слово, выставляется отметка «5», тем, у кого одна неверная буква – «4».
Слайд 25
Найдите ошибки. Составьте ключевое слово, выбрав неверные равенства
а
к
ж
о
и
в
р
д
ДЖИВА
Слайд 26
Ход урока
V. Историческая справка о понятиях «синус» и
«косинус»
Один учащийся рассказывает материал, подготовленный дома
VI.Подведение итогов урока:
Что
узнали, чему научились на уроке?
Учащиеся формулируют «мнемоническое» правило и говорят о применении формул.
VII. Домашнее задание:
выучить мнемоническое правило для формул приведения (записать в тетрадь стр. 295);
№ 154, 155 чёт (всем), 158 чёт (по желанию);
Презентация об Эйлере (по желанию).
Слайд 27
0
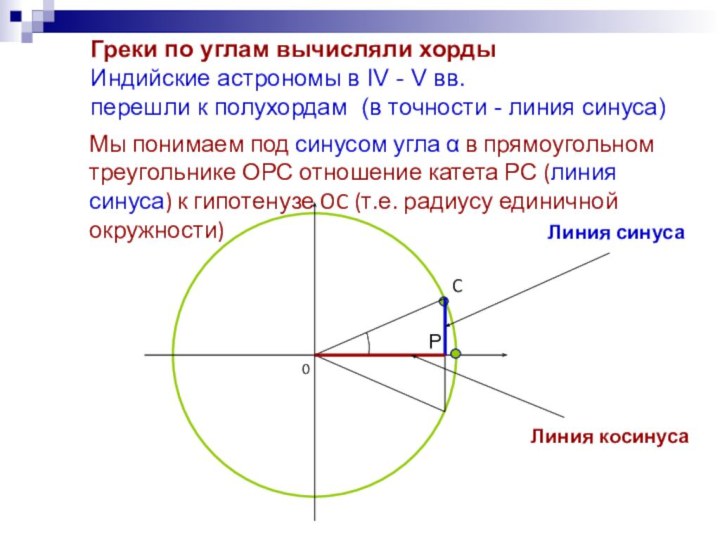
Мы понимаем под синусом угла α в прямоугольном
треугольнике ОРС отношение катета РС (линия синуса) к гипотенузе
OC (т.е. радиусу единичной окружности)
Линия синуса
Линия косинуса
Греки по углам вычисляли хорды
Индийские астрономы в IV - V вв.
перешли к полухордам (в точности - линия синуса)
Слайд 28
Термины «синус» и «косинус» пришли к нам от
индийцев.
Полухорду индийцы называли «ардхаджива» (в переводе с санскрита -
«половина тетевы лука»), а потом сократили до «джива».
Мусульманские астрономы и математики восприняли его как «джиба», а затем оно превратилось в «джайб» (на арабском - «выпуклость», «пазуха»).
Наконец в XII веке «джайб» буквально перевели на латынь словом sinus, которое не имело никакого отношения к обозначаемому им понятию.
Санкскритское «котиджива» - синус остатка(до 90º), а на латинском -sinus complementi, т.е. синус дополнения, в XVII в. сократилось до слова «косинус»