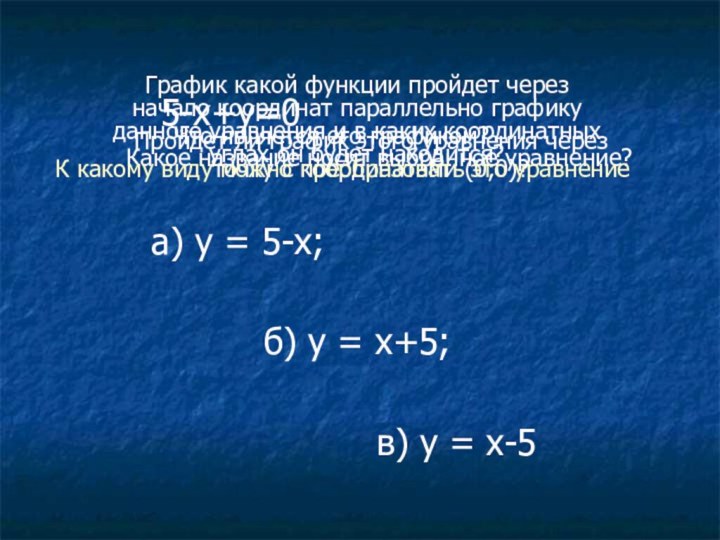Презентация на тему по Линейная функция, 7 класс

что с точки зрения моделирования реальных процессов соответствует равномерным

процессам.
МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ КОНЦЕПЦИИ ИЗУЧЕНИЯ ФУНКЦИИ
Уход от формулировки определения функции при первом появлении этого понятия
Постепенное введение в программу свойств функции, подлежащих изучению на различных уровнях строгости
Изучение функции идет в 6 направлениях:
1)графическое решение уравнений (неравенств);
2)отыскание наименьшего и наибольшего значения
функции;
3) функциональная символика;
4) кусочные функции;
6)чтение графика.

это возраст формирования мировоззрения , нравственных убеждений, принципов и

идеалов, системы оценочных суждений, которыми подросток начинает руководствоваться в своем поведении.
На развитие школьника и его поведение оказывает существенное влияние сила потребностей, мотивов, интенсивность и острота эмоциональных реакций.
В подростковом возрасте существенно перестраивается характер учебной деятельности. Подростки могут мыслить логически, заниматься теоретическими рассуждениями, самоанализом.
Они не всегда умеют управлять своим вниманием, трудности бывают с устойчивостью и с переключением внимания.
Центр жизни перемещается в сферу общения. Высокая потребность в самоутверждении, одобрении

учащихся;
Принцип реалистичности с точки зрения возможности усвоения основного содержания

раздела за 11 часов.
Принцип полноты
Принцип однотипности
Принцип контрпримеров
Принцип сравнения
Принцип непрерывного повторения
Принцип вариативности
Принцип единственного различия
Принцип инвариантность
Принцип практической направленности

ПО ИСТОЧНИКУ ПОЛУЧЕНИЯ ЗНАНИЙ
словесные
наглядные
Практические
ПО СТЕПЕНИ ВЗАИМОДЕЙСТВИЯ

УЧИТЕЛЯ И УЧАЩИХСЯ
Беседа
Самостоятельная работа
ПО ХАРАКТЕРУ ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ УЧАЩИХСЯ
Объяснительно-иллюстративный
Репродуктивный
Проблемное изложение
Частично-поисковый(или эвристический)
ФОРМА ОБУЧЕНИЯ:
урок

5.МЕТОДЫ ОБУЧЕНИЯ

как универсальном языке науке; средства моделирования явлений и процессов;

об идеях и методах математики;
Развитие логического мышления, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности;
Овладение математическими знаниями и умениями необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин;
Воспитание средствами математики культуры личности, понимания значимости математики для научно- технического прогресса, отношение к математике как к части общечеловеческой культуры через знакомство с историей развития математики;
Научить самостоятельно добывать информацию, необходимую в практической деятельности и продолжения образования.

учащиеся должны:

уметь ясно, точно, грамотно излагать свои мысли в устной и письменной речи; понимать смысл поставленной задачи; выстраивать аргументацию
владеть математическим языком
уметь распознавать логически некорректные высказывания
уметь контролировать процесс и результат математической деятельности

о модели реальной действительности
Иметь представление о математическом моделирование

как методе познания действительности
Уметь пользоваться алгоритмом и составлять план(алгоритм) выполненных действий
Уметь самостоятельно ставить цели
Уметь находить в различных источниках информацию

с двумя переменными, линейной функции
Уметь читать график функции(выявлять свойства

функции, заданной графически)
Уметь выявлять свойства функции, заданной аналитически
Уметь словесно, аналитически и графически интерпретировать взаимное расположение графиков функций, решения уравнений, неравенств
Владеть символьным языком математики
Эстетически воспринимать графики функции

координат для решения математических и прикладных задач: графическое представление

задачной ситуации в системе координат, аналитическое и графическое истолкование условия задачи, процесса и результата ее решения
Знать о различных моделях(способах) задания функции(словесной, графической, аналитической)

СИСТЕМАТИЗАЦИИ И ОБОБЩЕНИЯ ЗНАНИЙ
ЦЕЛИ:
ОРАЗОВАТЕЛЬНЫЕ:

повторить и систематизировать знания, полученные при изучении темы
«Линейная функция»; подготовиться к контрольной работе.
РАЗВИВАЮЩИЕ:
развивать навыки групповой самоорганизации и публичных выступлений; умение ясно, точно, грамотно излагать свои мысли в устной речи; выстраивать аргументацию; умение распознавать логически некорректные высказывания; умение контролировать результат математической деятельности
ВОСПИТАТЕЛЬНЫЕ:
Воспитывать уверенность в своих силах; активную жизненную позицию

1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ.(2 мин)
2. МОТИВАЦИОННО

– ОРЕНТИРОВОЧНАЯ ЧАСТЬ.
№1.
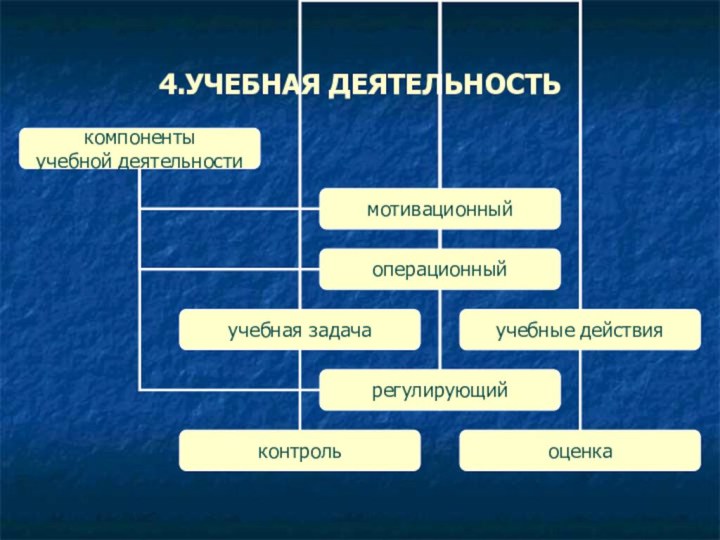
Учитель сообщает, что изучение темы «Линейная функция» подошло к концу и предлагает ребятам, работая в группах, вспомнить с какой учебной задачи началось изучение темы, ее основные понятия и последовательность их изучения. Время выполнения задания 5 мин. Результат работы записывается на доске в виде цепочки и сохраняется до окончания урока. №2.
Фронтальная, устная работа(5 мин)

систему координат;
Плоскость, на которой построена прямоугольная система координат, называется

координатной плоскостью;
Система координат разбивает координатную плоскость на четыре координатных угла;
Точка пересечения двух перпендикулярных координатных осей называется началом координат;
Точка А имеет координаты (4,2);
Ордината точки В равна -2;
Горизонтальную прямую Ох называют осью абсцисс.
Почему неверны оставшиеся утверждения?

переменными
а) 16х-2=0
б)у-2х=0
в) 5-х+у=0
г) х² - у=0
д) у -

2=0

б) у = х+5;

в) у = х-5

Какое название носит выбранное уравнение?

Что является его графиком?

Пройдет ли график этого уравнения через точку с координатами (0;0)?

График какой функции пройдет через начало координат параллельно графику данного уравнения и в каких координатных углах он будет находится?

К какому виду можно преобразовать это уравнение

а) у = -8х+2;

б) у = 4х-3;
в) у = -8х-3
назовите те, графики которых:

параллельны

пересекаются

пересекаются в точке на оси ординат

задают возрастающую функцию

задают убывающую функцию

и через 10 мин показывает его решение все ученикам

класса.

ГРУППА 1.
Постройте график функции у=2х+3 (1 способ).С помощью графика найдите наименьшее и наибольшее значение функции на[-2;1].

ГРУППА 2.
Постройте график функции у=2х+3 (2 способ).С помощью графика найдите: а) при каких значениях х график функции выше оси Ох; б) при каких значениях х выполняется неравенство 2х+3>0.

ГРУППА 3.
Выясните корректно ли задание: найти точку пересечения указанных прямых. Если задание корректно, то выполните его.
а) у = 2х и у = 2х-3; б) у=3х и у=2х-1.

5х+3у-15=0 с осями координат. Принадлежит ли точка с координатами

(3\5;4) графику этого уравнения.

ГРУППА №5.
Задайте линейную функцию, график которой параллелен прямой -4х+2у+1=0 и проходит через точку А(0;0). Назовите вид угла, который образует график полученной функции с положительной полуосью Ох.

4) РЕФЛЕКСИВНО-ОЦЕНОЧНАЯ ЧАСТЬ.(ПОДВЕДЕНИЕ ИТОГОВ)(8 мин)
(Фронтальный опрос)
Ученики отвечают на вопрос: «чем занимались сегодня на уроке?».
При этом могут использовать цепочку понятий, записанную в начале урока.

вида «закончи предложение». Каждый ученик берет и отвечает на

полученный вопрос. Опрос ведется по цепочке.
Вопросы:
Прямоугольная система координат – это…
Координатная плоскость-это…
Точка А(2,4) находится на пересечении прямых-…
Точка А(2,4) находится в … координатном угле
Точка А(-2,4) находится в … координатном угле
Точка А(-2-,4) находится в … координатном угле
Точка А(2,-4) находится в … координатном угле
Уравнение ах+ву+с=0 называется …
Уравнение ах+ву+с=0 можно привести к виду …
Уравнение у=кх+м называется …
Графиком линейной функции является …
Для построения графика линейной функции достаточно взять …
График линейной функции у=кх+м можно построить путем сдвига …
И так далее.
Учитель задает домашнее задание.(стр. 61 №3;4;5;7;8.)
Старшие групп заполняют «оценочный лист»

и др.-13-е изд., испр. - М.: Мнемозина, 2009.
Алгебра. 7

класс: методическое пособие для учителя/ А. Г. Мордкович. – М. : Мнемозина, 2008.
Алгебра. 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений / Л.А. Александрова; под ред. А.Г.Мордковича.- 5-е изд., стер. - М.: Мнемозина, 2009.
Алгебра. 7 класс. Контрольные работы для учащихся общеобразовательных учреждений / Л.А. Александрова; под ред. А.Г.Мордковича.- 3-е изд., испр. и доп.. - М.: Мнемозина, 2009.
Математические модели в курсе алгебры 7 класса: Рабочая тетрадь и тренажер по алгебре. Учебное пособие для 7 класса общеобразовательных учебных заведений/Е. Н. Перевощикова.-Н.Новгород: 2009.