Презентация на тему по математике на тему:Решение экстремальных задач

был бы виден смысл какого-нибудь максимума или минимума.

Л. Эйлер.

встречаются задачи, которые связаны с понятием НАИБОЛЬШЕГО, НАИЛУЧШЕГО, НАИБОЛЕЕ

ВЫГОДНОГО и т.д. Такие задачи получили название ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ.
Введение таких задач в обучение педагогически оправдано, т.к. они с достаточной полнотой закладывают в сознании учащихся понимание того, как человек ищет, постоянно добивается решения жизненных задач.

знакомству учеников с некоторыми идеями и прикладными методами

школьного курса математики, которые часто применяются в трудовой деятельности, в познании окружающей действительности;
формированию глубоких взглядов на процессы, происходящие как в природе, так и в повседневной жизни;
углублению и обогащению математических знаний учащихся.

Все решения экстремальных задач предлагаются на уровне исследования реальной ситуации с использованием оптимизационных средств, что особенно важно в сегодняшних условиях обучения, а также при подготовке к ЕГЭ.

перебора
Метод преобразования плоскости.

В курсе математики 5-6 классов учащимся

нередко приходится решать задачи, в которых допускается несколько или даже много решений, причем не всегда равнозначных. В таких случаях можно ставить дополнительный вопрос: найти наиболее выгодное (или достаточно выгодное по тем или иным причинам) решение, т.е. решать экстремальные задачи.
С такими задачами приходится сталкиваться при изучении следующих тем: « Меньше или больше», «Площадь. Формула площади прямоугольника», «Деление натуральных чисел». Учащимся можно специально предлагать экстремальные задачи.
При решении задач целесообразно постепенно приучать учеников 5-6 классов сводить решение задачи к решению неравенств вида ax ≤ b, где b- натуральное число.

есть 50 руб. Он собирается купить несколько тетрадей по

цене 6 руб. и линейку за 7 руб. Может ли он купить 5,7,9 тетрадей. Какое наибольшее число тетрадей он может купить?
Решение.
1)50-7=43(руб) останется на покупку тетрадей.
2)43:6=7 тетрадей(ост.1 руб)
«Метод оценки»:
1)7+6<50
2)5•6+7<50
3)7•6+7<50
4)9•6+7>50
х•6+7<50, x•6<43, x=1,2,3,4,5,6,7
Наиболее выгодным решением является х=7.

болванки 16 кг. Сколько болванок потребуется, чтобы отлить 41

деталь массой 12 кг каждая?
Решение.
1 способ: 1)12•41=492(кг)
2) 492:16=30 болванок ( 12 кг ост)
Ответ: 31 болванка Внимание! В ответе пишут часто 30 болванок!
2 способ: n- количество болванок, 16n – масса болванок, 12•41 –масса деталей. 16n≥12•41
16n≥492
n≥30 n=31,32,33,…
Наименьшее число болванок равняется 31.

представляют очень большой интерес. Решение их в 5-6 классах

методом оценки формирует первое представление о максимальном произведении при постоянной сумме двух переменных и о минимальной сумме при постоянном произведении.

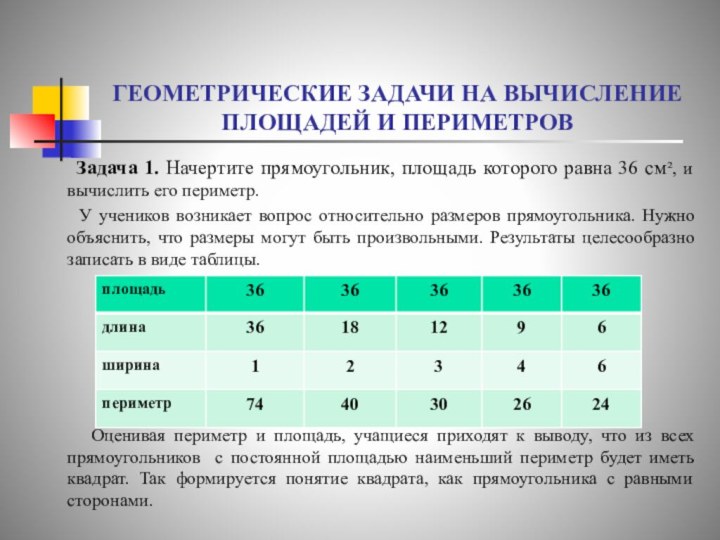
Начертите прямоугольник, площадь которого равна 36 см², и вычислить

его периметр.
У учеников возникает вопрос относительно размеров прямоугольника. Нужно объяснить, что размеры могут быть произвольными. Результаты целесообразно записать в виде таблицы.






Оценивая периметр и площадь, учащиеся приходят к выводу, что из всех прямоугольников с постоянной площадью наименьший периметр будет иметь квадрат. Так формируется понятие квадрата, как прямоугольника с равными сторонами.

2. Начертить прямоугольник, периметр которого равен 36 см, вычислить

его площадь.







Наибольшую площадь имеет квадрат.

встречаются задачи, достаточно простые, где число рассматриваемых элементов невелико.

Это создает хорошую возможность детям увидеть особенности применения метода перебора.
Задача. С помощью цифр 9 и 2 напишите все двузначные числа, в каждом из которых все цифры различны. Среди найденных чисел найдите наибольшее и наименьшее.
Задача. С помощью цифр 5,2 и 7 напишите все трехзначные числа, в каждом из которых все цифры различны. Среди найденных чисел найдите наибольшее и наименьшее.
На первый взгляд, кажется, что это очень простая задача, но она несёт большую теоретическую нагрузку. Ученики знакомятся с упорядоченными множествами, с методом перебора, перестановками, с методическими приёмами поиска экстремальной перестановки.

При изучении тем «Наибольший общий делитель»

и «Наименьшее общее кратное» используются задачи:
1)Сколько букетов можно сделать из 18 желтых и 24 красных роз, если в каждом букете должно быть наибольшее, но не во всех букетах одинаковое количество желтых и одинаковое количество красных роз?[6]
2)Для подарков детям купили 80 штук апельсинов, 240 конфет и 320 орехов. Какое наибольшее количество одинаковых подарков можно изготовить и по сколько апельсинов, конфет и орехов будет в каждом подарке? [80]
Решение таких задач способствует приобретению комбинаторных навыков, приемов и методов решения задач вообще.

Решение экстремальных задач в курсе алгебры

проходит в два этапа.
На первом этапе рассматривается неопределенная задача, текст которой переводится на математический язык в виде неопределенных уравнений (функции), которое допускает много или бесконечно много решений.
На втором этапе по тем или иным признакам определяется какое из решений задачи наиболее выгодно.

Темы курса алгебры, в которых приходится решать

экстремальные задачи:
1) «Линейная функция».
2) «Системы линейных уравнений».
3) «Рациональные дроби».
4) «Неравенства».
5) «Квадратичная функция».
6) «Последовательности. Арифметическая прогрессия».
7) «Преобразование выражений, содержащих квадратные корни».

заводами А и В по шоссейной дороге 8 км.

Где строить общежитие, в котором должны жить 500 рабочих завода А и 300 рабочих завода В, чтобы общее расстояние, которое будут проезжать все рабочие, было наименьшим?
Решение.

строительстве фермы нужно провести водопровод протяженностью 167 м. Имеются

трубы длиной 5м и 7м. Сколько нужно использовать тех и других труб, чтобы сделать наименьшее количество соединений?
Решение. Обозначим через х – количество 7-метровых труб, а через у – количество 5-метровых труб.
Получаем неопределенное уравнение 7х+5у=167
у=(167-7х):5=33-х-0,2(2х-2).
Методом перебора находим пары значений, удовлетворяющих уравнению:
(1;32), (6;25), (11;18), (16;11), (21;4). Из этих решений наиболее выгодное последнее, т.е. х=21, у=4.

Скорость течения в канале на различных глубинах выражается формулой

v(h)=-62,5h2+50h+40, где h –глубина (в м), v- скорость (в м/мин). Как меняется с глубиной погружения скорость движения воды. На какой глубине скорость течения наибольшая?

Решение.
Выделим квадрат двучлена: v(h)=-62,5h2+50h+40=-125/2(h-2/5)2+50.
Наибольшая скорость течения в канале50м/мин на глубине 0,4м.

особенностью геометрических задач на нахождение экстремумов, решаемых методом опорных

функций, является составление геометрических формул, непосредственно подсказанных соответствующими теоремами. Речь идет о таких теоремах и формулах, как теоремы косинусов, синусов; формулы для вычисления площадей; формулы метрических соотношений в прямоугольном треугольнике и др.

дм найдите тот, у которого площадь наибольшая.

Решение. 1 способ. Пусть Sплощадь прямоугольника, х и у его стороны. Тогда х2+у2=(8√2)2, т.е. х2+у2=128, у=√128-х2.

Наибольшее значение функция принимает при х=у=8 и оно равно 64.
2 способ. S=0,5(8√2)2sin=64sin
Sнаиб=64, при =90.



Из всех прямоугольников наибольшую площадь имеет квадрат с диагоналями 8√2.

Как видно из примеров, решение экстремальных задач

даёт возможность установить более тесную межпредметную связь алгебры, геометрии и физики. При их решении ученики приобретают не только математическую информацию, но и знания из курса физики. Решение физических задач поучительно с точки зрения математики, так как можно показать тонкости тех или иных математических приемов в действии, в их практическом приложении.