- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Определение тригонометрических функций
Содержание
- 2. Определение синуса и косинуса hM(x;y)αNK
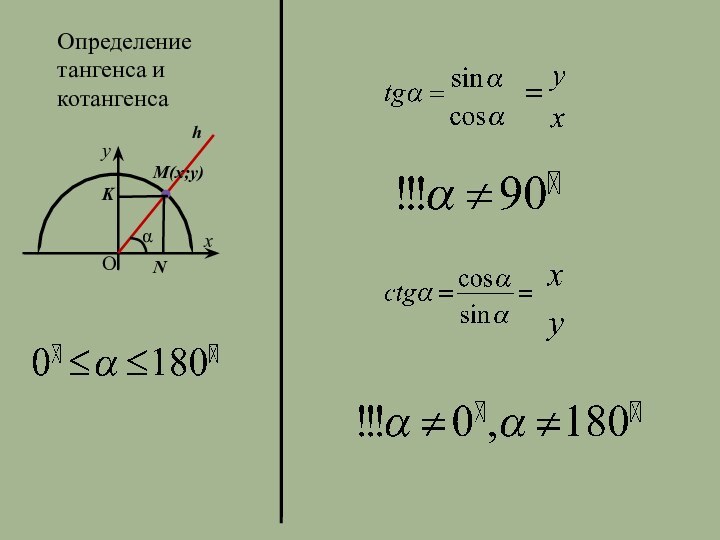
- 3. Определение тангенса и котангенса
- 4. Основное тригонометрическое тождествоyxДля любого угла α (
- 5. Таблица значений тригонометрических функций для углов 0°, 90°, 180° А(1;0)С(0;1)В(-1;0)01Не сущ0 1 0Не сущ00-10Не сущ
- 6. Практическое заданиеНачертите единичную полуокружность и постройте углы,
- 7. Практическое заданиеНачертите единичную полу-окружность и постройте углы,
- 8. Таблица значений sinα, cosα, tgα, ctgα для
- 9. Связь между тангенсом и котангенсом угла Для
- 10. Формулы приведения270°yxsin ( 90° - α )
- 11. Формулы приведения270°yxcos ( 90° - α )
- 12. Формулы приведения270°yxtg ( 90° - α )
- 13. Формулы для вычисления координат точкиА(x;y)Координаты точки А(x;
- 17. Задача.Принадлежат ли единичной окружности
- 18. Задачи по готовым чертежам (урок № 28)Найдите x, y.K
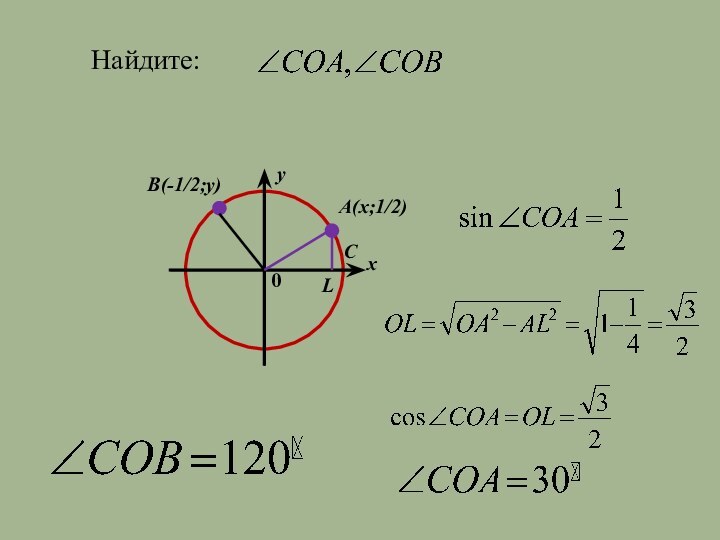
- 19. Найдите:В(-1/2;y)A(x;1/2)CL
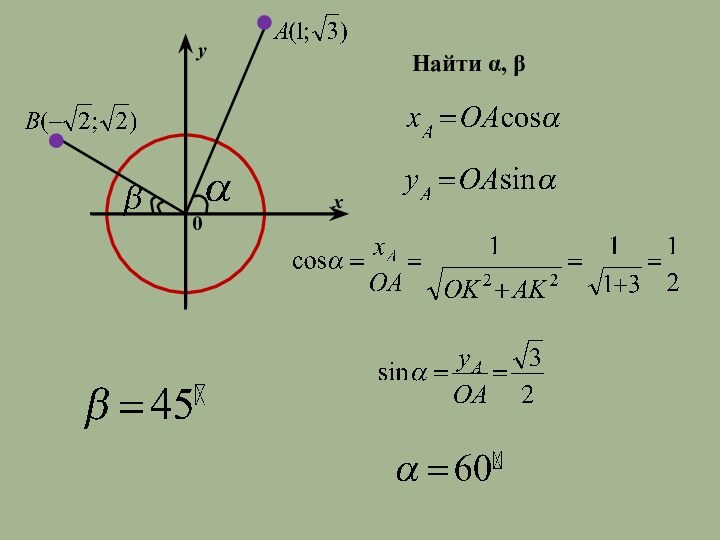
- 20. Найти α, β
- 21. Скачать презентацию
- 22. Похожие презентации









Слайд 2
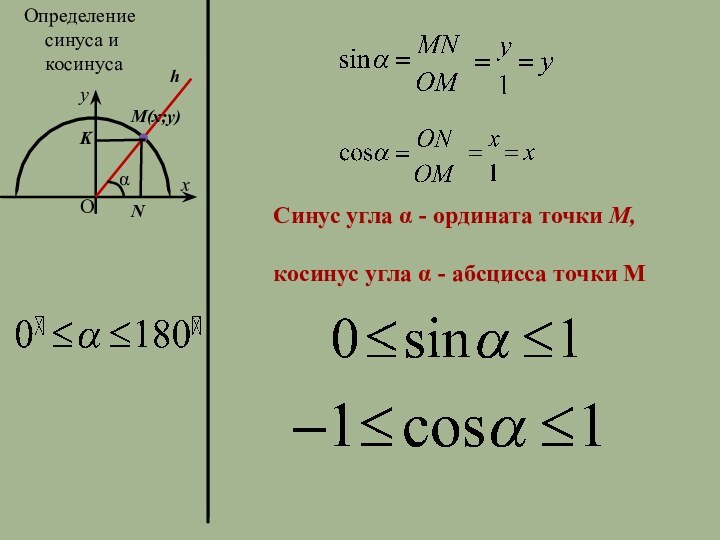
Определение синуса и косинуса
h
M(x;y)
α
N
K
Синус
угла α - ордината точки М,
угла α - абсцисса точки М
Слайд 4
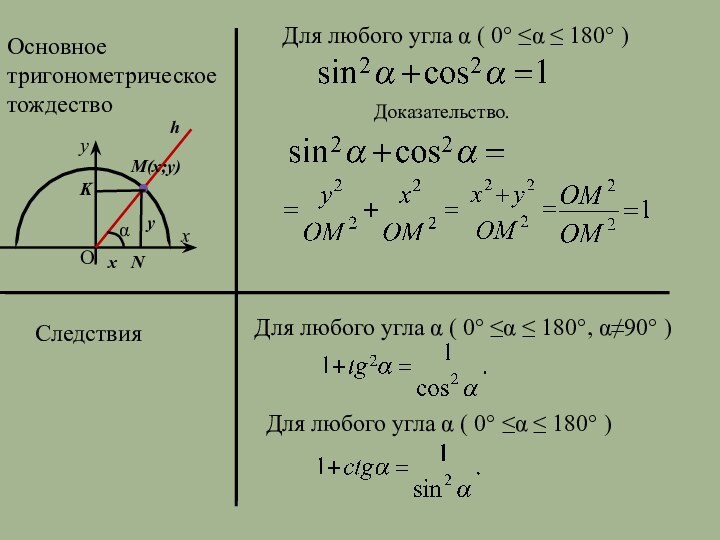
Основное тригонометрическое тождество
y
x
Для любого угла α ( 0°
≤α ≤ 180° )
Доказательство.Следствия
Для любого угла α ( 0° ≤α ≤ 180°, α≠90° )
Для любого угла α ( 0° ≤α ≤ 180° )
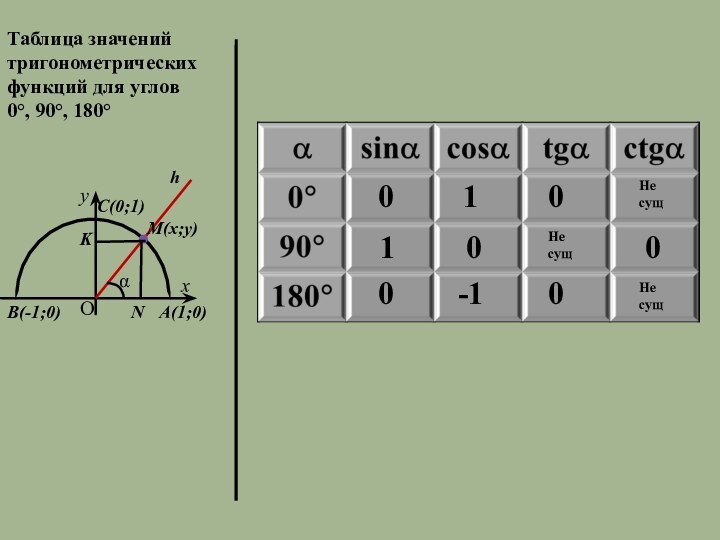
Слайд 5 Таблица значений тригонометрических функций для углов 0°, 90°,
180°
А(1;0)
С(0;1)
В(-1;0)
0
1
Не сущ
0
1
0
Не сущ
0
0
-1
0
Не сущ
Слайд 6
Практическое задание
Начертите единичную полуокружность и постройте углы, синусы
которых равны 0,3; 0,5; 0,6; 0,8; 1
Образец решения.Синус угла – это ордината точки. Необходимо знать и абсциссу точки, которая равна косинусу угла.
y=0,3,
y=0,5, x≈0,87
y=0,6, x=0,8
y=0,8, x=0,6
y=1, x=0
Слайд 7
Практическое задание
Начертите единичную полу-окружность и постройте углы, тангенсы
которых равны: 2; 1; -2; 3.
Образец решения.Построим луч ОМ так, чтобы tgα=2. Пусть точка М принадлежит единичной полуокружности и имеет координаты (x;y). Тогда sinα=y, cosα=x, поэтому tgα=y/x=2, y=2x.
Таким образом, задача сводится к построению точки М единичной полуокружностиx с координатами (x;y), удовлетворяющими условию y=2x
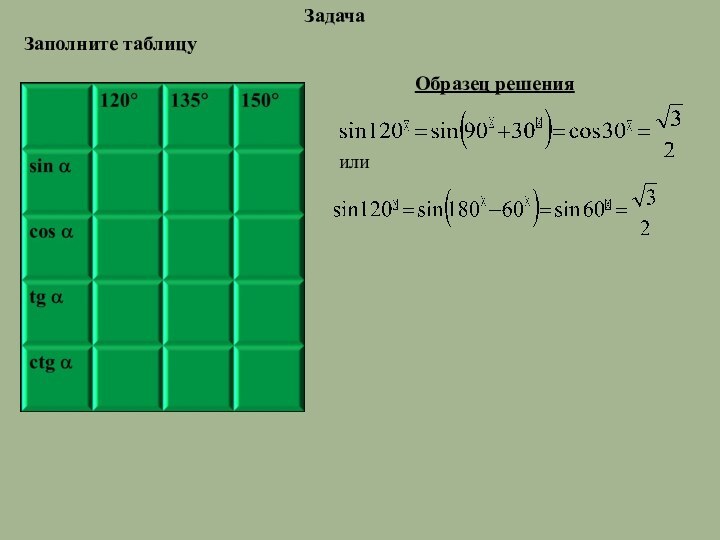
Слайд 8
Таблица значений sinα, cosα, tgα, ctgα
для углов
α, равных 30°, 45°, 60°, 90°, 180°, 270°.
0
1
-1
0
-1
0
1
Не
сущ0
Не сущ
1
0
Не сущ
0
Слайд 9
Связь между тангенсом и котангенсом угла
Для любого
угла α ( 0° ≤α ≤ 180°, α≠90° )
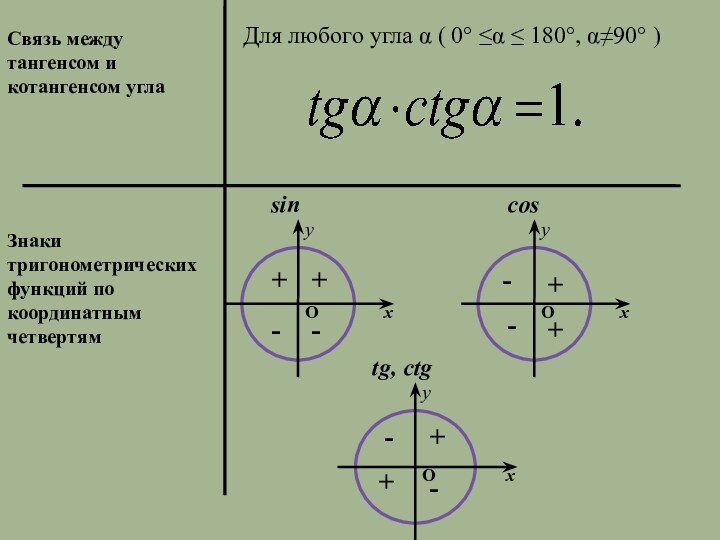
Знаки
тригонометрических функций по координатным четвертям+
+
-
-
+
+
-
-
+
-
+
-
Слайд 10
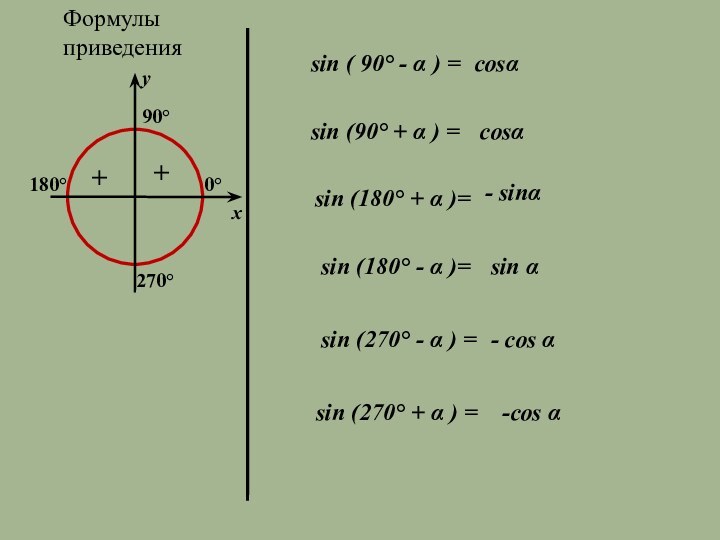
Формулы приведения
270°
y
x
sin ( 90° - α ) =
cosα
sin
(90° + α ) =
cosα
sin (180° + α
)= - sinα
sin (180° - α )=
sin α
sin (270° - α ) =
- cos α
sin (270° + α ) =
-cos α
+
+
Слайд 11
Формулы приведения
270°
y
x
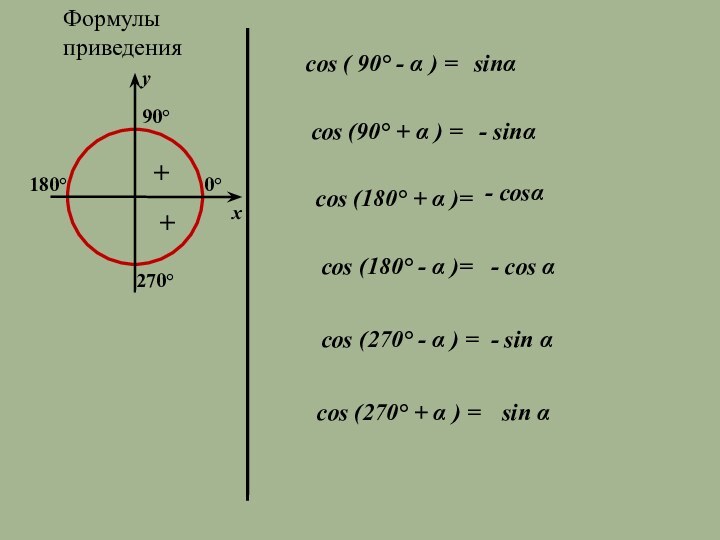
cos ( 90° - α ) =
sinα
cos
(90° + α ) =
- sinα
cos (180° +
α )= - cosα
cos (180° - α )=
- cos α
cos (270° - α ) =
- sin α
cos (270° + α ) =
sin α
+
+
Слайд 12
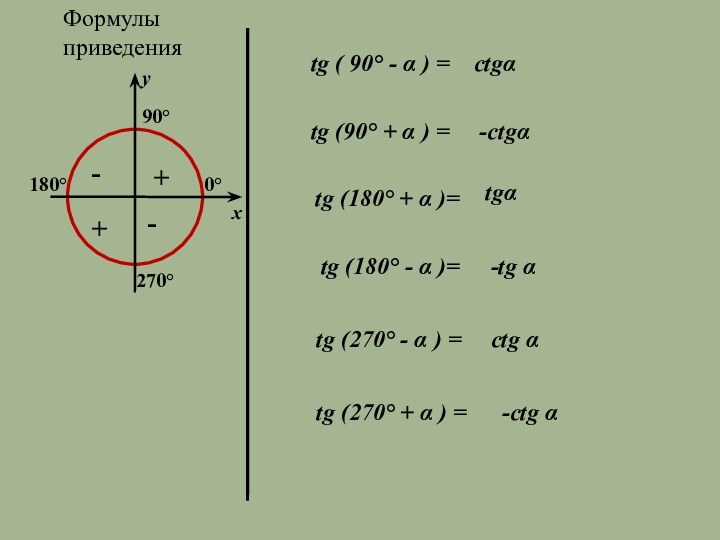
Формулы приведения
270°
y
x
tg ( 90° - α ) =
ctgα
tg
(90° + α ) =
-ctgα
tg (180° + α
)= tgα
tg (180° - α )=
-tg α
tg (270° - α ) =
ctg α
tg (270° + α ) =
-ctg α
+
-
+
-
Слайд 13
Формулы для вычисления координат точки
А(x;y)
Координаты точки А(x; y)
определяются по формулам
x = OA cos α ;
y = OA sin α M
(cosα;sinα)
Слайд 14
Задача.
Найдите значения косинуса, тангенса, котангенса угла α,
если sinα=0,6, 90°<α<180°sin2α + cos2α =1
Слайд 16
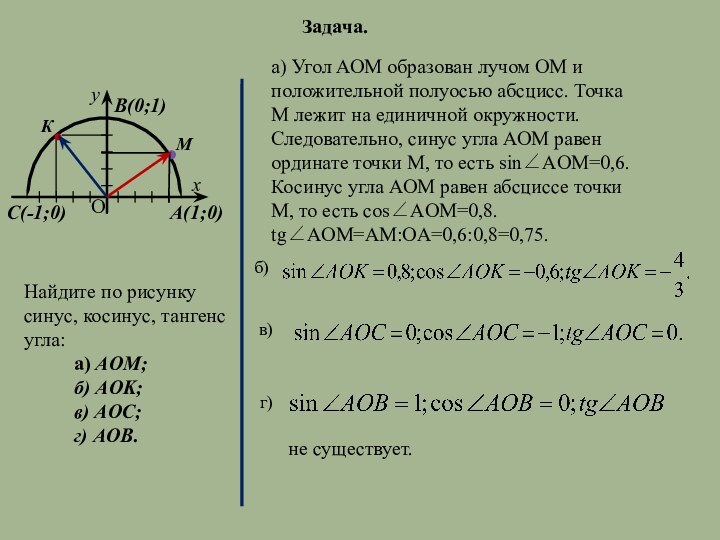
Задача.
M
В(0;1)
А(1;0)
С(-1;0)
КНайдите по рисунку синус, косинус, тангенс угла:
а) AOM;
б) AOK;
в) AOC;
г) AOB.
а) Угол АОМ образован лучом ОМ и положительной полуосью абсцисс. Точка М лежит на единичной окружности. Следовательно, синус угла АОМ равен ординате точки М, то есть sin∠AOM=0,6. Косинус угла АОМ равен абсциссе точки М, то есть cos∠AOM=0,8.
tg∠AOM=AM:OA=0,6:0,8=0,75.
б)
в)
г)
не существует.
Слайд 17
Задача.
Принадлежат ли единичной окружности точки:
а)
Р(-0,6; 0,8);
б) Т ;
в) H
?
Точка с координатами ( x; y) принадлежит единичной окружности, если выполнены два условия: 1) -1≤ x ≤ 1, -1≤ y ≤ 1; 2) x2+y2=1.
а) Координаты точки Р удовлетворяют первому условию, так как : -1≤ -0,6 ≤ 1, -1 ≤ 0,8 ≤ 1.
Проверим второе условие : x 2+ y 2 = =0,36 + 0,64 = 1, следовательно, выполняется второе условие. Поэтому точка Р принадлежит единичной окружности.
Ответы:
б) не принадлежит;
в) принадлежит
Образец решения