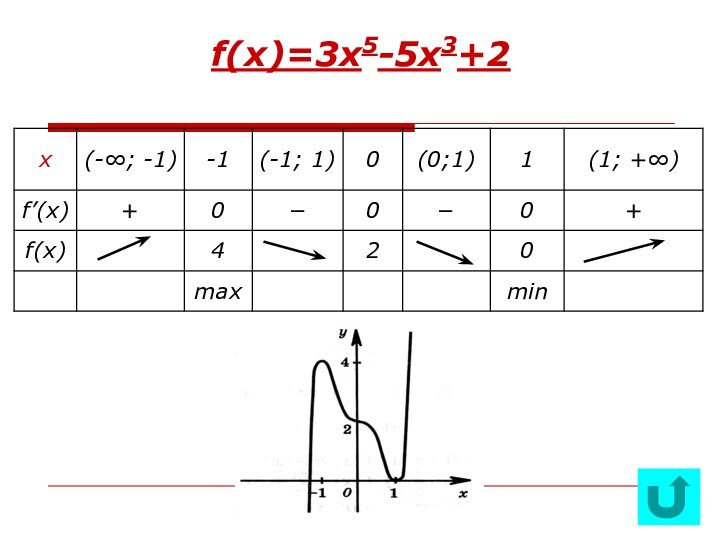
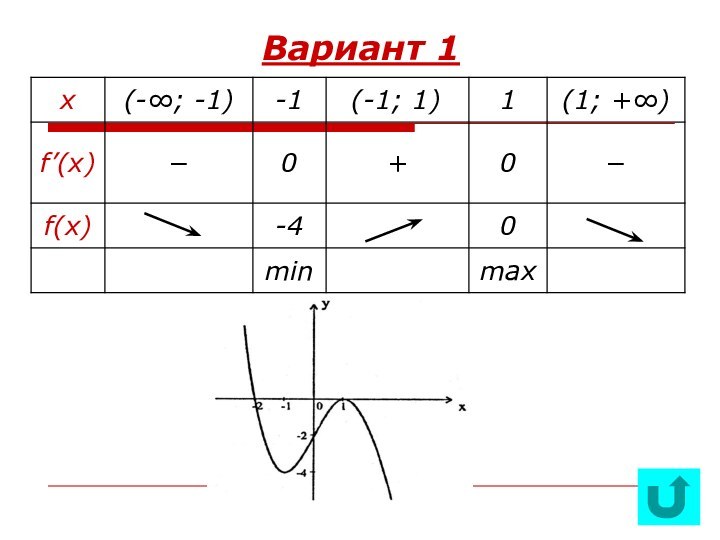
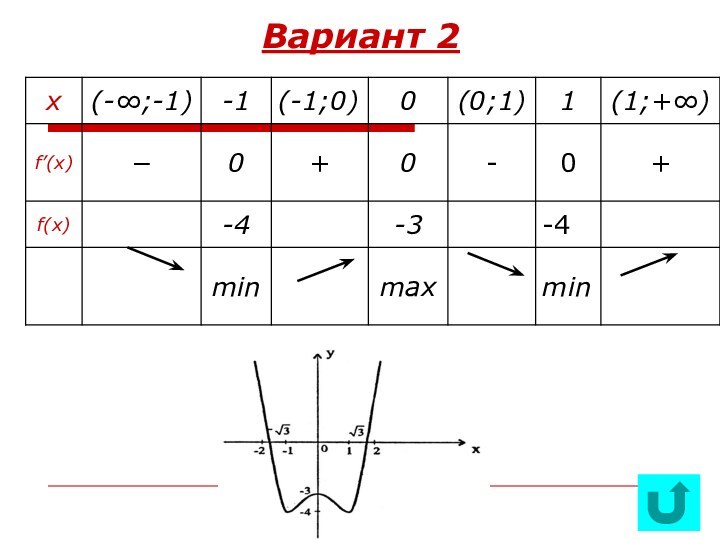
ПРИ ИССЛЕДОВАНИИФУНКЦИИ,ФОРМИРОВАНИЕ ПРИЕМОВ ОБОБЩЕНИЯ,
РАЗВИТИЕ ПРОСТРАНСТВЕННОГО МЫШЛЕНИЯ,
УМЕНИЕ ПРИМЕНЯТЬ
ЗНАНИЯ ПРИ ВЫПОЛНЕНИИ ПРАКТИЧЕСКОГО ЗАДАНИЯ.ВОСПИТАНИЕ ПОЛОЖИТЕЛЬНОГО ИНТЕРЕСА К ИЗУЧАЕМОМУ МАТЕРИАЛУ,
АКТИВИЗАЦИИ МЫСЛИТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ,
СОЗНАТЕЛЬНОЙ ДИСЦИПЛИНЫ, КУЛЬТУРЫ РЕЧИ.