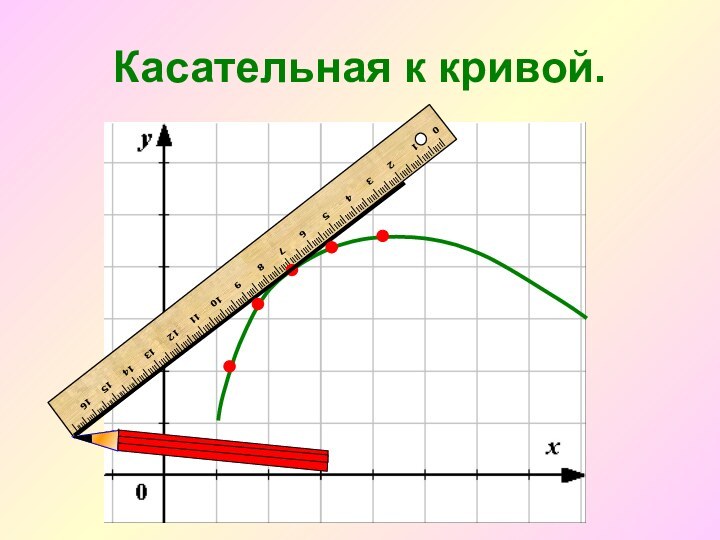
кривую линию, то эта продолженная таким образом сторона будет
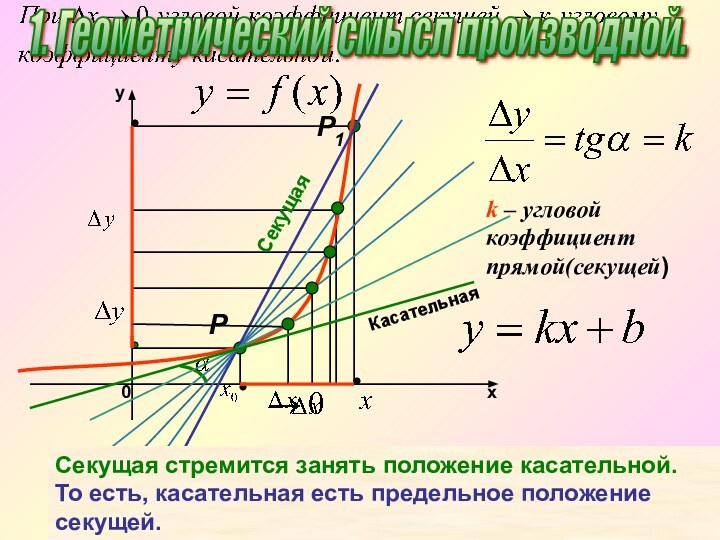
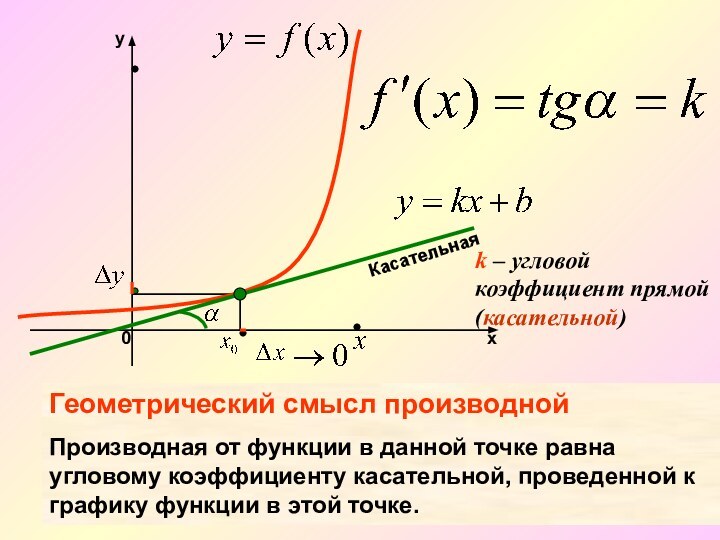
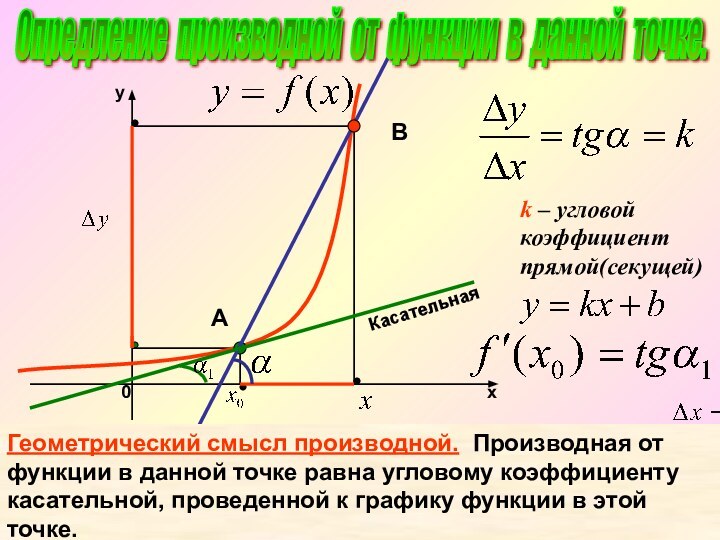
называться касательной к кривой.»1. Геометрический смысл производной.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






1. Геометрический смысл производной.
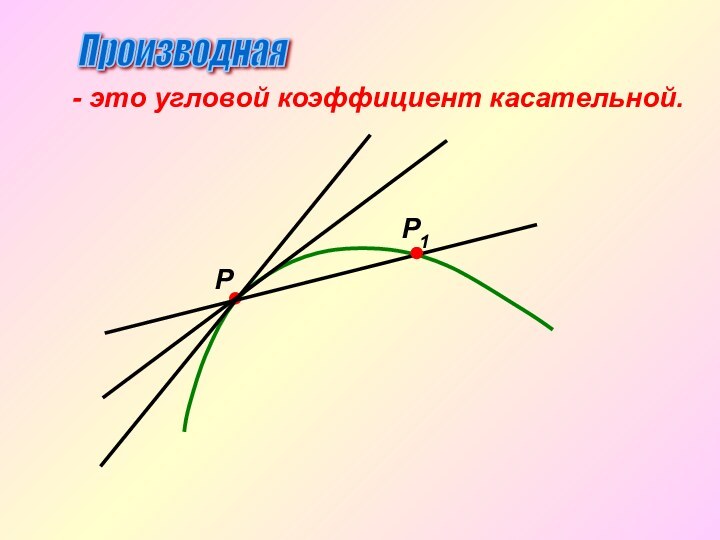
Секущая
1. Геометрический смысл производной.
Р
Р1
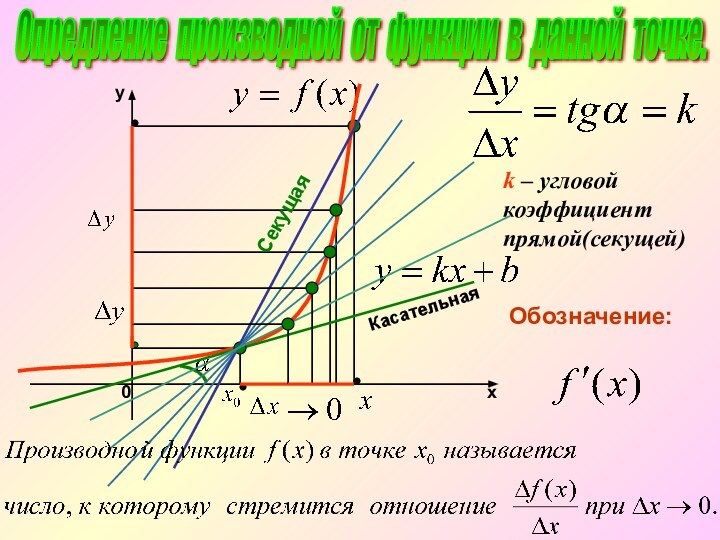
Опредление производной от функции в данной точке.
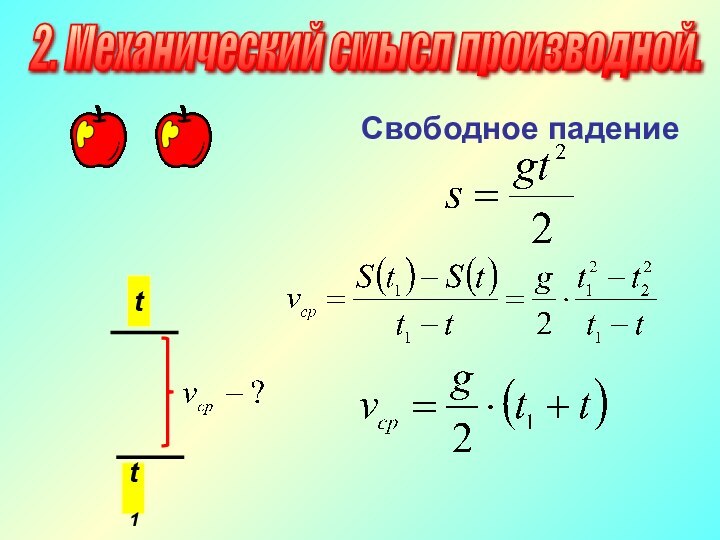
2. Механический смысл производной.
2. Механический смысл производной.
Производная
- это скорость