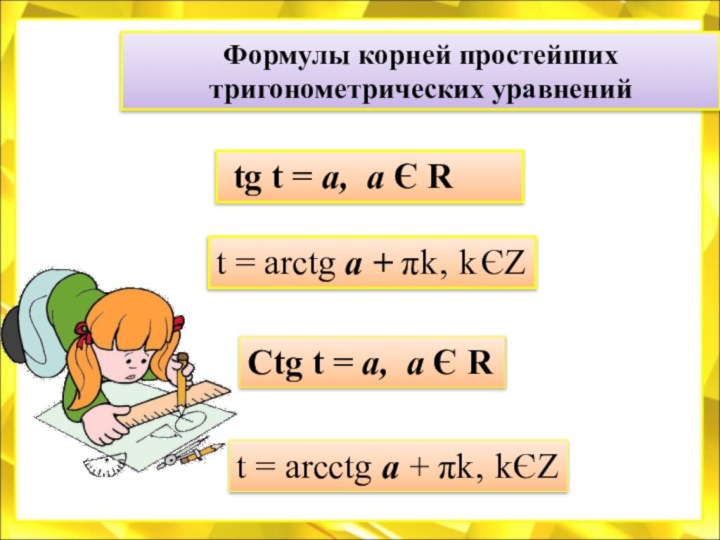
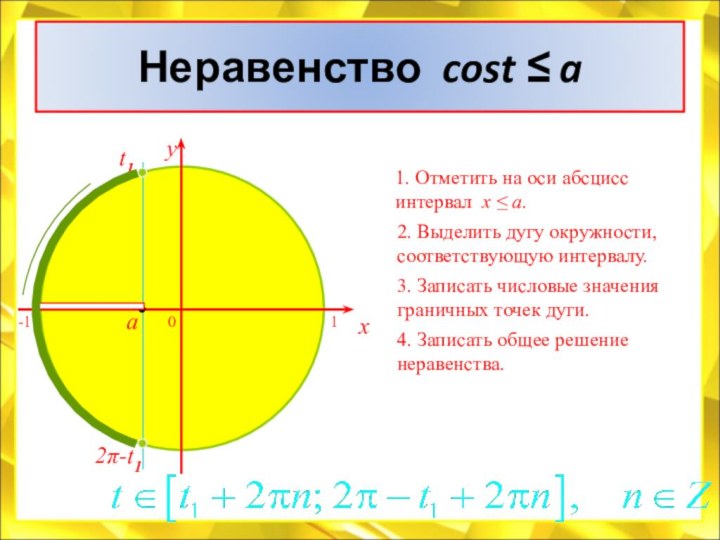
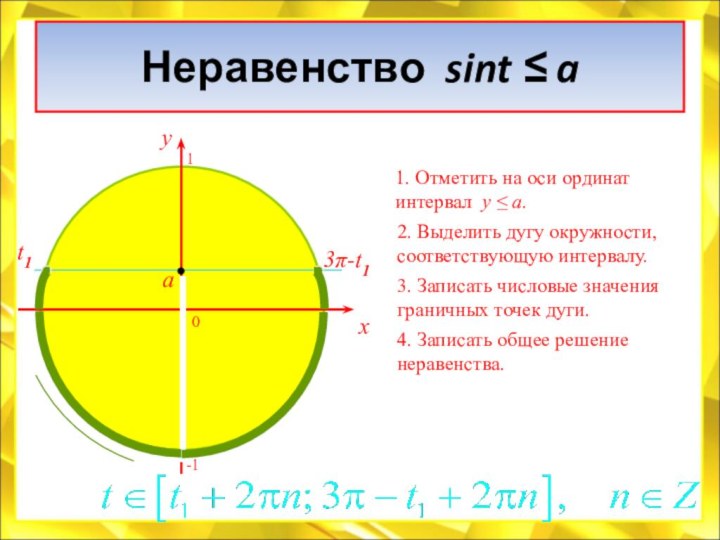
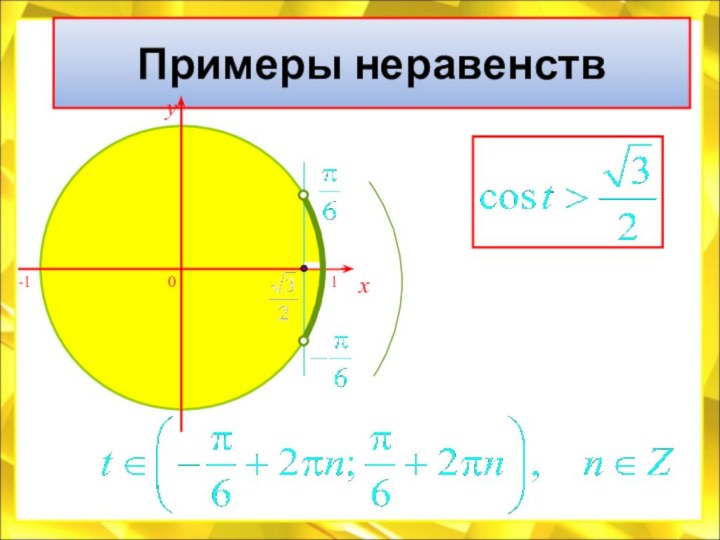
(измерять),
то есть измерение треугольников) — раздел математики,
в
котором изучаются тригонометрические функции и их приложения к геометрии. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (Bartholomäus Pitiscus, 1561—1613),
а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре.
Начало тригонометрии



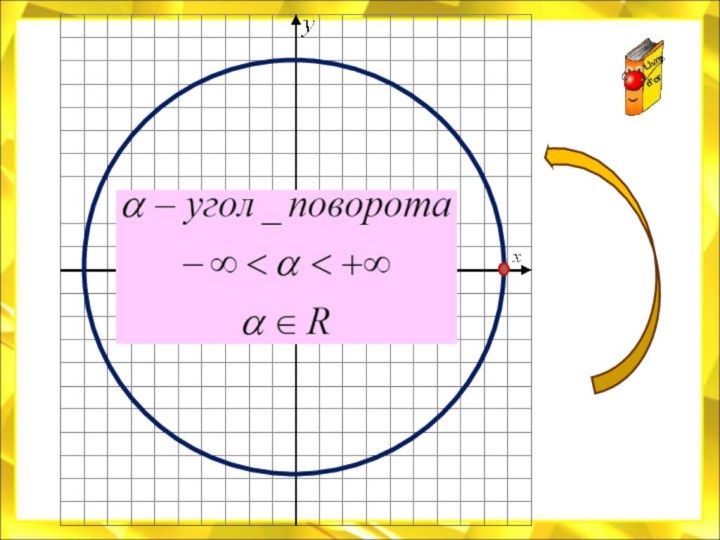
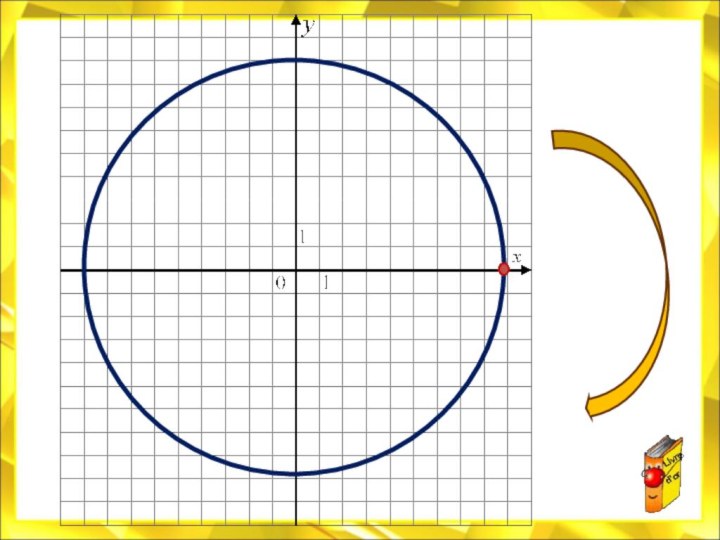

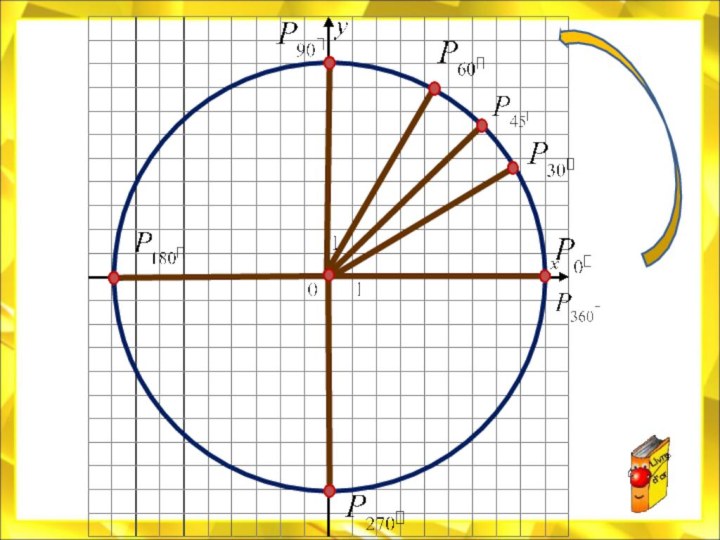
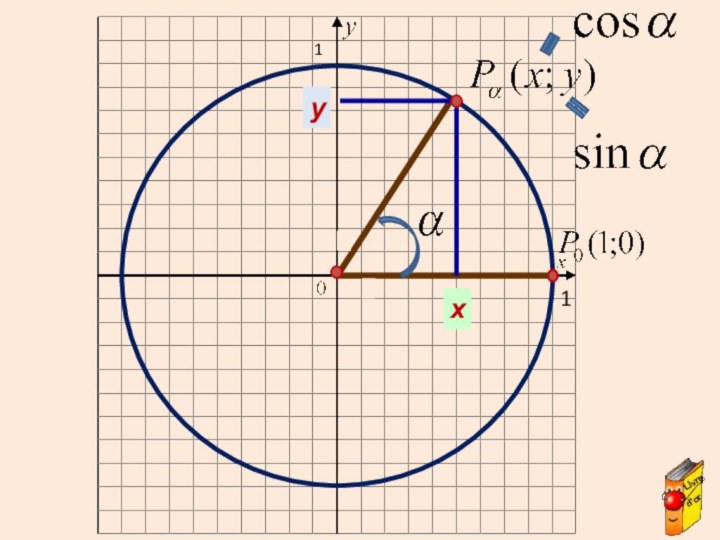











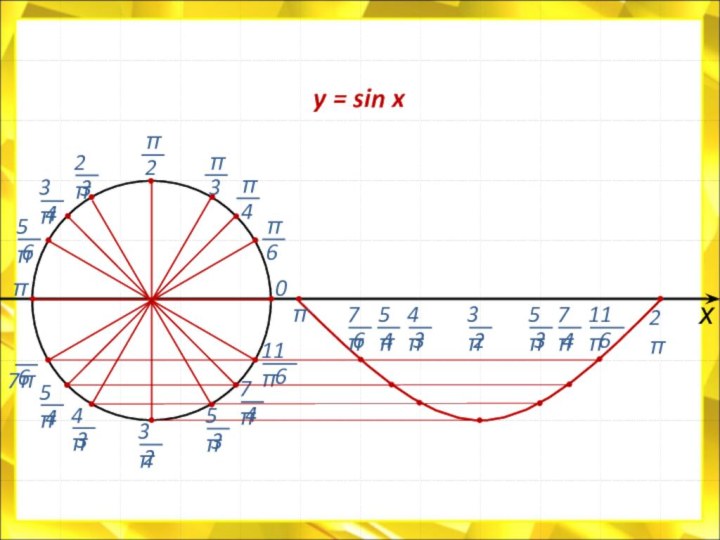
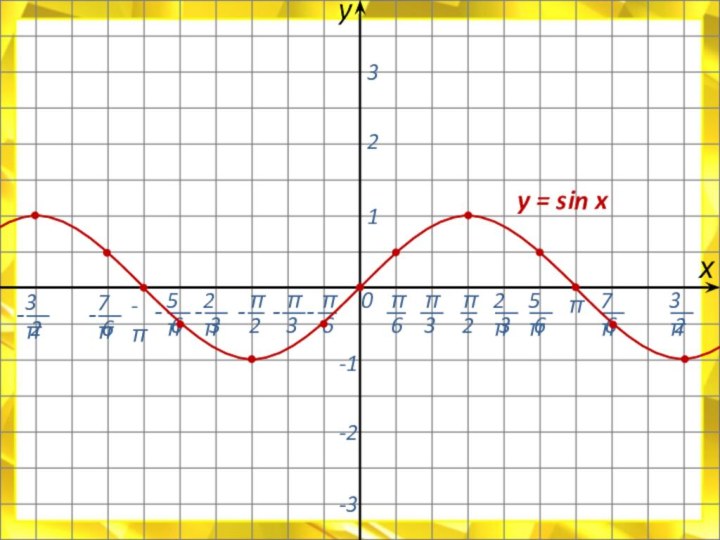
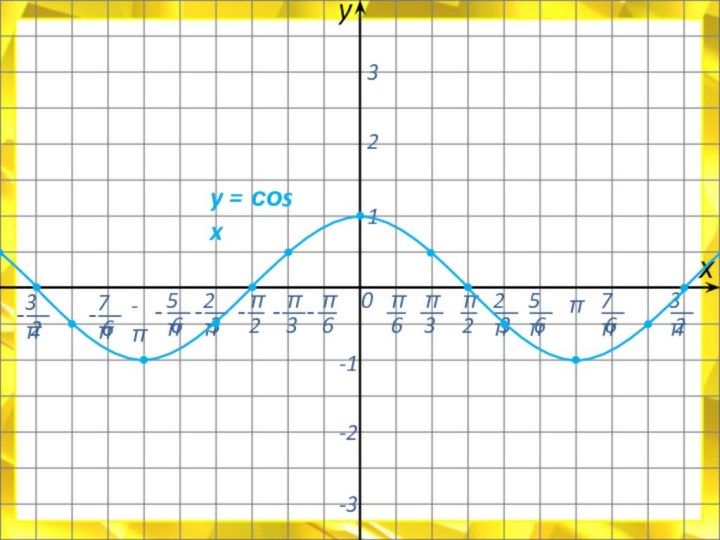
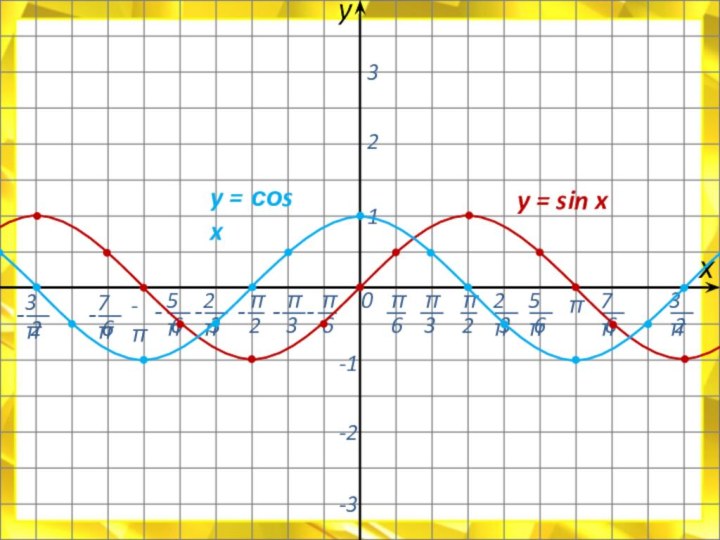
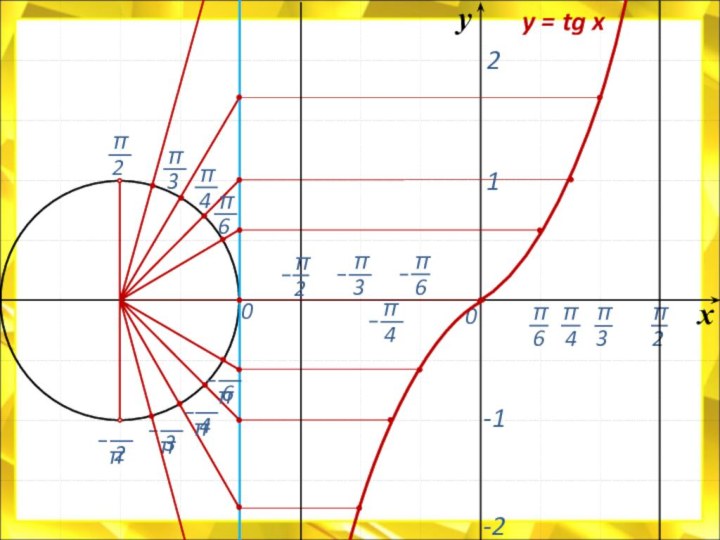
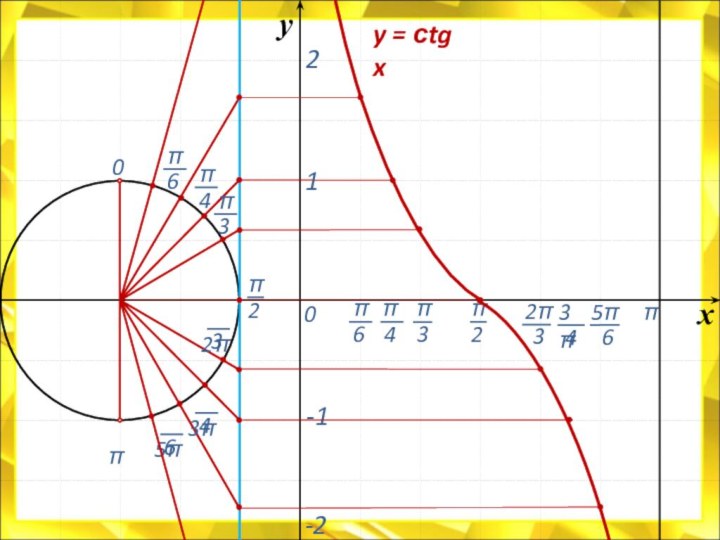
![Электронный учебник по тригонометрии Свойства функции:D(у) = R.E(у) = [- 1 ; 1]Функция периодическая; Т =](/img/tmb/7/614244/e70c52fdb4d40e8189e5d98362b2de91-720x.jpg)




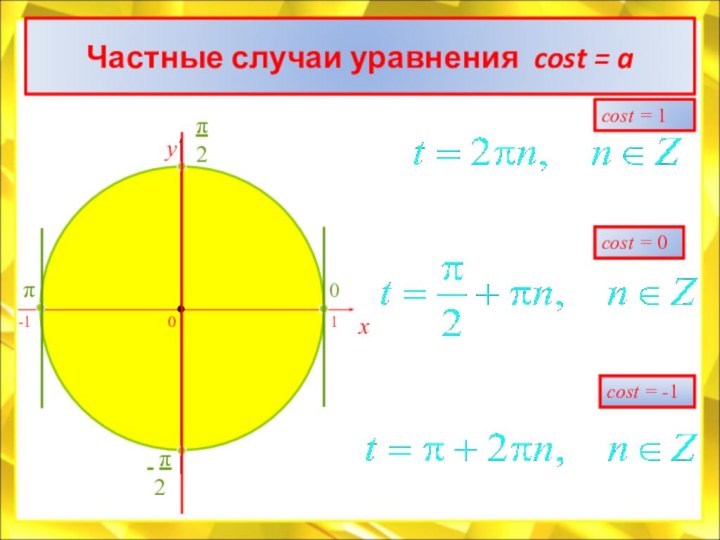


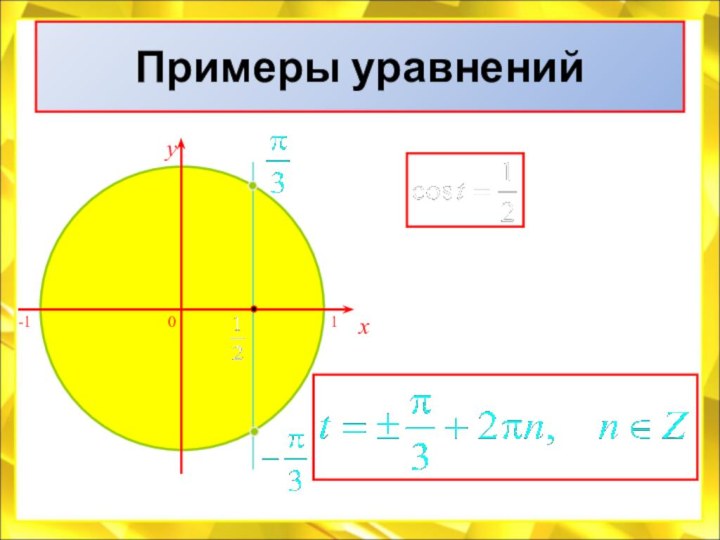
![Электронный учебник по тригонометрии Арккосинус0π1-1arccos(-а)Арккосинусом числа а называется такое число (угол) t из [0;π], чтоcos t](/img/tmb/7/614244/c6b27210ddc27cfd8b908f417f6d74a2-720x.jpg)