Презентация на тему Решение простейших тригонометрических уравнений

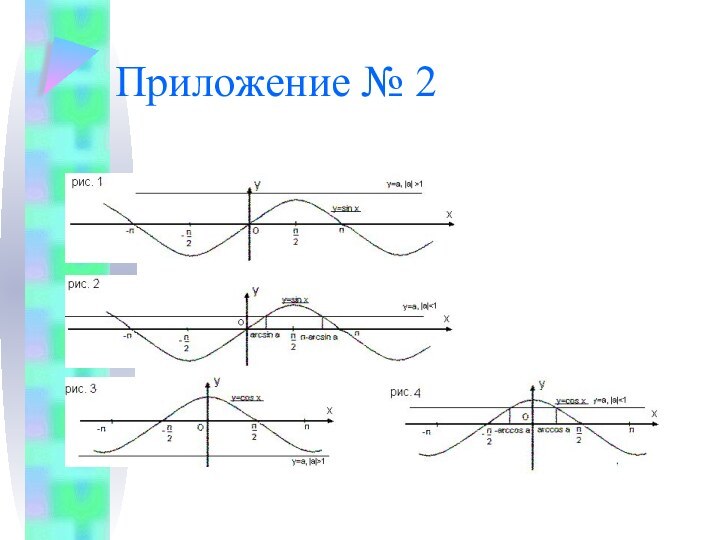
тригонометрических уравнений, сформировать у учащихся первичные умения и навыки

их решения;
Развивающие – развивать и совершенствовать у учащихся умение применять знания в изменённой ситуации; развивать логическое мышление, умение делать выводы и обобщения;
Воспитательные – воспитывать у учащихся аккуратность, культуру поведения, чувство ответственности.

к работе на уроке.
Взаимное приветствие; проверка подготовленности учащихся к

уроку (рабочее место, внешний вид); организация внимания.

Деятельность ученика

установить правильность и осознанность выполнения домашнего задания всеми учащимися.
1.

Проверка домашнего задания у доски.
а) Сравнить:
arc tg(- ½) и arccos√3/2
arc ctg (√3 и arc sin 1
б) Вычислить:
arc tg (-√3) + arc cos(- √3/2) + arc sin 1
arc sin (- 1) – 3/2arc cos ½ +
+ 3arc tg (- 1/√3)
в) расположить в порядке возрастания:
arc cos 0 , 4; arc cos (- 0,2); arc cos (- 0,8)

Деятельность ученика

Трое учащихся
решают данные
задания у интерактивной доски.

С классом проводится фронтальный опрос и устная работа
Вопросы:

а) Дать определение:
Arc sin α,
Arc cos α,
Arc tg α
Arc ctg α;
б) Имеют ли смысл выражения:
Arc sin 1/3
Arc cos 2/5
Arc tg 5
Arc ctg √3
Arc cos 1,8
Arc sin (- 1,5)

Деятельность ученика


Учащиеся отвечают на вопросы учителя, выполняют устные упражнения.

Найти значение выражений и мотивировать свой ответ:
arc sin 0
arc

cos ½
arc tg √3
arc ctg 1
г) Расположить в порядке возрастания:
arc sin ½; arc sin √3/2; arc sin √2/2;
arc cos 1; arc cos √2/2; arc cos √3/2.

Деятельность ученика
Учащиеся отвечают на вопросы учителя, выполняют устные упражнения.

Проверка работ, выполненных учащимися у доски.

4. Назовите несколько значений

угла поворота, при которых выполняются условия:
Sin α = ½;
Cos α = 1;
tg α = √3.

Деятельность ученика
Каждый учащийся, выполнявший работу, комментирует свой пример.
Предполагаемый вариант ответа:
α = arc sin ½ = π/6

Учитывая период функции синус α = arc sin ½ + 2π = 13π/6 и т.д.

познакомить учащихся с простейшими тригонометрическими уравнениями, вывести формулы и

отработать первичные навыки их решения.
Учитель диктует, а учащиеся записывают тему урока: «Решение простейших тригонометрических уравнений».
Открывается флиптчарт интерактивной доски, где записаны уравнения:
Sin t= a, cos t= a, tg t = a, ctg t = a

Деятельность ученика
Учащиеся привлекаются к определению координат точек пересечения графиков;
Делают выводы по ходу рассуждений вместе с учителем.

Полученные формулы записывают в тетрадь.

Даётся определение простейших тригонометрических уравнений.
2. Осуществляется решение уравнений: sin

t = 0, t = πn, nЄ Z;
Cos t = 0. t = π/2 + πn, nЄ Z;





Sin t = 0
Найдём на тригонометрической окружности точки с координатой 0.
Из А (1;0) в них можно попасть поворотом на угол πn,; т.е. t = πn, nЄ Z

Деятельность ученика

x

y

0

получают решения уравнения cos t = 0







t =

π/2 + πn, nЄ Z;

Деятельность ученика

y

x

0

уравнений
Sin t = 1, t = π/2 + 2πn,

nЄ Z;
Cos t = 1, t = 2πn, nЄ Z;
Sin t = -1, t = -π/2 + 2πn, nЄ Z;
Cos t = -1, t = π + 2πn, nЄ Z;
учащиеся по вариантам получают самостоятельно и осуществляют проверку через представленную учителем таблицу.
Получили формулы решения уравнений (Приложение №1)

Деятельность ученика

Выводятся формулы корней уравнений:
Sin t = a, cos t

= a, tg t = a.
а) Для вывода формулы корней уравнения sin t = a высвечивается флиптчарт с изображением в одной системе координат графиков функций y = sin x и y = a.
Если а > 1, (см. рис. 1, приложение № 2), то графики функций y = sin x и y = a не пересекаются, и уравнение sin t = a не имеет корней.
Если а < 1, (см. рис.2, приложение № 2), то на отрезке [-π/2; π/2] графики пересекаются в точке с абсциссой х = arc sin a, и , учитывая перид функции синус, получаем:
x= arc sin a + 2πn, nЄ Z; (1)

Деятельность ученика

отрезке [π/2; 3π/2] графики пересекаются в точке с абсциссой

x = π – arc sin a и, учитывая период, получаем:
x = π – arc sin a + 2πn, nЄ Z, (2)
Эти две формулы можно объединить одной:
t = (-1)n arc sin a + πn, nЄ Z, (3)
б) Аналогично выводятся формулы корней уравнений (см. приложение № 2, рис. 3, 4):
Cos t = a, t = +/- arc cos a+ 2πn,nЄ Z,
tg t = a , t = arc tg a + πn, nЄ Z.

Деятельность ученика

Для решения уравнений ctg t = a используется тождество

tg α * ctg α = 1,откуда tg α = 1/ctg α, и записывают уравнение в виде:
tg t = 1/a.
По окончании вывода формул высвечивается флиптчарт интерактивной доски с конспектом по теме урока (см. приложение № 3)

Деятельность ученика

уравнений
Ход урока, деятельность учителя
Задачи: первичное закрепление навыков решения тригонометрических

уравнений в ходе устной работы.
Устно решить уравнения:
Sin x = ½
Cos x = ½
Sin x = 3
Cos x = ¼
Cos x = - 2,4
tg x = 1
tg x = 1,7.
Решения высвечиваются на интерактивной доске по мере поступления ответов.

Деятельность ученика
Учащиеся, пользуясь полученными формулами, устно решают уравнения.

простейших тригонометрических уравнений.
Ход урока, деятельность учителя
Задачи: отрабатывать умения и

навыки решения уравнений.
У доски 4 учащихся по очереди решают по два уравнения:
а) 2sin x = 1, 2cos x = √3;
б) √2 cos x – 1 = 0, √3 tg x – 1 = 0;
в) sin 2x = √2 /2, cos x/3 = - ½;
г) tg x = 0,8, ctg x = 2,5

Деятельность ученика
Учащиеся работают вместе с отвечающими у доски или решают уравнения самостоятельно и сверяют решение с записями на доске.

навыков по теме в ходе самостоятельной работы.
Ход урока, деятельность

учителя
Задачи: проверить степень усвоения нового материала, выявить пробелы в знаниях учащихся.
Самостоятельная работа.
Решите уравнения:
1 вариант 2 вариант
Sin x = - √3/2 cos x = ½
Cos x = 1,1 sin x = √3
2sin x – 1 = 0 2cos x -√3 =0
tg 2x = 1 ctg 2x = 1

Деятельность ученика
Учащиеся выполняют самостоятельную работу,
по команде учителя обмениваются тетрадями и осуществляют взаимопроверку.
Верное решение показывается учителем на интерактивной доске.

домашнее задание, дать краткий инструктаж по его выполнению.

П.9, №

137 – 143 (г)

Деятельность ученика
Учащиеся записывают домашнее задание в тетради.