- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Решение квадратного неравенства с одной переменной(9 класс)
Содержание
- 2. Цели урока: образовательные: ввести понятие неравенства второй
- 4. Что называется квадратным трехчленом?Что надо сделать, чтобы
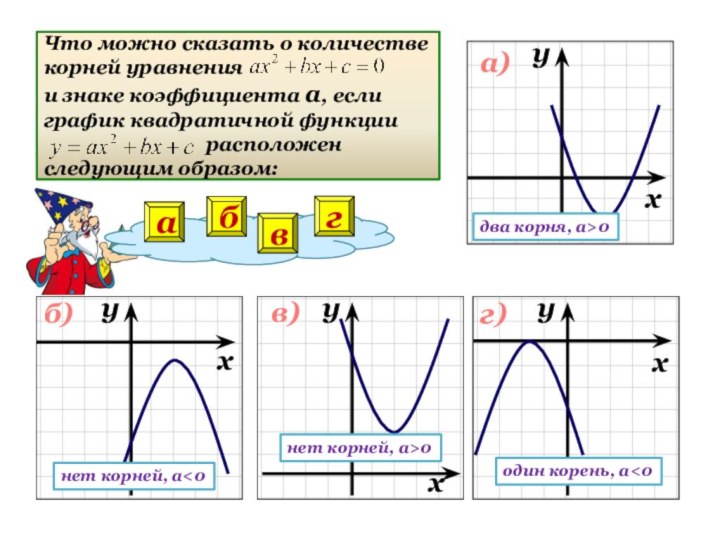
- 5. а)б)в)г)два корня, а>0бнет корней, а0вгодин корень, а
- 6. 00абв
- 7. Неравенства вида ах2 +
- 8. Алгоритм решения квадратного неравенства ax 2+ bx
- 9. Решить неравенство х² + 7 х −
- 10. ух0−32//////////3) Решение неравенствах² + х − 6
- 11. Решить неравенство − 2 х² + 5х
- 12. Решить неравенство 16 х² + 1 ≥
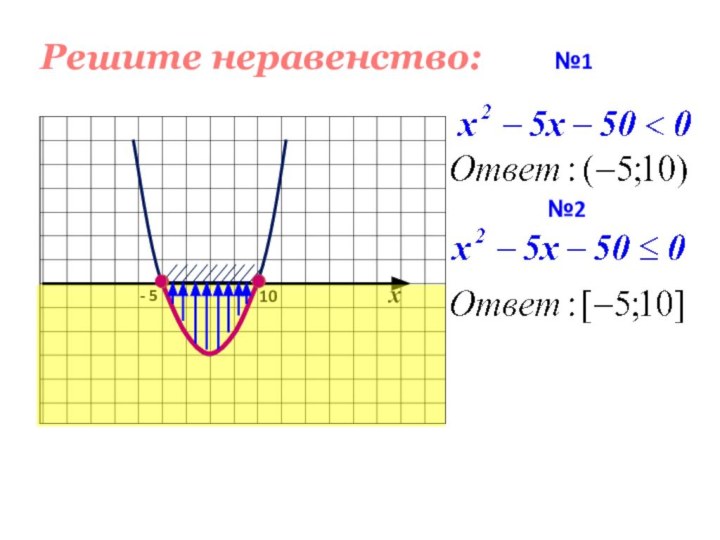
- 13. - 510№2Решите неравенство:№1
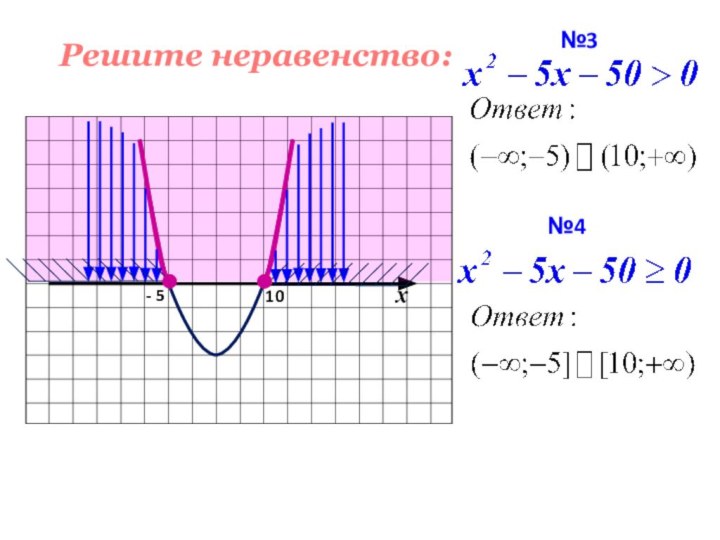
- 14. - 510№3№4Решите неравенство:
- 15. №5№6Решите неравенство:
- 16. -++Решите неравенство:26
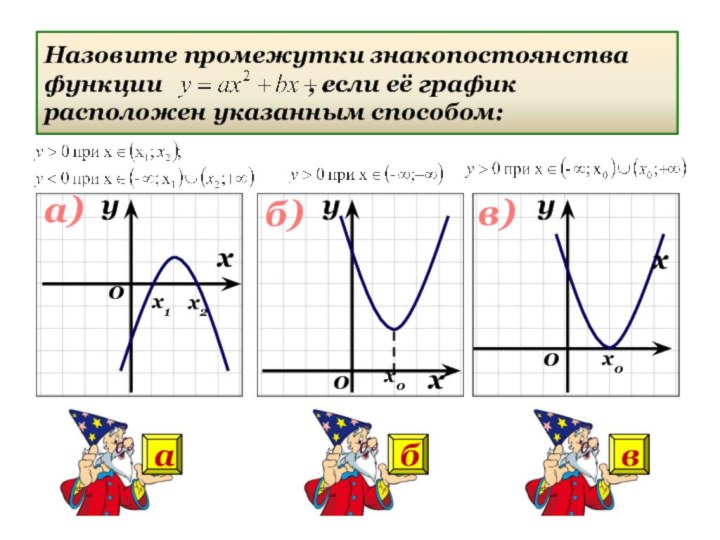
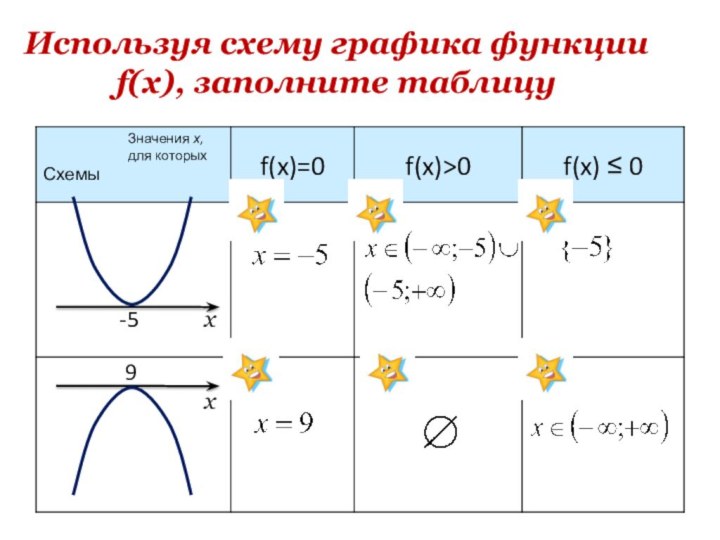
- 17. Используя схему графика функции f(x), заполните таблицу
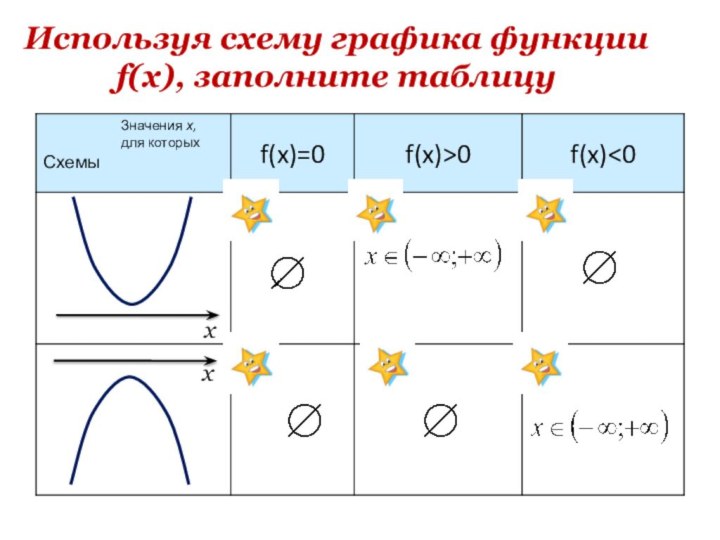
- 18. Используя схему графика функции f(x), заполните таблицу
- 19. Используя схему графика функции f(x), заполните таблицу
- 20. Блиц-опрос.Ученик решал квадратные неравенства и получилследующие ответы:а)
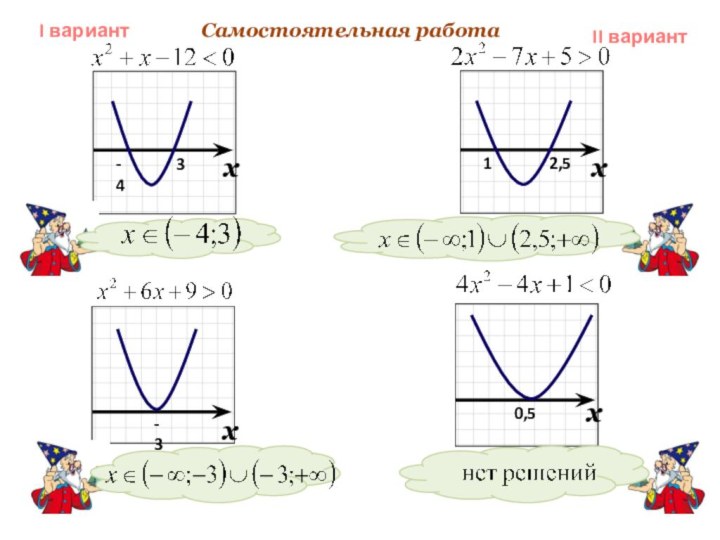
- 21. Самостоятельная работаI вариантII вариант
- 22. Скачать презентацию
- 23. Похожие презентации













Слайд 4
Что называется квадратным трехчленом?
Что надо сделать, чтобы найти
корни квадратного трехчлена?
Как называется функция вида у=ах2+bх+с?
Что является графиком
квадратичной функции?От чего зависит направление ветвей параболы?
Вопросы
Ответы
Слайд 7
Неравенства вида
ах2 + bх
+ c > 0, ах2 + bх + c
< 0,ах2 + bх + c 0, ах2+ bх + c 0,
где х – переменная, a, b, c - числа и а ≠ 0
называют неравенствами второй степени
с одной переменной или
квадратными неравенствами
Существует несколько способов решения
неравенств второй степени с одной переменной
Один из них - графический
Определение:
Слайд 9 Решить неравенство х² + 7 х − 8
≤ 0.
2) Ветви параболы у = х² +
7 х − 8 − направлены вверх,так как 1 > 0
у
х
0
−8
1
//////////////////////
●
●
3) Решение неравенства − все числа из промежутка [−8; 1]
Ответ: [−8; 1]
Решение. 1) Корни квадратного трёхчлена х² + 7 х − 8:
х² + 7 х − 8 = 0;
D = 49 + 32 = 81
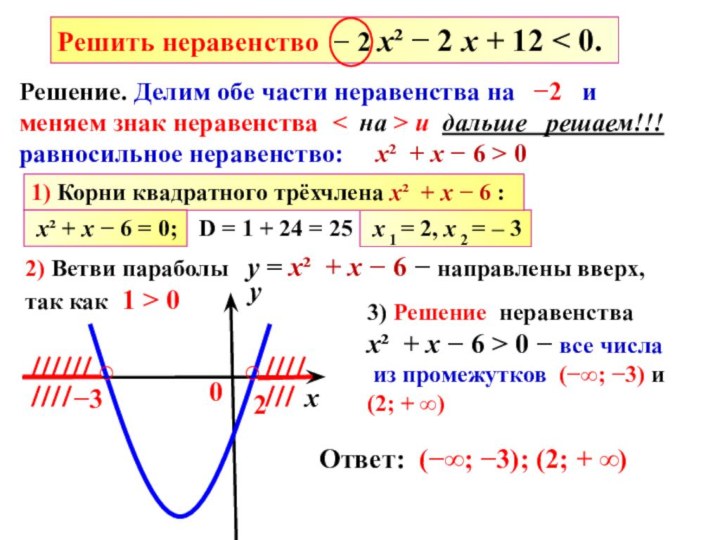
Слайд 10
у
х
0
−3
2
//////////
3) Решение неравенства
х² + х − 6 >
0 − все числа
из промежутков (−∞; −3) и
(2; + ∞)
Ответ: (−∞; −3); (2; + ∞)
Решить неравенство − 2 х² − 2 х + 12 < 0.
Решение. Делим обе части неравенства на −2 и
меняем знак неравенства < на > и дальше решаем!!!
равносильное неравенство: х² + х − 6 > 0
///////
○
○
D = 1 + 24 = 25
х 1 = 2, х 2 = – 3
2) Ветви параболы у = х² + х − 6 − направлены вверх,
так как 1 > 0
1) Корни квадратного трёхчлена х² + х − 6 :
х² + х − 6 = 0;
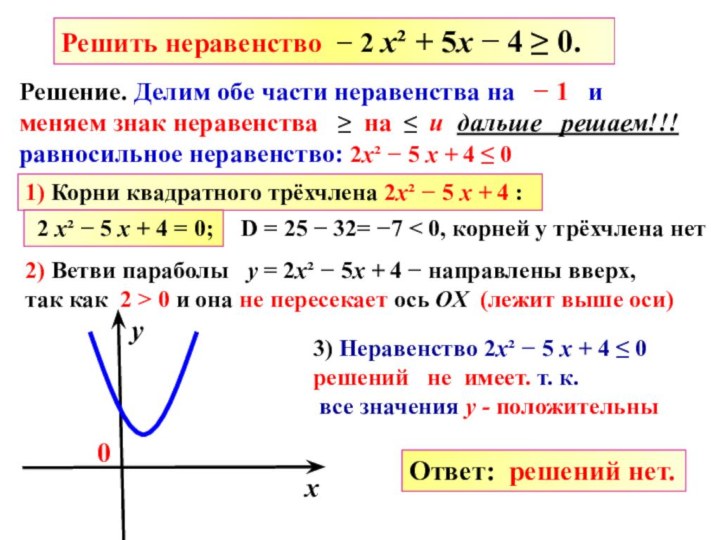
Слайд 11 Решить неравенство − 2 х² + 5х −
4 ≥ 0.
х
у
0
3) Неравенство 2х² − 5 х +
4 ≤ 0решений не имеет. т. к.
все значения у - положительны
Ответ: решений нет.
Решение. Делим обе части неравенства на − 1 и
меняем знак неравенства ≥ на ≤ и дальше решаем!!!
равносильное неравенство: 2х² − 5 х + 4 ≤ 0
1) Корни квадратного трёхчлена 2х² − 5 х + 4 :
2 х² − 5 х + 4 = 0;
D = 25 − 32= −7 < 0, корней у трёхчлена нет
2) Ветви параболы у = 2х² − 5х + 4 − направлены вверх,
так как 2 > 0 и она не пересекает ось ОХ (лежит выше оси)
Слайд 12 Решить неравенство 16 х² + 1 ≥ 8
х.
Решение. 1) Перепишем исходное неравенство в виде
16х²
− 8 х + 1 ≥ 0 или (4 х − 1)² ≥ 02) Очевидно, что решением неравенства (4 х − 1)² ≥ 0,
а значит, и исходного неравенства, являются
все действительные числа
Ответ: х − любое действительное число.
Слайд 20
Блиц-опрос.
Ученик решал квадратные неравенства и получил
следующие ответы:
а) х
< ± 2; б) −2 < х < 2;
в) х > ± 3; г) х > 3 и х < − 3.Как вы считаете, могли ли получиться такие ответы?
Если да, то придумайте неравенства, имеющие такие
решения;
если нет, объясните, почему вы так считаете.





























