Презентация на тему по математике на тему:Двугранный угол. Угол между плоскостями

угла.
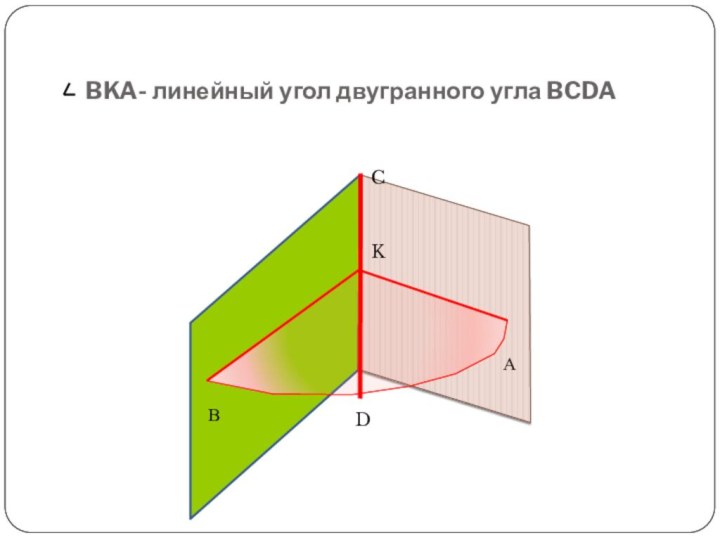
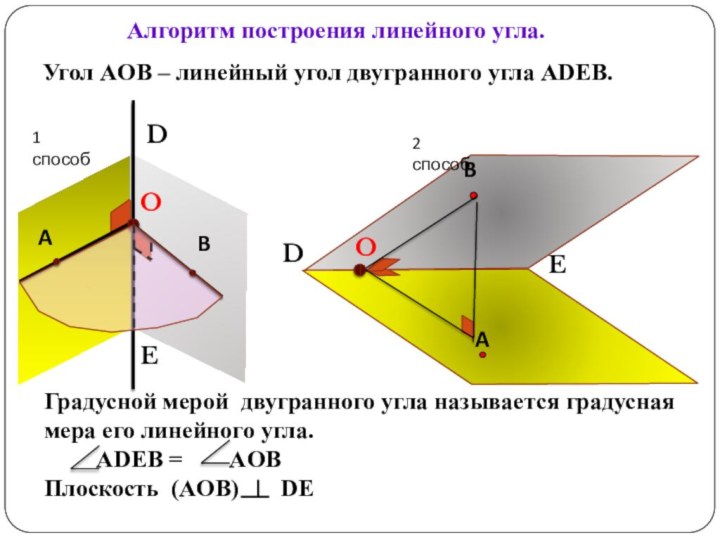
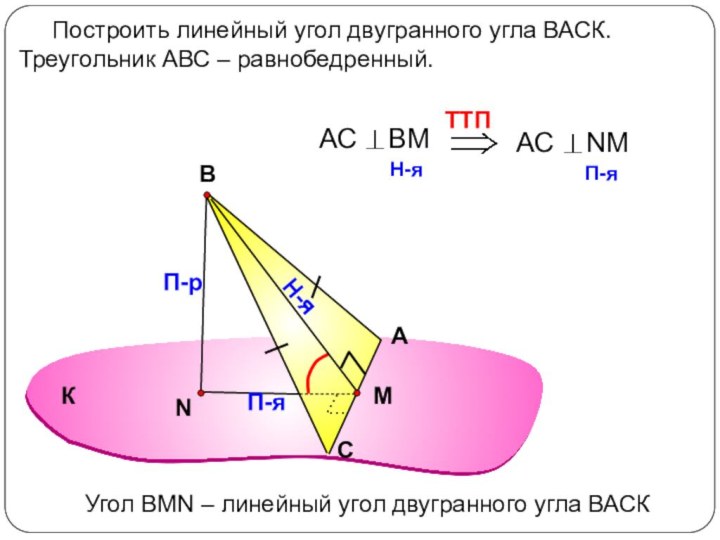
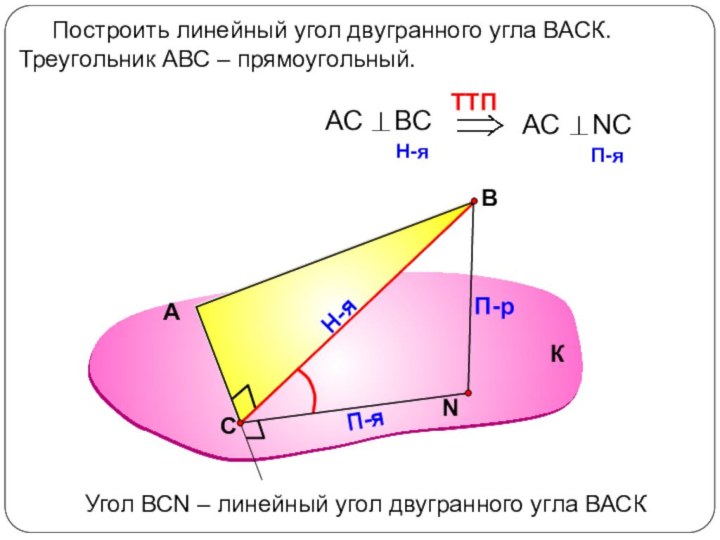
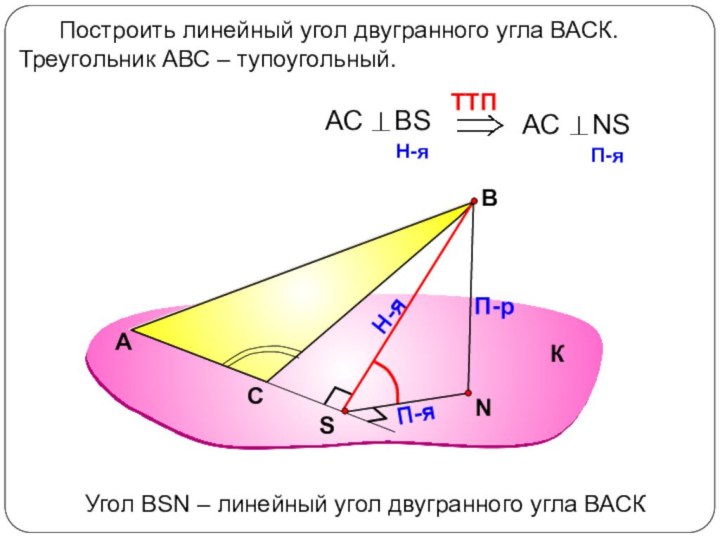
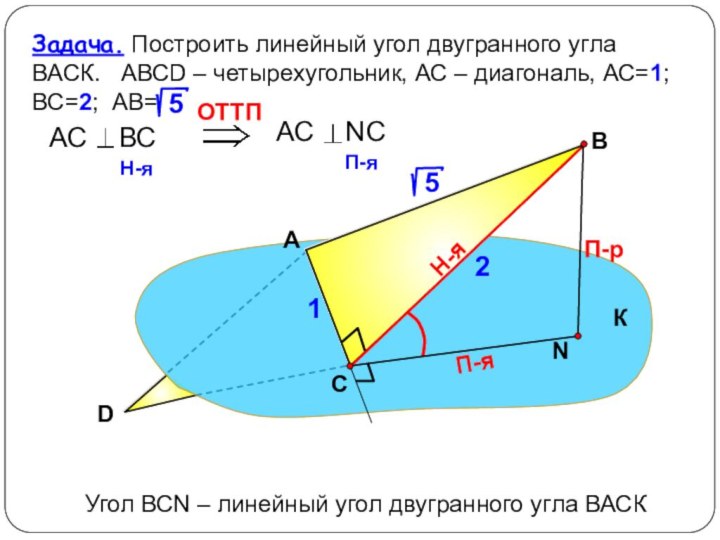
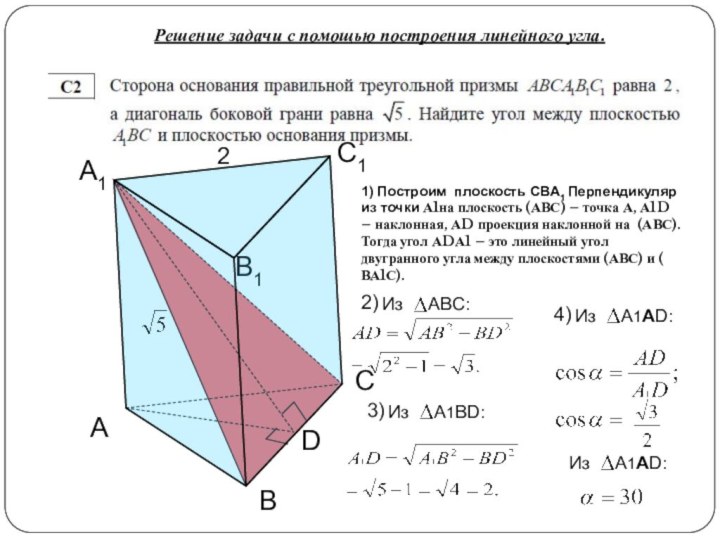
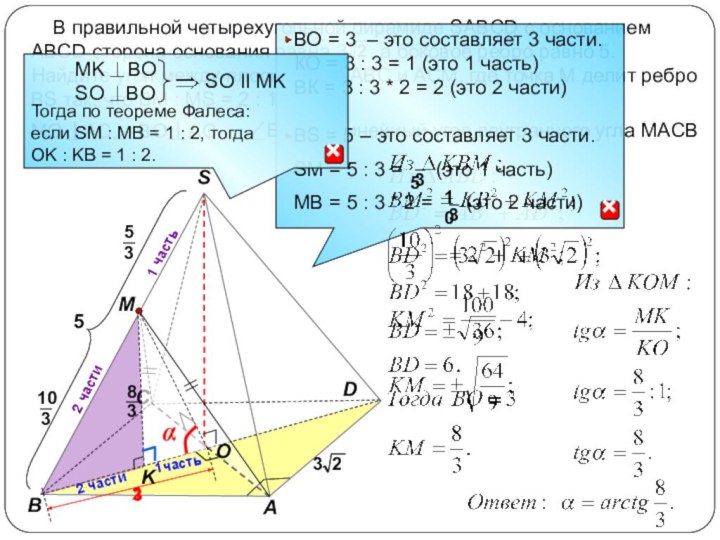
Сформулировать алгоритм построения линейного угла для данного двугранного.
Рассмотреть задачи

на построение линейного угла.
Повторить определение угла между прямой и плоскостью, признак перпендикулярности прямой и плоскости, теорему о трёх перпендикулярах ,
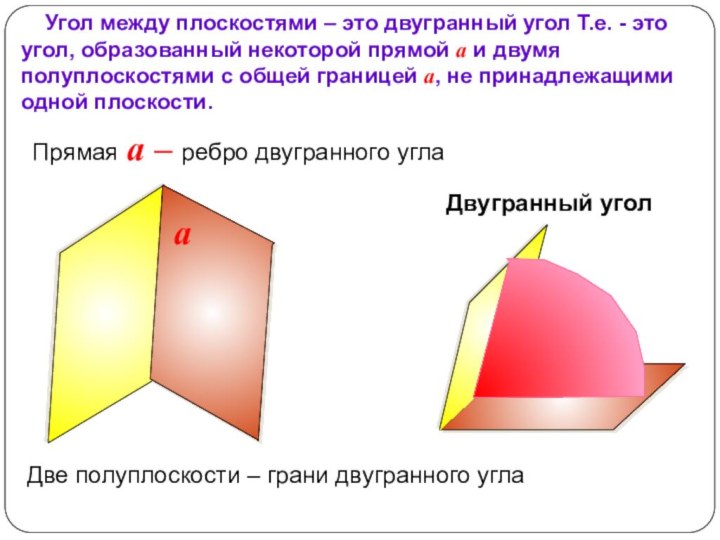
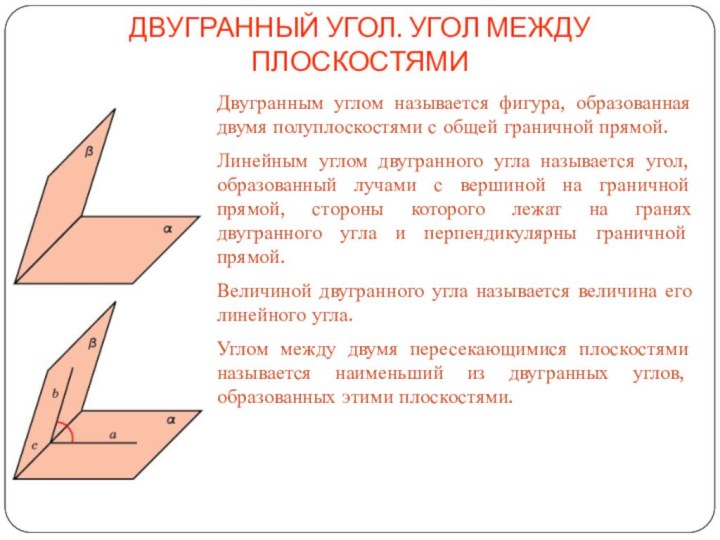
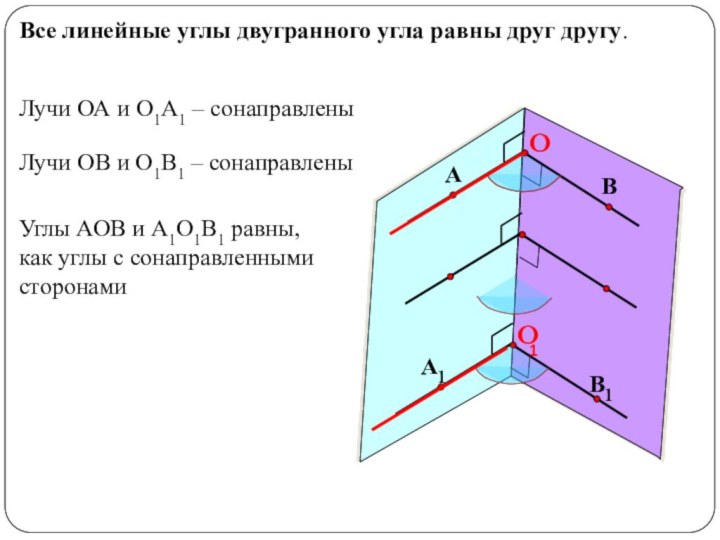
Ввести определение угла между плоскостями, доказать, что угол между плоскостями не зависит от выбора точки на прямой пересечения плоскостей.

a

α

а- общая граница полуплоскостей называется ребром двугранного угла.
Полуплоскости,

образующие двугранный угол, называются его гранями
Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не прилежащими одной плоскости

а

угол Т.е. - это угол, образованный некоторой прямой a

и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости.

Прямая a – ребро двугранного угла

a

Две полуплоскости – грани двугранного угла

Двугранный угол

собой двугранных углов.
Величиной угла между плоскостями называется величина

меньшего двугранного угла.

Величиной угла между плоскостями называется

величина меньшего двугранного угла.

Величина двугранного угла
измеряется величиной соответствующего линейного угла.

образованная двумя полуплоскостями с общей граничной прямой.
Линейным углом

двугранного угла называется угол, образованный лучами с вершиной на граничной прямой, стороны которого лежат на гранях двугранного угла и перпендикулярны граничной прямой.
Величиной двугранного угла называется величина его линейного угла.
Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных этими плоскостями.

мерой двугранного угла называется градусная мера его линейного угла.

ADEB = AOB
Плоскость (AOB) DE

Алгоритм построения линейного угла.

D

E

O

1 способ

2 способ

ОА и О1А1 – сонаправлены
Лучи ОВ и О1В1

– сонаправлены

Углы АОВ и А1О1В1 равны,
как углы с сонаправленными сторонами

ВАСК.
Треугольник АВС – равнобедренный.
А
С
В
П-р
Н-я
П-я
Угол ВMN – линейный угол двугранного

угла ВАСК

К

ВАСК.
Треугольник АВС – прямоугольный.
А
В
П-р
Н-я
П-я
Угол ВСN – линейный угол двугранного

угла ВАСК

К

С

ВАСК.
Треугольник АВС – тупоугольный.
А
В
П-р
Н-я
П-я
Угол ВSN – линейный угол двугранного

угла ВАСК

К

С

АВСD – четырехугольник, АС – диагональ, АС=1; ВС=2; АВ=
А
В
П-р
Н-я
П-я
Угол

ВСN – линейный угол двугранного угла ВАСК

К

С

D

2

1

Построить линейный угол двугранного угла ВАСК.

АВСD – четырехугольник, АС – диагональ; АС=5, ВС= 6, АВ= 9.

А

В

П-р

Н-я

П-я

Угол ВSN – линейный угол двугранного угла ВАСК

К

С

D

9

6

5

тупой

Задача.

Дан куб. Найдите следующие

двугранные углы:
a) АВВ1С; б) АDD1B; в) А1ВВ1К, где K – середина
ребра А1D1.

А

В

D1

С

А1

D

С1

Угол АВС – линейный угол двугранного угла АВВ1С. Прямой, т.к. АВСД – квадрат.

В1

Угол АDВ – линейный угол двугранного угла АDD1B. Равен 450 , т.к. D1B –диагональ квадрата.

Угол А1В1К– линейный угол двугранного угла А1ВВ1К

В треугольнике А1КВ1 угол А1 –прямой, катеты равны 1 и 0,5.

плоскость СBА1 Перпендикуляр из точки А1на плоскость (АВС) –

точка А, А1D – наклонная, АD проекция наклонной на (АВС). Тогда угол АDА1 – это линейный угол двугранного угла между плоскостями (АВС) и ( ВА1С).

ребер соответственно
A1B1 и A1D1. Найдите тангенс

угла между плоскостями AEF и BDD1.

B

A

D

C

C1

A1

B1

D1

1) Заменим плоскость DBB1 на параллельную плоскостьFEKL. Угол между плоскостями AEF и BDD1 равен углу между плоскостями AEF и FEK.

2) Ребро двугранного угла – FE.

3) Строим линейный угол двугранного угла AFEK.

a

a

Решение задачи построением параллельной плоскости.

ребра CD , AB = 3 , BC =

2 , BB1 = 2. Найдите угол между плоскостями AB1N и ABC .


В правильной четырехугольной пирамиде SABCD с основанием ABCD сторона основания равна 3, а боковое ребро равно 5. Найдите угол между плоскостями ABC и ACM, где точка M делит ребро BS так, что BM : MS = 2 : 1.

Домашнее задание