случаям, из которых m случаев благоприятны событию А, а
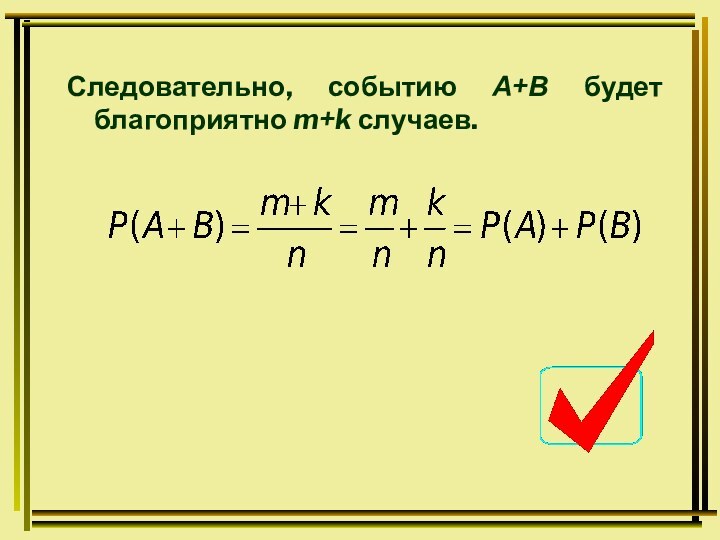
k - случаев благоприятны событию В.Тогда вероятности событий А и В будут равны соответственно:
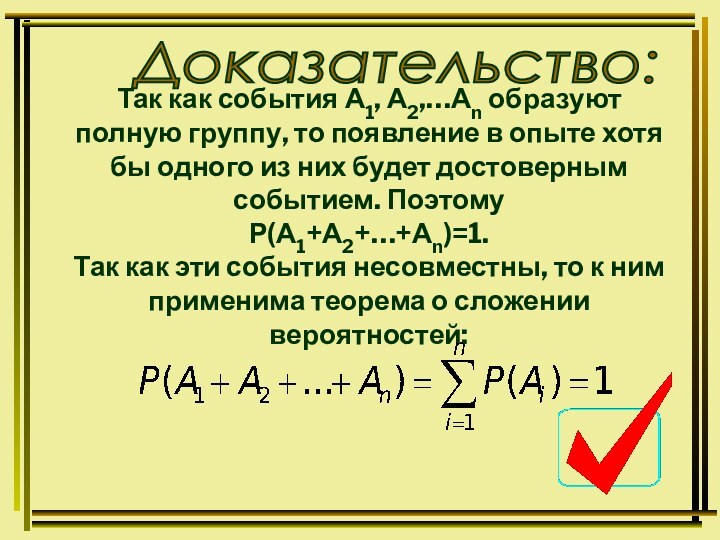
Доказательство:
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


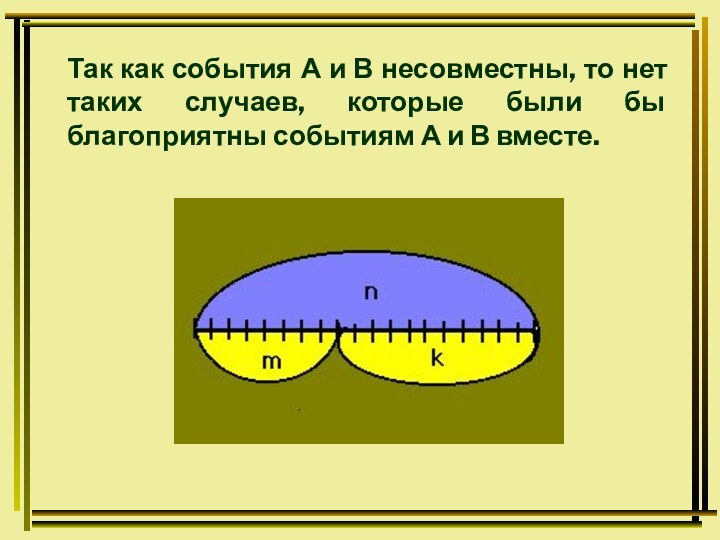








Доказательство:
Доказательство:
Пусть событие А заключается в том, что случайно выбранный сотрудник принадлежит к партии любителей пива, а событие В - что сотрудник принадлежит к партии зеленых.
Решение.
Т.к. эти события несовместны, то применяем теорему о сложении вероятностей в виде:
Р(А+В+С)=Р(А)+Р(В)+Р(С)