Слайд 2
План лекции:
Предмет и задачи биологической статистики.
Данные:
а) Виды данных
б) Шкалы измерения данных
в) Графическое представление данных
3. Выборочный метод.
Слайд 3
XXI век – век доказательной медицины.
Большую роль в
медицине играют методы точных наук, в первую очередь статистики.
Слайд 4
В чем суть доказательной медицины?
Д. м. требует, чтобы
при решении задач медицинской практики использовались результаты лучших клинических
испытаний, в надежности и доброкачественности которых нет никаких сомнений.
Д.м. значительно сокращает и облегчает перенос научных достижений в медицинскую практику.
Слайд 5
Практикующий врач должен понимать современный статистический язык
и знать методологию современной медицины. В ином случае врач
не сможет эффективно пополнять свои знания при чтении современных медицинских публикаций.
Внедрение в практику принципов д.м. диктует современному выпускнику мед. вузов необходимость понимания биостатистики.
Слайд 6
Статистика
- Это наука, позволяющая увидеть закономерности в хаосе
случайных данных, выделить устойчивые связи в них, определить действия
с тем, чтобы увеличить долю правильно принятых решений среди всех принимаемых.
Слайд 7
Статистика
Это сбор, группировка, систематизация,
представление, анализ и интерпретация
данных (результатов наблюдений).
Это изучение генеральных совокупностей и их
изменчивости.
Слайд 8
Статистика
промышленная,
сельскохозяйственная,
коммунальная,
судебная,
и другие,
биологическая
– изучающая вопросы
связанные с медициной и биологией.
Слайд 9
Биологическая статистика
- система знаний о правилах планирования и
анализа результатов натурных и экспериментальных исследований биологических объектов.
Слайд 10
Биостатистика-как дисциплина
Предмет – основные положения и методы биологической
статистики.
Цель дисциплины – научить правильно количественно оценивать процессы, происходящие
в живой природе.
Задачи дисциплины – познакомить и научить пользоваться основными статистическими критериями для оценки биологических совокупностей.
Слайд 11
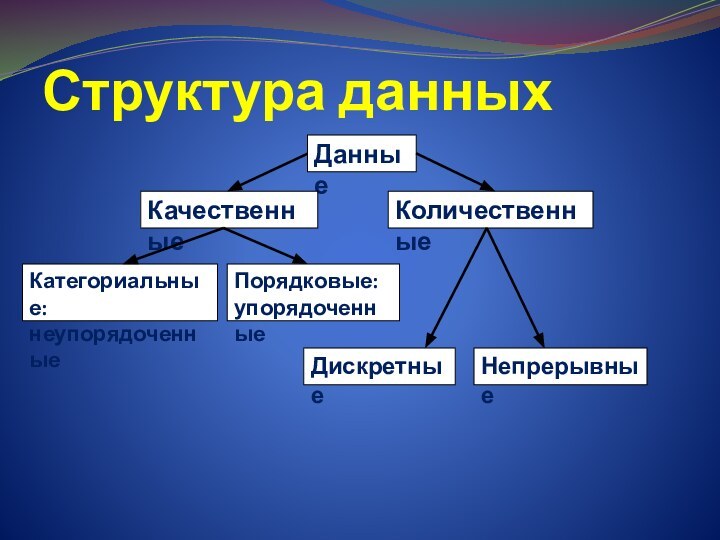
Структура данных
Данные
Качественные
Количественные
Категориальные:
неупорядоченные
Порядковые:
упорядоченные
Дискретные
Непрерывные
Слайд 12
Качественные данные
Номинальные или категориальные (классификационные):
Данные разбиты на категории,
названия которых отражают значения признака или классификационный номер.
Данные этого
типа нельзя измерять или упорядочивать по значению, над ними нельзя выполнять арифметические операции.
Примеры: пол, семейное положение, этническая группа, статус занятости, группа крови.
Слайд 13
Качественные данные
Порядковые (ранговые):
Данные относятся к непересекающимся категориям, в
зависимости от степени проявления у них анализируемого признака. Категории
(градации, уровни) логически упорядочены в соответствии со шкалой относительной значимости значений.
Над данными нельзя выполнять арифметические операции.
Примеры: стадии заболевания, выраженность боли (шкала оценки боли), классы общества.
Слайд 14
Качественные данные
Бинарные или дихотомические:
Номинальные или категориальные данные, которые
распределяются по двум непересекающимся категориям.
Примеры: мертвый / живой, излеченный
/ не излеченный.
Слайд 15
Количественные (числовые) данные
Дискретные числовые :
Данные могут иметь только
строго фиксированные числовые значения, обычно целые. Значения данных изменяются
скачкообразно, и никаких промежуточных значений не существует.
Для этих данных важны и величина, и порядок.
Примеры: количество дней, число пациентов.
Слайд 16
Количественные (числовые) данные
Непрерывные числовые :
Данные могут принимать любое
числовое значение из заданного диапазона (отрезка). Количество значений бесконечно,
значения могут содержать дробную составляющую, зависящую от точности измерений.
Примеры: температура, вес, рост, давление.
Слайд 17
Графическое представление данных
Применяется для:
Распознавания структуры и характерных особенностей
данных;
Обнаружения ошибок в данных;
Исследования взаимосвязи между случайными
величинами;
Оценки соответствия данных выбранным моделям;
Обнаружения новых явлений;
Выявления необходимости в корректировке данных, а
также определения способа ее осуществления
(преобразование данных, сбор дополнительных данных
или изменение условий эксперимента).
Слайд 18
Графическое представление дискретных данных
Таблица
Столбиковая диаграмма
Круговая диаграмма
Точечный график
и
т.д.
Слайд 19
Графическое представление непрерывных данных
Группированная выборка
Гистограмма
Диаграмма «Стебель с листьями»
и
т.д.
Слайд 20
Множество объектов, характеризуемых некоторым качественным или количественным
признаком, называется статистической совокупностью.
Статистическая совокупность, состоящая из всех объектов,
которые ( по крайней мере, теоретически) подлежат обследованию, называется генеральной статистической совокупностью.
Статистическая совокупность, состоящая из некоторого количества объектов, случайным образом отобранных из соответствующей генеральной совокупности, называется выборочной совокупностью или просто выборкой.
Слайд 21
Метод статистического исследования, состоящий в том, что
на основе изучения выборочной совокупности делается заключение о всей
генеральной совокупности, называется выборочным методом.
Основные требования к выборке – хорошо представлять генеральную совокупность, то есть быть представительной (репрезентативной).
Слайд 22
Репрезентативность:
случайностью выбора объектов из генеральной совокупности, когда
каждому из них обеспечивается одинаковая возможность быть отобранным;
независимостью
результатов наблюдений в выборе;
правильным определением объема выборки с учетом всех конкретных условий.
Слайд 23
Числовые характеристики выборки:
выборочная средняя:
выборочная дисперсия:
выборочное
среднеквадратичное отклонение:
Слайд 24
Точечные и интервальные оценки параметров совокупности.
Точечной называют оценку,
которая определяется одним числом.
Интервальная - двумя числами.
Слайд 25
доверительная вероятность:
Р=0,95 (95%),
уровень значимости:
α
=1-0,95=0,05 (5%)
Слайд 26
Точечные оценки параметров ген. совокупности:
генеральная средняя:
Слайд 27
Интервальные оценки параметров совокупности.
Интервал, который с заданной вероятностью
(надежностью) покрывает неизвестный параметр, называется доверительным интервалом.
Вероятности, признанные достаточными
для уверенного суждения о генеральных параметрах на основании известных выборочных показателей, называются доверительными вероятностями.
Слайд 28
Доверительный интервал для выборочного среднего значения:
где
tα- коэффициент Стьюдента
стандартная ошибка среднего:
Слайд 29
Литература:
Лукьянова Е.А. Медицинская статистика. – М: Изд. РУДН,
2002.
Медик В.А., Токмачев М.С., Фишман Б.Б. Теоретическая статистика//Статистика в
медицине и биологии. В 2-х томах / Под. ред. проф. Ю.М Комарова. Т.1. – М.: Медицина, 2000.
Гланц С. Медико-биологическая статистика. – М.: Практика, 1999.
Рокицкий П.Ф. Биологическая статистика. – Высшая школа, 1973.