Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Метод проецирования. Ортогональный чертеж точки и прямой линии

Содержание

Тема 2. Метод проецирования. Ортогональный чертеж точки и прямой линии
Уральский федеральный университет имени первого Президента России Б.Н. Ельцина Кафедра “Инженерная Тема 2. Метод проецирования. Ортогональный чертеж точки и прямой линии Цель и задачи лекцииОпределить основы построения ортогонального чертежаДать понятия октантов пространстваРаскрыть сущность В результате изучения темы Вы будете знатьВиды проецирования в начертательной геометрииОртогональную систему - НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ -занимается построением изображений и изучением пространственных объектов по Основные задачи начертательной геометрииСоздание – чертежа или эпюра Решение задач на плоскости3. Проецирование – процесс получения на чертеже достоверного изображения, по которому можно Виды проецированияЦентральноеПараллельноеОртогональноелучи плоскостипроекций АксонометрическоеПерспективаЛекция 2. Метод проецирования. Проекция – изображение, полученное проецированием объекта на плоскость или какую-либо другую поверхностьЛекция S – центр проецирования;П – плоскость проекций;А, В, С – точки Параллельное проецированиеs – направление проецирования;П – плоскость проекций;А, В, С – точки Ортогональное проецированиеВпСпСВАПsАп1.Направление проецирования - s;2. Плоскость проекций - П ; АпВпСпСВАПSАПВССпАпВпЛекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линииПараллельное и центральное проецирование Формирование ортогональной системы плоскостей и осей координатП1Горизонтальная плоскость проекций - П1Лекция 2. П2П1Горизонтальная плоскость проекцийФронтальная плоскость проекций – П2 Горизонтальная плоскость проекций - П1 Фронтальная плоскость проекций - П2 Ортогональные проекции точки А1 - горизонтальная проекция точки А; А2 - фронтальная ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ - ЭПЮРОртогональный чертеж или эпюр - изображение полученное путем параллельного Задание точки на эпюреТочку можно задать ее координатами, например:А(50; 20: 45)В(20; 40; Задание точки на эпюреТочку можно задать ее изображением и измерить ее координаты, Задание точки на эпюреТочку можно задать ее положением относительно плоскостей проекций, например:D Задание точки на эпюреТочку можно задать ее положением относительно другой точки, например:В(20; По двум проекциям точки всегда можно построить третью проекцию точкиXZY0B2B1П1П2С2С1С3П3Лекция 2. Метод Конкурирующие точкиТочки, лежащие на одной линии связи, называются конкурирующимиА2А1≡В1В2С2 ≡С1D1D2Лекция 2. Метод Эпюры могут бытьС осями координатБезосными B2B1П1П2С2С1С3П3С2С1В том и другом случае, проекционная связь Прямая линия – кратчайшее расстояние между двумя точкамиЗадание прямой линии: Аналитическим способом Графическими способами Графические способы задания прямой линииB2B1С2С11способ. Изображением проекций отрезков прямых линий: A1B1, A2B2 XZYА2А1В2В12 способ. Координатами концов отрезка прямой, например: А(55,30,20), В(15,35,70)Лекция 2. Метод проецирования. 3 способ. Натуральной величиной отрезка прямой IABI и углами наклона (f и 4 способ. Задание прямой ее следамиСледом прямой линии называется точка пересечения прямой А1А2ZYXП1П3П2В1В2ZYВ1А2В2Построение следовТочка F - фронтальный след прямой АВ. УF=0Точка H - Правило построения следов прямойДля построения фронтального следа (М) прямой (а) необходимо продолжить Правило построения следов прямойДля построения горизонтального следа (N) прямой (а) необходимо продолжить Прямые в пространстве могут занимать общее и частное положениеПрямые общего положения не Прямые линии общего положенияа2в2с2а1в1с1Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии Прямые линии частного положения• прямые перпендикулярные плоскостям проекций - проецирующие прямые Прямые частного положения перпендикулярные плоскостям проекций 1. Проецирующие прямые Горизонтально-проецирующая прямая АB1А1B2А2BΞZXYZXYА1 Фронтально-проецирующая прямаяCYZXYXZDC1C1C2ΞD2C2Ξ D2D1D1CD ┴ П2I C1D1 I = I CD IОЛекция 2. Прямые частного положения параллельные плоскостям проекций 2. Прямые уровня горизонтальная прямая, фронтальная прямая, фронталь fXZYC2C1D2D1CD II П2 УС = YDIС2D2I = Определение натуральной величины отрезка прямой общего положения. Метод прямоугольного треуголькинаДЛИНА ОТРЕЗКА РАВНА АΞА1А2ZYXП1П3П2В1В2ZYВ1АΞА1А2В2ВZ = ZB – ZAВ*ΔZffВ*ΔZΔZXΔZА1В1IABIIABIЛекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линииМЕТОД ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА ΔY= YA- YBZYXВ1А2В2В*А1ΔYfА*yIАВ IIАВ II ΔY IЛекция 2. Метод проецирования. Ортогональный чертеж Относительное положение прямых1. Параллельно2. Перпендикулярно3. Пересекаться4. Скрещиваться Прямые в пространстве Параллельные прямыеПроекции параллельных прямых параллельныXZYа2a1b2b1a II b => a1 II b1 a Перпендикулярные прямыеXYZa2b2a1b1Oa II П1a ┴ b => a1 ┴ b1Лекция 2. Метод Пересекающиеся прямыеXZYa2К1b2b1a1К2a b =>a1 b1 =K1a b =>a2 Скрещивающиеся прямые Скрещивающиеся прямые лежат в разных плоскостях. Точки скрещивания Выводы по темеДля создания чертежа (эпюра) применяют ортогональное (прямоугольное) проецированиеПлоскости проекций в Выводы по темеПрямые подразделяются на прямые общего и частного положения относительно плоскостей Выводы по темеСпособом прямоугольного треугольника можно определить натуральную величину прямой общего положенияДве Список рекомендуемой литературыНачертательная геометрия: учеб. для студентов строит. специальностей вузов / [Н. Благодарю за вниманиеЛекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии
Слайды презентации

Слайд 2 Тема 2. Метод проецирования. Ортогональный чертеж точки и

Тема 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

прямой линии

Слайд 3 Цель и задачи лекции
Определить основы построения ортогонального чертежа
Дать

Цель и задачи лекцииОпределить основы построения ортогонального чертежаДать понятия октантов пространстваРаскрыть

понятия октантов пространства
Раскрыть сущность построения точки и прямой линии

в системе двух и трех плоскостей проекций

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 4 В результате изучения темы Вы будете знать
Виды проецирования

В результате изучения темы Вы будете знатьВиды проецирования в начертательной геометрииОртогональную

в начертательной геометрии
Ортогональную систему плоскостей и осей координат
Ортогональный чертеж

(эпюр) точки и прямой линии
Сущность способа прямоугольного треугольника

В результате изучения темы Вы будете уметь:
Строить и обозначать плоскости и оси координат
Выполнять эпюр точки и прямой линии


Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 5 - НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ -
занимается построением изображений и

- НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ -занимается построением изображений и изучением пространственных объектов

изучением пространственных объектов по их изображениям графическими методами

Лекция 2.

Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 6 Основные задачи начертательной геометрии
Создание – чертежа или эпюра

Основные задачи начертательной геометрииСоздание – чертежа или эпюра Решение задач на


Решение задач на плоскости
3. Создание пространственного объекта по

его изображению - чтение чертежа

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 7 Проецирование – процесс получения на чертеже достоверного изображения,

Проецирование – процесс получения на чертеже достоверного изображения, по которому

по которому можно представить форму и размеры объекта
Лекция 2.

Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 8
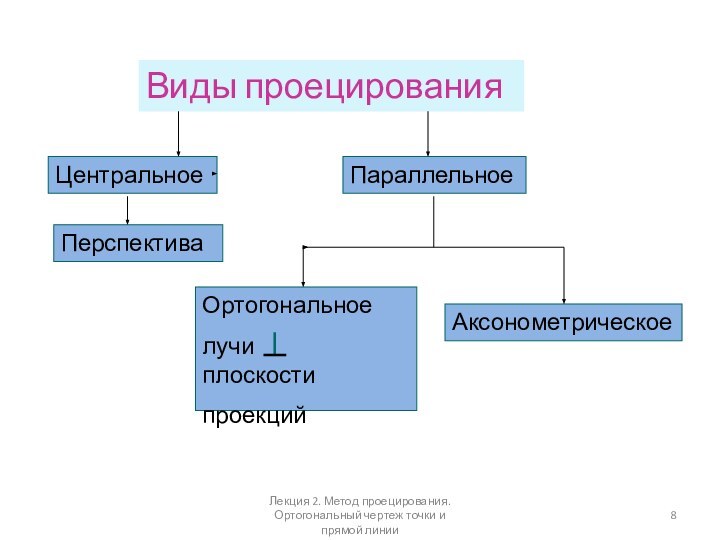
Виды проецирования
Центральное

Параллельное

Ортогональное
лучи плоскости
проекций

Виды проецированияЦентральноеПараллельноеОртогональноелучи плоскостипроекций АксонометрическоеПерспективаЛекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии




Аксонометрическое
Перспектива
Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой

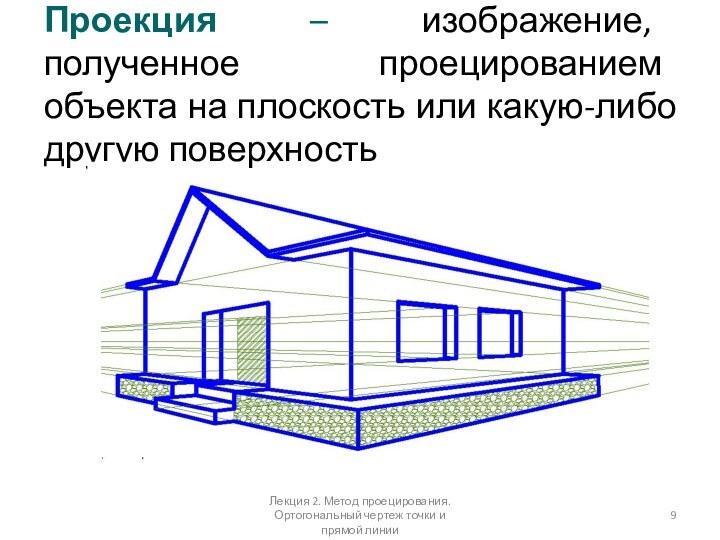
линии

Слайд 9 Проекция – изображение, полученное проецированием объекта на плоскость

Проекция – изображение, полученное проецированием объекта на плоскость или какую-либо другую

или какую-либо другую поверхность

Лекция 2. Метод проецирования. Ортогональный чертеж

точки и прямой линии

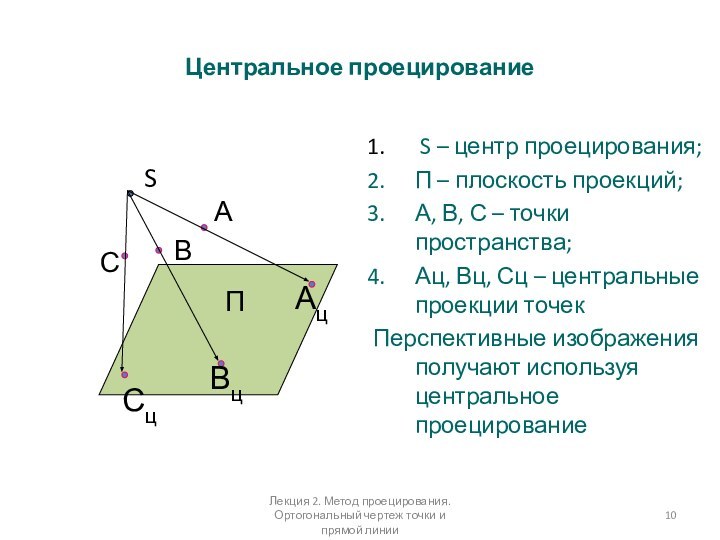
Слайд 10 S – центр проецирования;
П – плоскость проекций;
А,

S – центр проецирования;П – плоскость проекций;А, В, С –

В, С – точки пространства;
Ац, Вц, Сц – центральные

проекции точек
Перспективные изображения получают используя центральное проецирование

Центральное проецирование



S


А






П

В

С

Ац

Вц

Сц

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

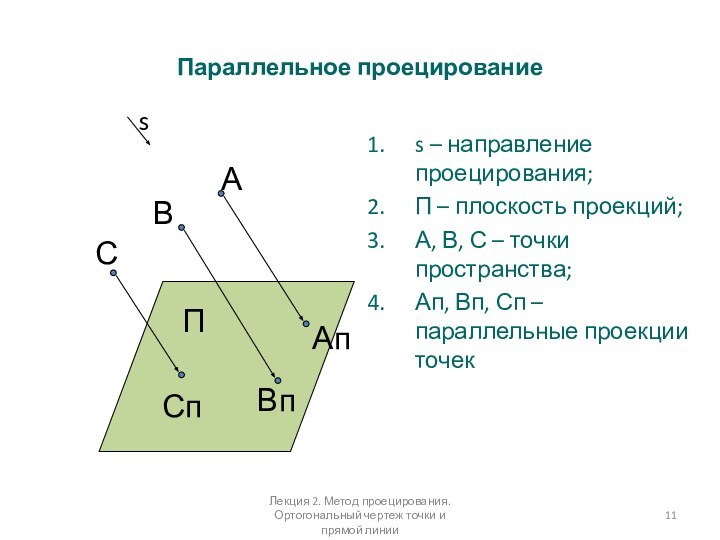
Слайд 11 Параллельное проецирование
s – направление проецирования;
П – плоскость проекций;
А,

Параллельное проецированиеs – направление проецирования;П – плоскость проекций;А, В, С –

В, С – точки пространства;
Ап, Вп, Сп – параллельные

проекции точек









Ап

Вп

Сп

С

В

А

П

s

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

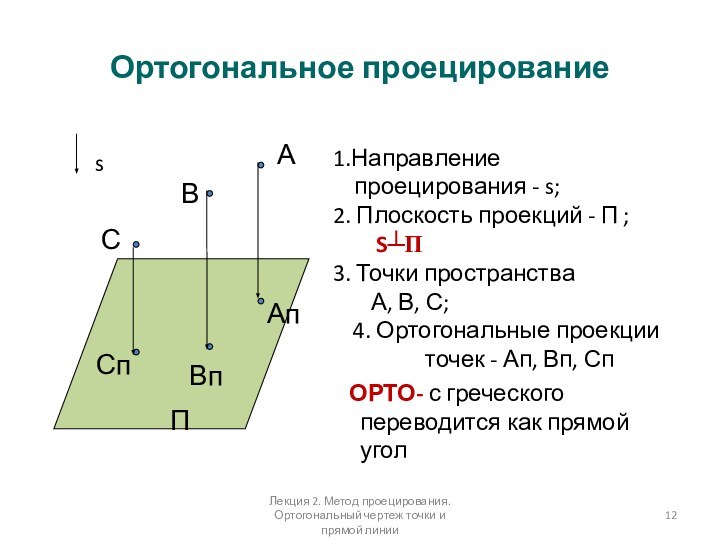
Слайд 12 Ортогональное проецирование







Вп
Сп
С
В
А
П
s
Ап
1.Направление
проецирования - s;
2. Плоскость

Ортогональное проецированиеВпСпСВАПsАп1.Направление проецирования - s;2. Плоскость проекций - П ;

проекций - П ;
S┴П
3. Точки

пространства
А, В, С;
4. Ортогональные проекции точек - Ап, Вп, Сп
ОРТО- с греческого переводится как прямой угол

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 13






Ап
Вп
Сп
С
В
А
П


S

А





П
В
С
Сп
Ап
Вп






Лекция 2. Метод проецирования. Ортогональный чертеж точки и

АпВпСпСВАПSАПВССпАпВпЛекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линииПараллельное и центральное проецирование

прямой линии
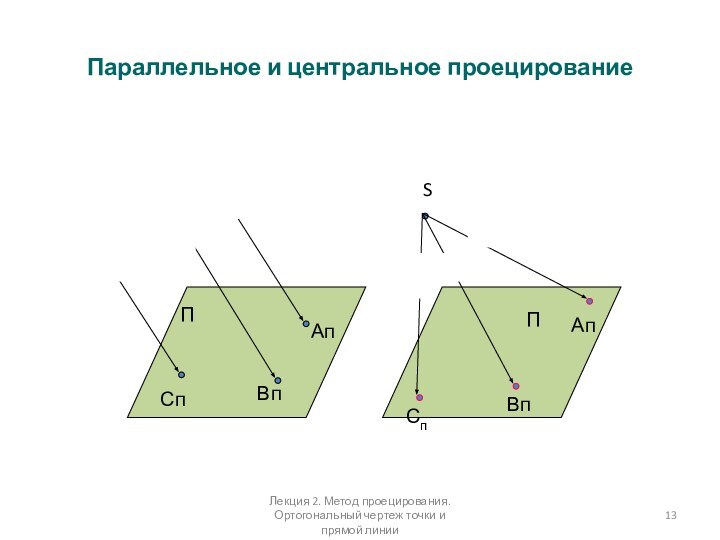
Параллельное и центральное проецирование

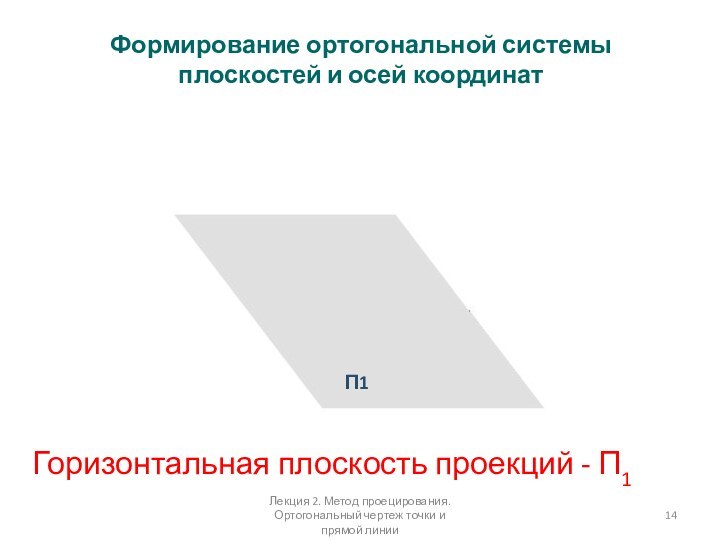
Слайд 14 Формирование ортогональной системы плоскостей и осей координат
П1
Горизонтальная плоскость

Формирование ортогональной системы плоскостей и осей координатП1Горизонтальная плоскость проекций - П1Лекция

проекций - П1
Лекция 2. Метод проецирования. Ортогональный чертеж точки

и прямой линии

Слайд 15 П2
П1
Горизонтальная плоскость проекций
Фронтальная плоскость проекций – П2

П2П1Горизонтальная плоскость проекцийФронтальная плоскость проекций – П2

Слайд 16
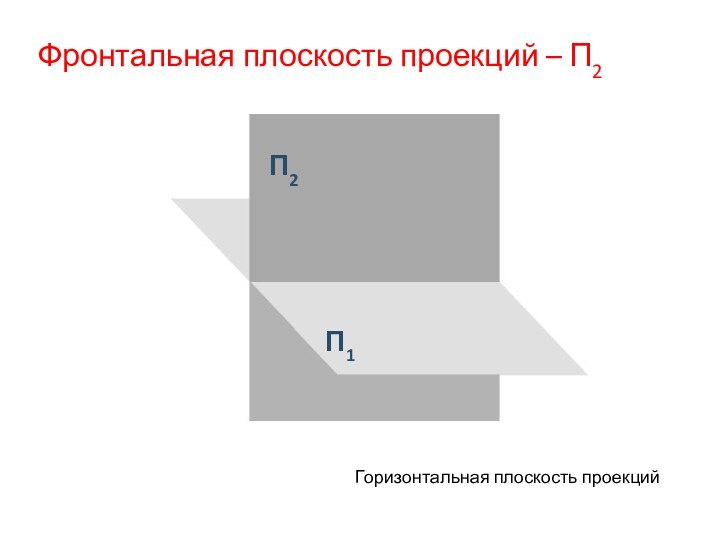
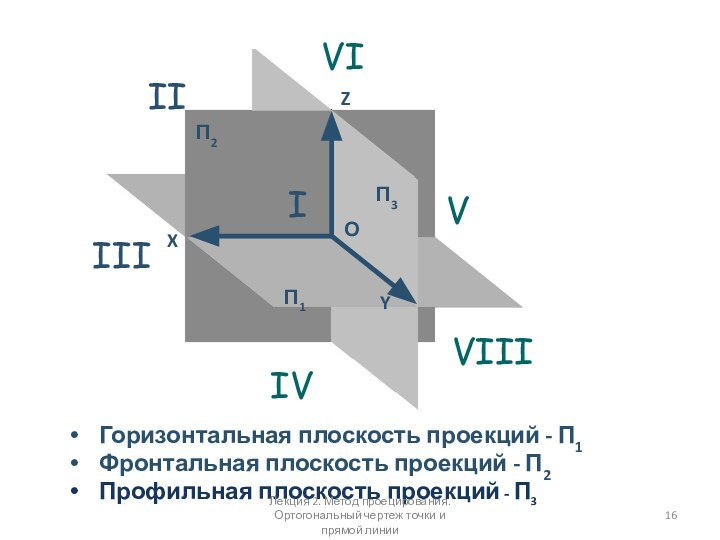
Горизонтальная плоскость проекций - П1
Фронтальная

Горизонтальная плоскость проекций - П1 Фронтальная плоскость проекций - П2

плоскость проекций - П2
Профильная плоскость проекций

- П3

П2

П1

П3

X

Z

Y

О

І

ІI


ІII

IV

V

VI

VIII

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

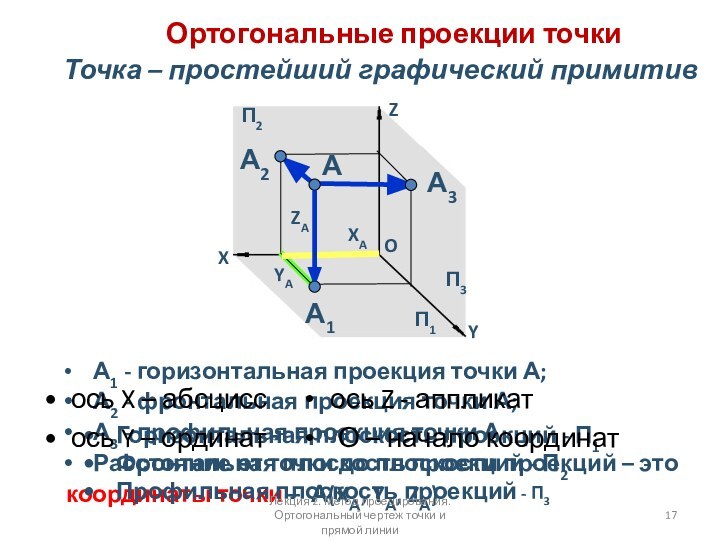
Слайд 17 Ортогональные проекции точки
А1 - горизонтальная проекция точки

Ортогональные проекции точки А1 - горизонтальная проекция точки А; А2 -

А;
А2 - фронтальная проекция точки А;
А3 -

профильная проекция точки А.
Расстояние от точки до плоскости проекций – это
координаты точки – А(XА, YА, ZА)

X

Y

O

П1

П3

П2

XA

Z

А

А1

А2

А3

YA

ZA





Точка – простейший графический примитив


Горизонтальная плоскость проекций - П1
Фронтальная плоскость проекций - П2
Профильная плоскость проекций - П3

ось X – абсцисс • ось Z - аппликат
ось Y – ординат • О – начало координат

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

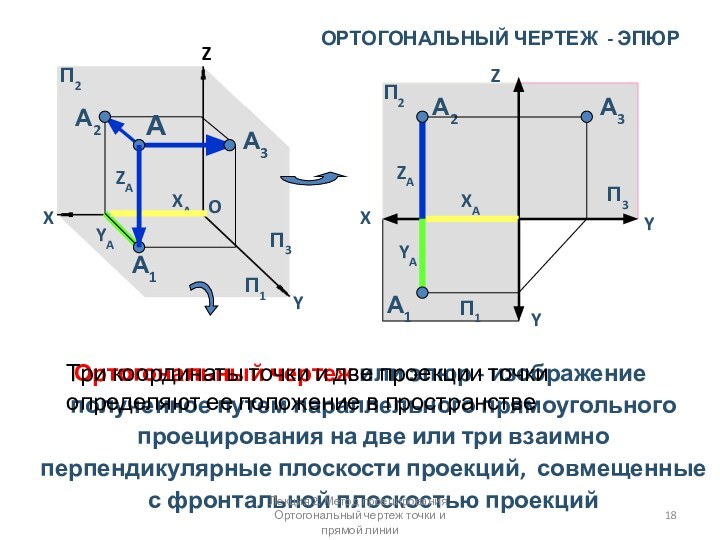
Слайд 18 ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ - ЭПЮР
Ортогональный чертеж или эпюр -

ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ - ЭПЮРОртогональный чертеж или эпюр - изображение полученное путем

изображение полученное путем параллельного прямоугольного проецирования на две или

три взаимно перпендикулярные плоскости проекций, совмещенные с фронтальной плоскостью проекций




Z

Y

Y

X

П3

П1

П2

XA

А2




А3

YA

ZA

X

Y

O

П1

П3

П2

XA


Z

А

А1

А2

А3

YA

ZA


А1





Три координаты точки и две проекции точки определяют ее положение в пространстве

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

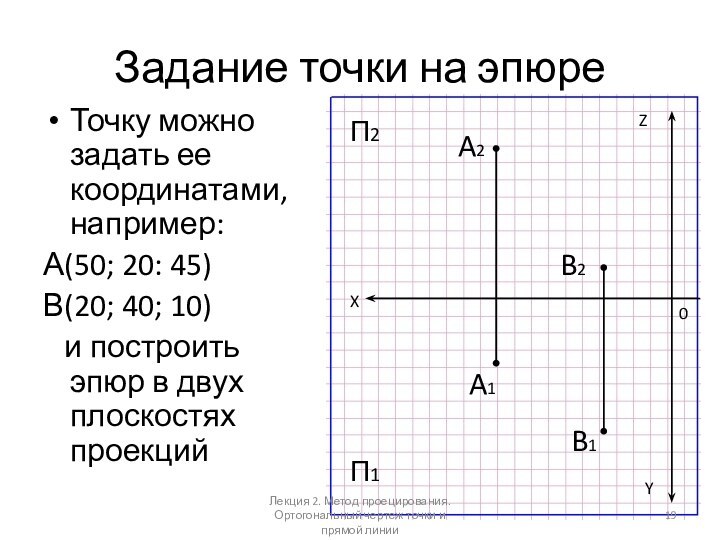
Слайд 19 Задание точки на эпюре
Точку можно задать ее координатами,

Задание точки на эпюреТочку можно задать ее координатами, например:А(50; 20: 45)В(20;

например:
А(50; 20: 45)
В(20; 40; 10)
и построить эпюр

в двух плоскостях проекций

X

Z

Y

0

A1

A2

B2

B1

П1

П2

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

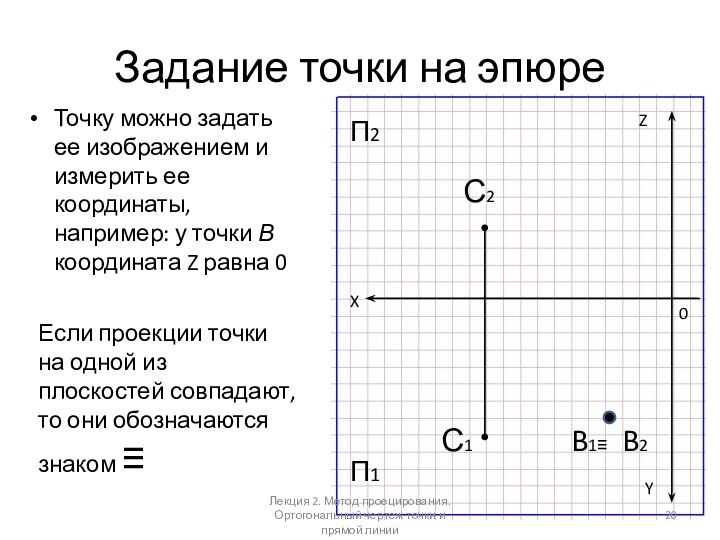
Слайд 20 Задание точки на эпюре
Точку можно задать ее изображением

Задание точки на эпюреТочку можно задать ее изображением и измерить ее

и измерить ее координаты, например: у точки В координата

Z равна 0

X

Z

Y

0

С1

С2

B2

B1≡

П1

П2


Если проекции точки на одной из плоскостей совпадают, то они обозначаются знаком ≡

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

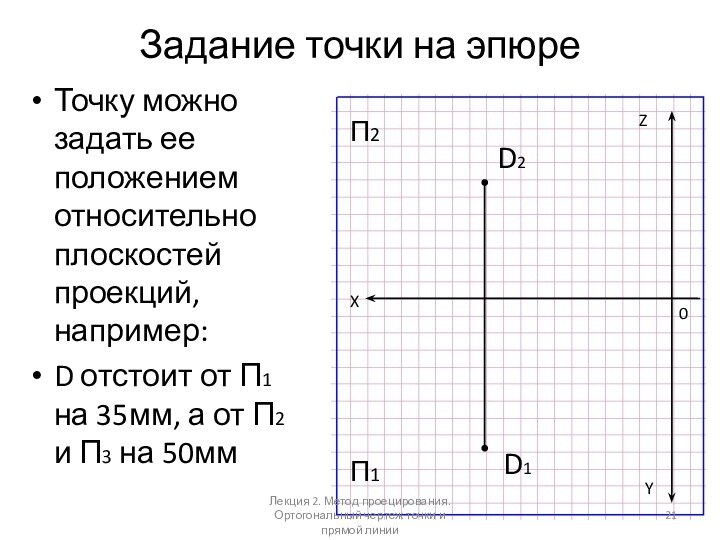
Слайд 21 Задание точки на эпюре
Точку можно задать ее положением

Задание точки на эпюреТочку можно задать ее положением относительно плоскостей проекций,

относительно плоскостей проекций, например:
D отстоит от П1 на 35мм,

а от П2 и П3 на 50мм

X

Z

Y

0

D1

D2

П1

П2

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

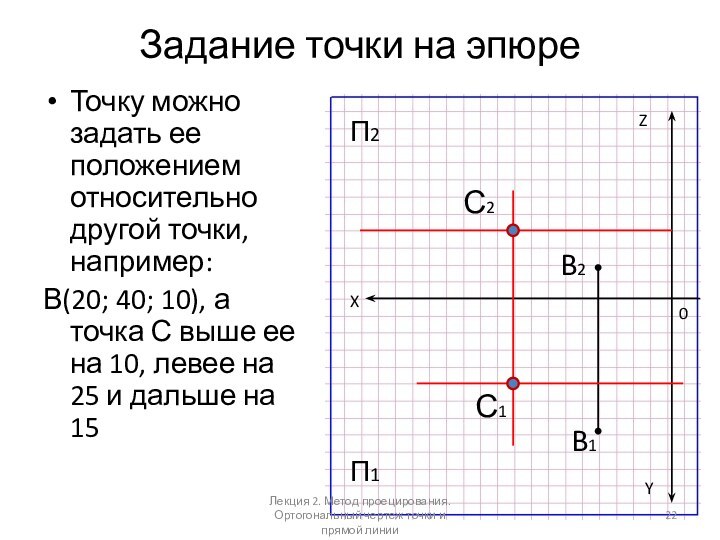
Слайд 22 Задание точки на эпюре
Точку можно задать ее положением

Задание точки на эпюреТочку можно задать ее положением относительно другой точки,

относительно другой точки, например:
В(20; 40; 10), а точка С

выше ее на 10, левее на 25 и дальше на 15

X

Z

Y

0

B2

B1

П1

П2



С2

С1

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

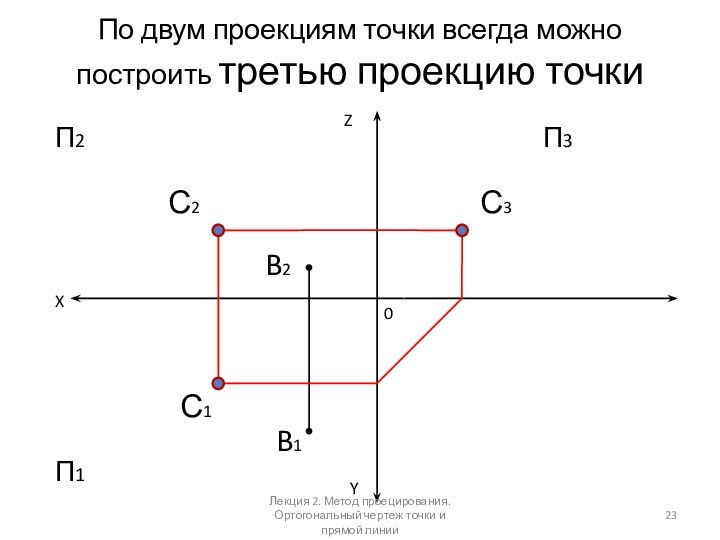
Слайд 23 По двум проекциям точки всегда можно построить третью

По двум проекциям точки всегда можно построить третью проекцию точкиXZY0B2B1П1П2С2С1С3П3Лекция 2.

проекцию точки
X
Z
Y
0
B2
B1
П1
П2


С2
С1

С3
П3
Лекция 2. Метод проецирования. Ортогональный чертеж точки и

прямой линии

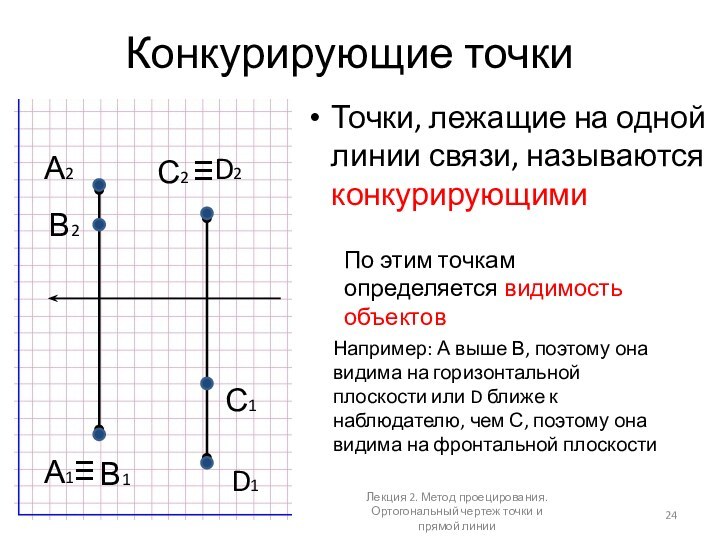
Слайд 24 Конкурирующие точки
Точки, лежащие на одной линии связи, называются

Конкурирующие точкиТочки, лежащие на одной линии связи, называются конкурирующимиА2А1≡В1В2С2 ≡С1D1D2Лекция 2.

конкурирующими
А2
А1≡
В1
В2





С2 ≡
С1

D1
D2
Лекция 2. Метод проецирования. Ортогональный чертеж точки и

прямой линии

Например: А выше В, поэтому она видима на горизонтальной плоскости или D ближе к наблюдателю, чем С, поэтому она видима на фронтальной плоскости

По этим точкам определяется видимость объектов

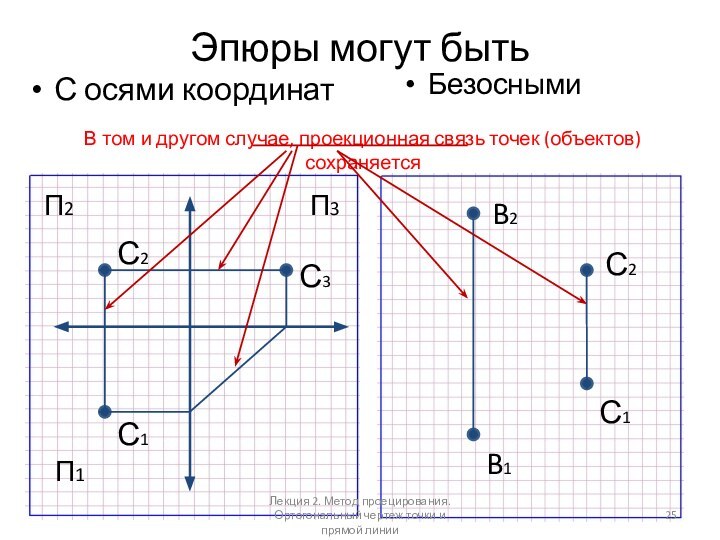
Слайд 25 Эпюры могут быть
С осями координат
Безосными







B2
B1
П1
П2
С2
С1
С3
П3
С2
С1
В том и

Эпюры могут бытьС осями координатБезосными B2B1П1П2С2С1С3П3С2С1В том и другом случае, проекционная

другом случае, проекционная связь точек (объектов) сохраняется
Лекция 2. Метод

проецирования. Ортогональный чертеж точки и прямой линии

Слайд 26 Прямая линия – кратчайшее расстояние между двумя точками
Задание

Прямая линия – кратчайшее расстояние между двумя точкамиЗадание прямой линии: Аналитическим способом Графическими способами

прямой линии:
Аналитическим способом
Графическими способами

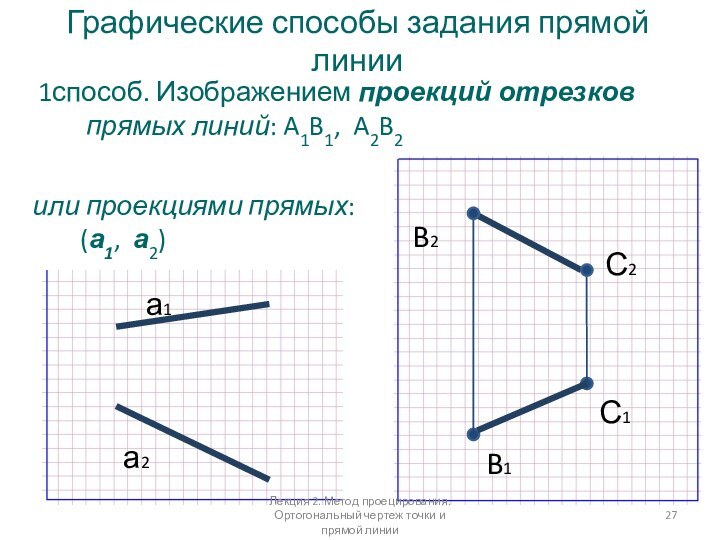
Слайд 27 Графические способы задания прямой линии


B2
B1
С2
С1
1способ. Изображением проекций отрезков

Графические способы задания прямой линииB2B1С2С11способ. Изображением проекций отрезков прямых линий: A1B1,

прямых линий: A1B1, A2B2


или проекциями прямых: (а1, а2)


а1

а2

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 28

X
Z
Y
А2
А1
В2
В1




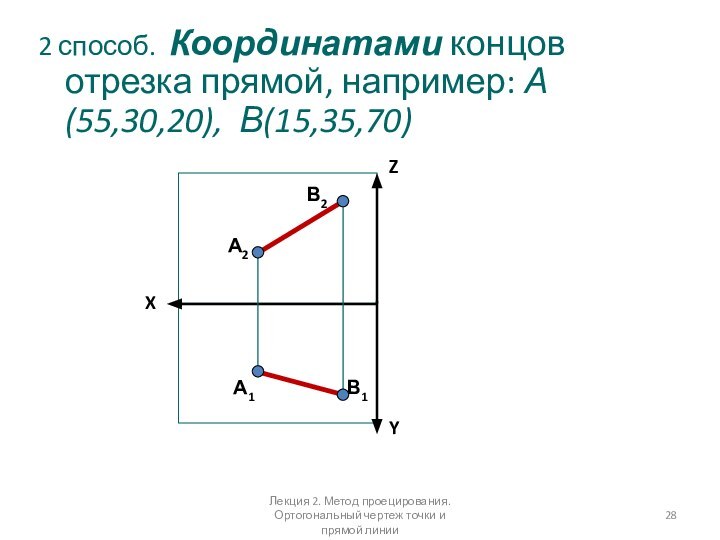
2 способ. Координатами концов отрезка прямой, например: А(55,30,20),

XZYА2А1В2В12 способ. Координатами концов отрезка прямой, например: А(55,30,20), В(15,35,70)Лекция 2. Метод

В(15,35,70)
Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой

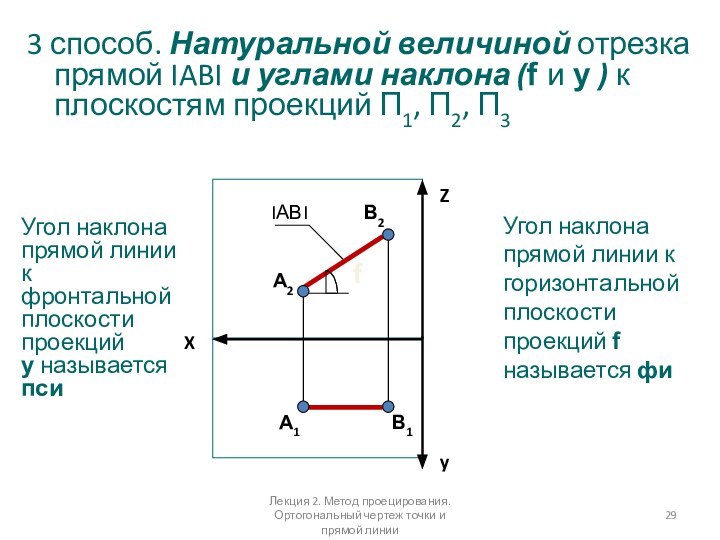
линии

Слайд 29 3 способ. Натуральной величиной отрезка прямой IABI и

3 способ. Натуральной величиной отрезка прямой IABI и углами наклона (f

углами наклона (f и y ) к плоскостям проекций

П1, П2, П3



X

Z

А2

А1

В2

В1






f

y

IАВI

Угол наклона прямой линии к горизонтальной плоскости проекций f называется фи

Угол наклона прямой линии к фронтальной плоскости проекций
y называется пси

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 30 4 способ. Задание прямой ее следами
Следом прямой линии

4 способ. Задание прямой ее следамиСледом прямой линии называется точка пересечения

называется точка пересечения прямой с плоскостью проекций
У прямой линии

может быть три следа, которые образуются при пересечении с горизонтальной, фронтальной и профильной плоскостями

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 31 А1
А2
Z
Y
X
П1
П3
П2
В1
В2
Z
Y
В1
А2
В2

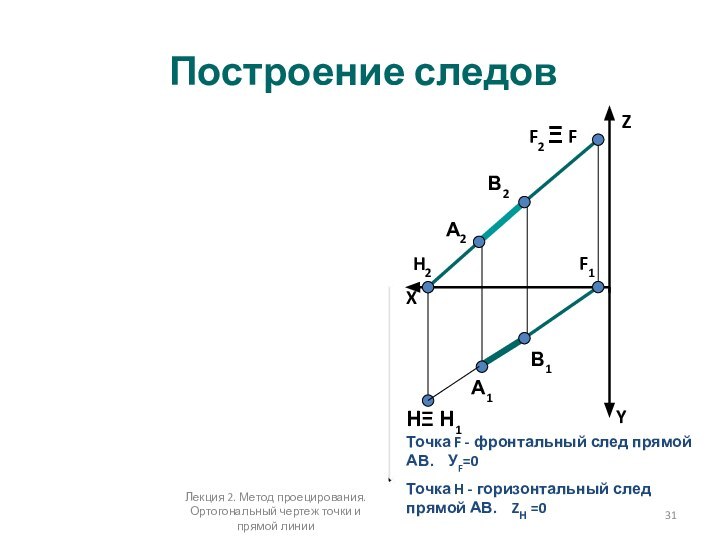
Построение следов
Точка F - фронтальный след прямой АВ.

А1А2ZYXП1П3П2В1В2ZYВ1А2В2Построение следовТочка F - фронтальный след прямой АВ. УF=0Точка H -

УF=0
Точка H - горизонтальный след прямой АВ.

ZН =0

А1

X















А

B

H1ΞH

F2ΞF


H2


F1


F2 Ξ F


F1

H2

HΞ H1

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

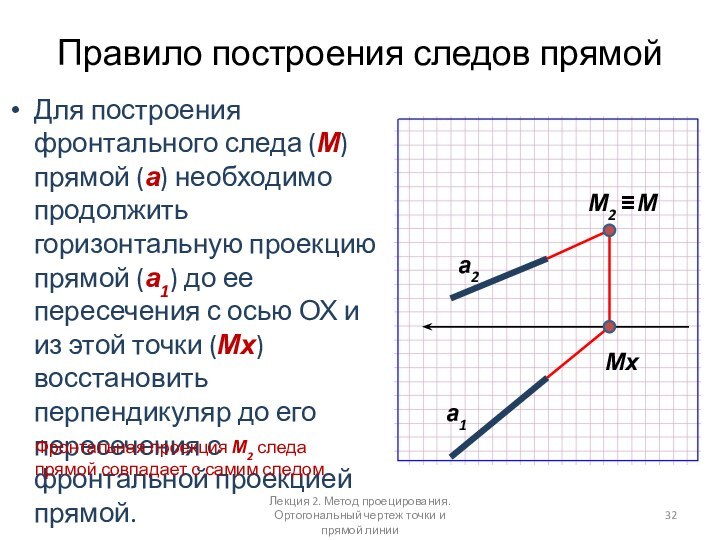
Слайд 32 Правило построения следов прямой
Для построения фронтального следа (М)

Правило построения следов прямойДля построения фронтального следа (М) прямой (а) необходимо

прямой (а) необходимо продолжить горизонтальную проекцию прямой (а1) до

ее пересечения с осью ОХ и из этой точки (Мх) восстановить перпендикуляр до его пересечения с фронтальной проекцией прямой.



а2

а1

М2 ≡ М

Мх

Фронтальная проекция М2 следа прямой совпадает с самим следом

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

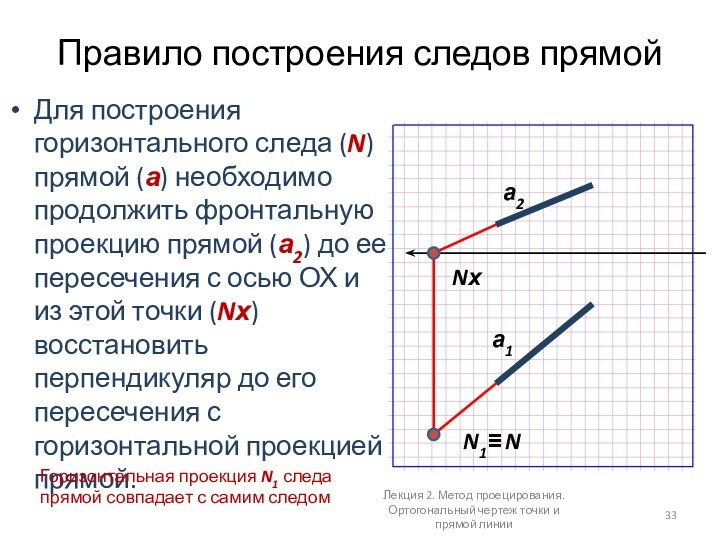
Слайд 33 Правило построения следов прямой
Для построения горизонтального следа (N)

Правило построения следов прямойДля построения горизонтального следа (N) прямой (а) необходимо

прямой (а) необходимо продолжить фронтальную проекцию прямой (а2) до

ее пересечения с осью ОХ и из этой точки (Nх) восстановить перпендикуляр до его пересечения с горизонтальной проекцией прямой.



а2

а1

N1≡ N

Nх

Горизонтальная проекция N1 следа прямой совпадает с самим следом

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 34 Прямые в пространстве могут занимать общее и частное

Прямые в пространстве могут занимать общее и частное положениеПрямые общего положения

положение
Прямые общего положения не параллельны и не перпендикулярны ни

одной из плоскостей проекций

Прямые частного положения либо параллельны, либо перпендикулярны плоскостям проекций

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

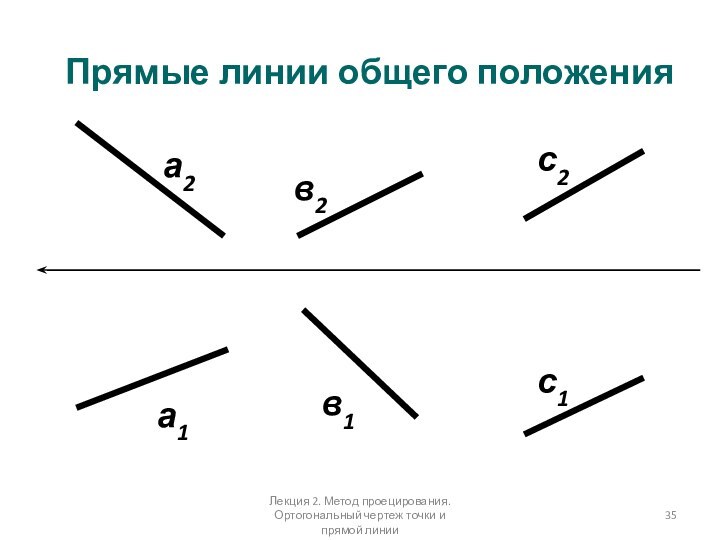
Слайд 35 Прямые линии общего положения
а2
в2
с2
а1
в1
с1
Лекция 2. Метод проецирования.

Прямые линии общего положенияа2в2с2а1в1с1Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Ортогональный чертеж точки и прямой линии

Слайд 36 Прямые линии частного положения
• прямые перпендикулярные плоскостям проекций

Прямые линии частного положения• прямые перпендикулярные плоскостям проекций - проецирующие прямые

- проецирующие прямые


• прямые параллельные плоскостям

проекций – линии уровня

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

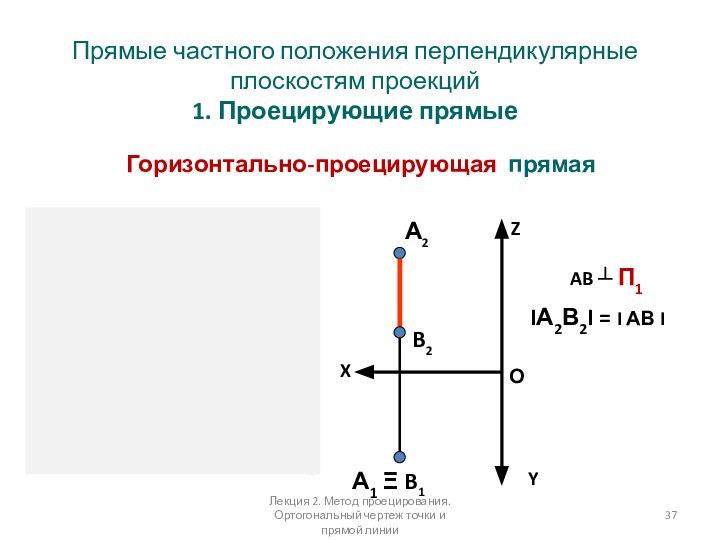
Слайд 37 Прямые частного положения перпендикулярные плоскостям проекций 1. Проецирующие прямые

Прямые частного положения перпендикулярные плоскостям проекций 1. Проецирующие прямые Горизонтально-проецирующая прямая


Горизонтально-проецирующая прямая





А
B1
А1
B2
А2
B
Ξ
Z
X
Y
Z
X
Y


А1 Ξ B1
B2
А2

О
О
AB ┴ П1
IА2В2I

= I АВ I



Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 38 Фронтально-проецирующая прямая










C
Y
Z
X
Y
X
Z
D
C1
C1
C2ΞD2
C2
Ξ D2
D1
D1
CD ┴ П2
I C1D1 I =

Фронтально-проецирующая прямаяCYZXYXZDC1C1C2ΞD2C2Ξ D2D1D1CD ┴ П2I C1D1 I = I CD IОЛекция

I CD I

О

Лекция 2. Метод проецирования. Ортогональный чертеж точки

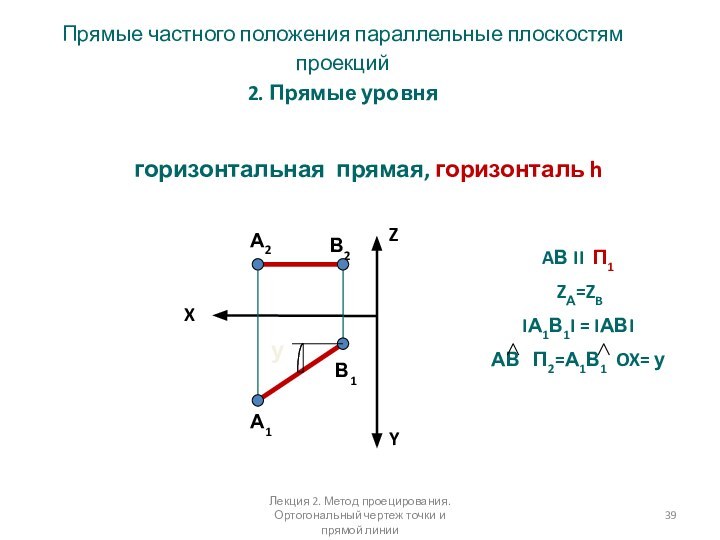
и прямой линии

Слайд 39 Прямые частного положения параллельные плоскостям проекций 2. Прямые

Прямые частного положения параллельные плоскостям проекций 2. Прямые уровня горизонтальная прямая,

уровня
горизонтальная прямая, горизонталь h
X
Z
Y
А2
А1
В2
В1




AВ II П1

ZА=ZB
IА1В1I = IАВI
АВ П2=А1В1 OX= y


y

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

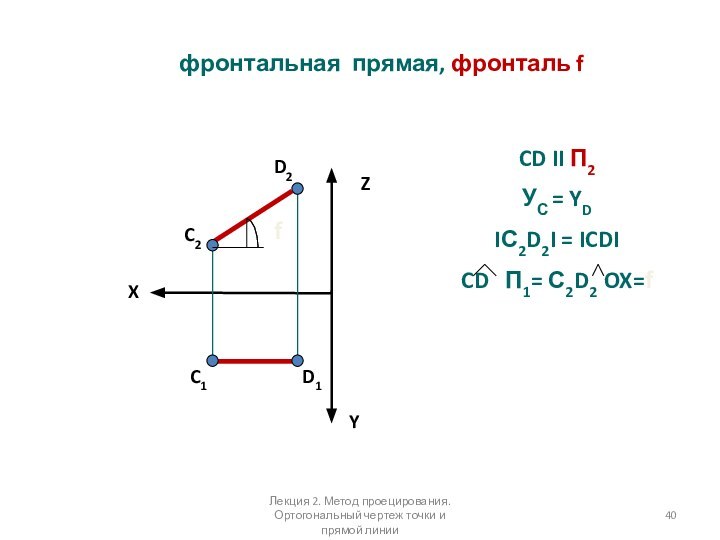
Слайд 40 фронтальная прямая, фронталь f

X
Z
Y
C2
C1
D2
D1




CD II П2

фронтальная прямая, фронталь fXZYC2C1D2D1CD II П2 УС = YDIС2D2I =


УС = YD
IС2D2I = ICDI
CD П1= С2D2 OX=f

f
Лекция

2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 41 Определение натуральной величины отрезка прямой общего положения. Метод

Определение натуральной величины отрезка прямой общего положения. Метод прямоугольного треуголькинаДЛИНА ОТРЕЗКА

прямоугольного треуголькина
ДЛИНА ОТРЕЗКА РАВНА
ГИПОТЕНУЗЕ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
ОДИН КАТЕТ

КОТОРОГО РАВЕН ПРОЕКЦИИ
ОТРЕЗКА,
А ДРУГОЙ – РАЗНОСТИ КООРДИНАТ КОНЦОВ
ОТРЕЗКА ОТ ЭТОЙ ЖЕ ПЛОСКОСТИ

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

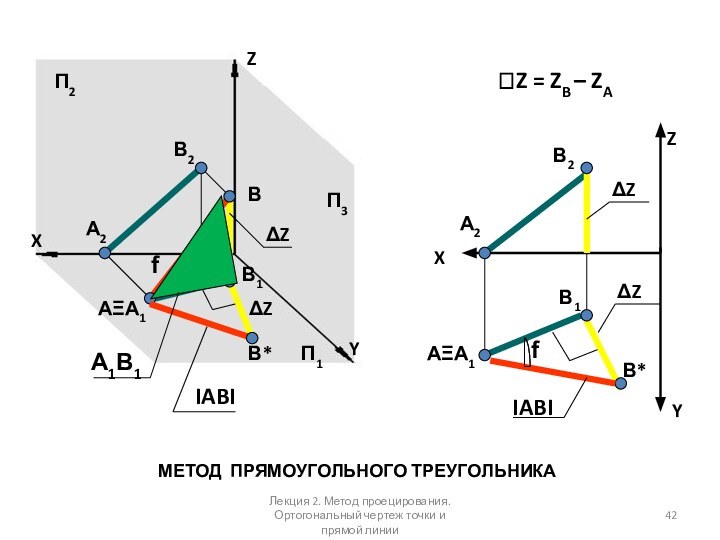
Слайд 42 АΞА1
А2
Z
Y
X
П1
П3
П2
В1
В2
Z
Y
В1
АΞА1
А2
В2




В

Z = ZB – ZA

В*




ΔZ


f
f
В*


ΔZ
ΔZ
X
ΔZ


А1В1
IABI
IABI
Лекция 2. Метод проецирования.

АΞА1А2ZYXП1П3П2В1В2ZYВ1АΞА1А2В2ВZ = ZB – ZAВ*ΔZffВ*ΔZΔZXΔZА1В1IABIIABIЛекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линииМЕТОД ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА

Ортогональный чертеж точки и прямой линии
МЕТОД ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА

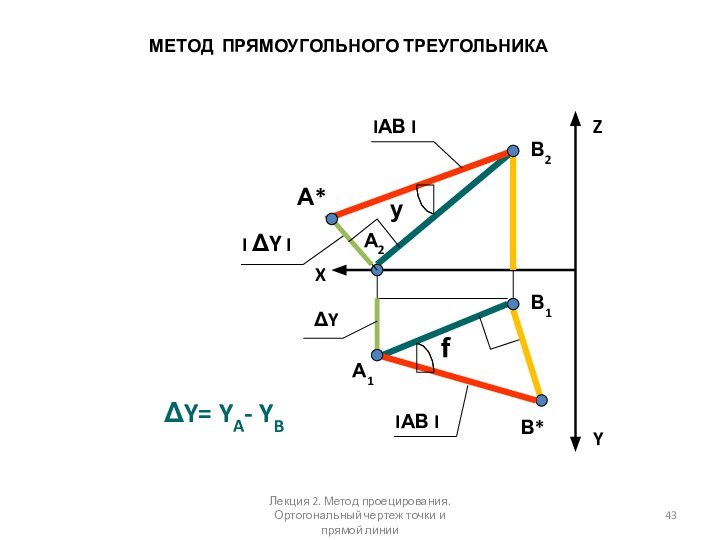
Слайд 43 ΔY= YA- YB
Z
Y
X
В1
А2
В2

В*


А1
ΔY

f
А*


y


IАВ I
IАВ I
I ΔY I
Лекция 2.

ΔY= YA- YBZYXВ1А2В2В*А1ΔYfА*yIАВ IIАВ II ΔY IЛекция 2. Метод проецирования. Ортогональный

Метод проецирования. Ортогональный чертеж точки и прямой линии
МЕТОД ПРЯМОУГОЛЬНОГО

ТРЕУГОЛЬНИКА

Слайд 44 Относительное положение прямых
1. Параллельно

2. Перпендикулярно

3. Пересекаться

4. Скрещиваться




Относительное положение прямых1. Параллельно2. Перпендикулярно3. Пересекаться4. Скрещиваться Прямые в пространстве


Прямые в пространстве могут быть расположены:
Лекция 2. Метод

проецирования. Ортогональный чертеж точки и прямой линии

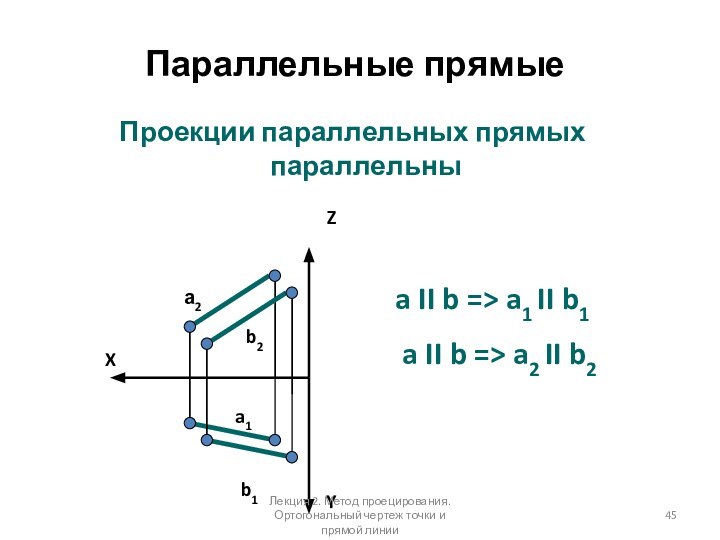
Слайд 45 Параллельные прямые
Проекции параллельных прямых параллельны
X
Z
Y
а2
a1








b2
b1
a II b =>

Параллельные прямыеПроекции параллельных прямых параллельныXZYа2a1b2b1a II b => a1 II b1

a1 II b1
a II b => a2 II

b2

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

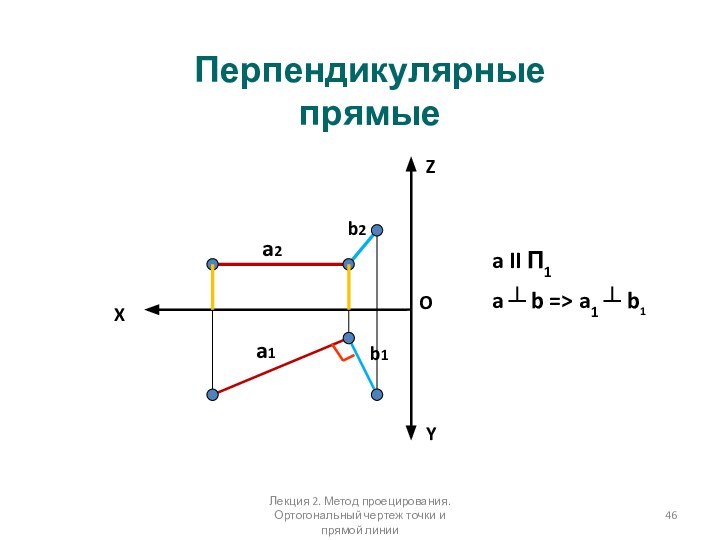
Слайд 46 Перпендикулярные прямые






X
Y
Z
a2
b2
a1
b1
O
a II П1
a ┴ b => a1

Перпендикулярные прямыеXYZa2b2a1b1Oa II П1a ┴ b => a1 ┴ b1Лекция 2.

┴ b1
Лекция 2. Метод проецирования. Ортогональный чертеж точки и

прямой линии

Слайд 47 Пересекающиеся прямые
X
Z
Y
a2
К1
b2
b1


a1
К2
a b =>a1 b1 =K1
a

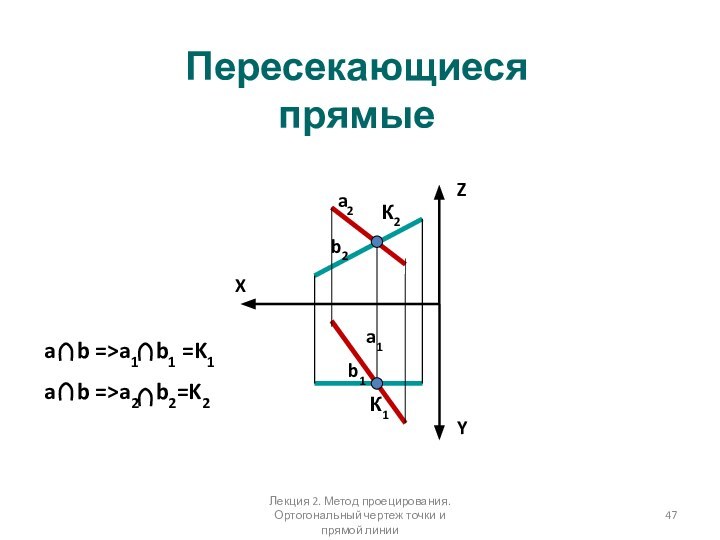
Пересекающиеся прямыеXZYa2К1b2b1a1К2a b =>a1 b1 =K1a b =>a2 b2=K2Лекция 2. Метод

b =>a2 b2=K2





Лекция 2. Метод проецирования. Ортогональный

чертеж точки и прямой линии

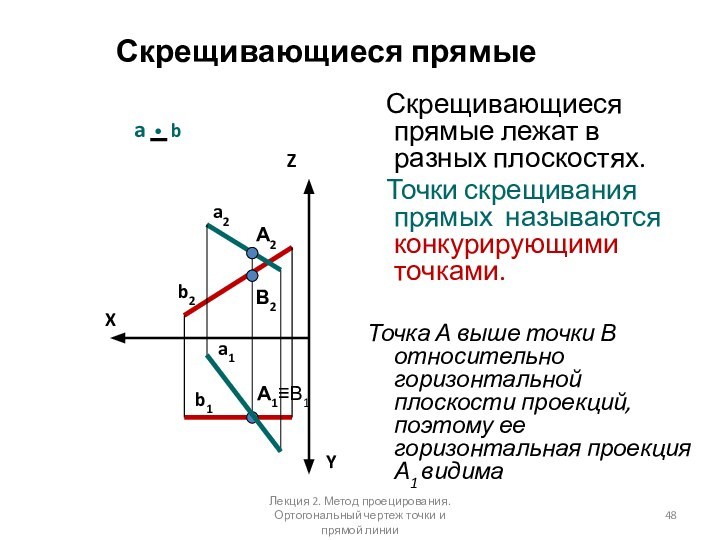
Слайд 48 Скрещивающиеся прямые
Скрещивающиеся прямые лежат в разных

Скрещивающиеся прямые Скрещивающиеся прямые лежат в разных плоскостях. Точки скрещивания

плоскостях.
Точки скрещивания прямых называются конкурирующими точками.


Точка А выше точки В относительно горизонтальной плоскости проекций, поэтому ее горизонтальная проекция А1 видима

X

Z

Y

a1

a2

b1



b2


А1≡В1

В2

А2

a • b

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 49 Выводы по теме
Для создания чертежа (эпюра) применяют ортогональное

Выводы по темеДля создания чертежа (эпюра) применяют ортогональное (прямоугольное) проецированиеПлоскости проекций

(прямоугольное) проецирование
Плоскости проекций в ортогональной системе три (горизонтальная –

П1, фронтальная – П2, профильная – П3
Эпюр точки можно построить по координатам (x, y, z) или по проекциям точки
Через две точки можно провести одну прямую линию

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 50 Выводы по теме
Прямые подразделяются на прямые общего и

Выводы по темеПрямые подразделяются на прямые общего и частного положения относительно

частного положения относительно плоскостей проекций
Прямые частного положения либо перпендикулярны,

либо параллельны плоскостям проекций
Прямая общего положения не параллельна и не перпендикулярна плоскостям проекций

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 51 Выводы по теме
Способом прямоугольного треугольника можно определить натуральную

Выводы по темеСпособом прямоугольного треугольника можно определить натуральную величину прямой общего

величину прямой общего положения
Две прямые в пространстве могут быть

расположены параллельно, перпендикулярно, пересекаться и скрещиваться

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

Слайд 52 Список рекомендуемой литературы
Начертательная геометрия: учеб. для студентов строит.

Список рекомендуемой литературыНачертательная геометрия: учеб. для студентов строит. специальностей вузов /

специальностей вузов / [Н. Н. Крылов, Г. С. Иконникова,

В. Л. Николаев, В. Е. Васильев] ; под ред. Н. Н. Крылова. - Изд. 11-е, стер. - Москва: Высшая школа, 2010. - 224 с.
Короев, Юрий Ильич. Начертательная геометрия: учебник для студентов архитектур. специальностей вузов / Ю. И. Короев. - 2-е изд., перераб. и доп. - Москва: Архитектура-С, 2007. - 424 с.

Лекция 2. Метод проецирования. Ортогональный чертеж точки и прямой линии

  • Имя файла: metod-proetsirovaniya-ortogonalnyy-chertezh-tochki-i-pryamoy-linii.pptx
  • Количество просмотров: 180
  • Количество скачиваний: 0
- Предыдущая История города Ростов-на-Дону
Следующая - Введение в психотерапию

Похожие презентации

Интерьер Интерьер 212
Виды, разрезы, сечения Виды, разрезы, сечения 182
Способы преобразования проекций (Лекция 3) Способы преобразования проекций (Лекция 3) 191
Виды чертежей Виды чертежей 200
Тени Тени 208
ГОСТ 2.109-73. Основные требования к чертежам ГОСТ 2.109-73. Основные требования к чертежам 204
Соединение вида и разреза Соединение вида и разреза 182
Проецирование. Виды Проецирование. Виды 194
Сборочный чертеж и деталирование сборочной единицы Сборочный чертеж и деталирование сборочной единицы 185
Лабораторная работа: Параметрические чертежи Лабораторная работа: Параметрические чертежи 182
Виды проецирования Виды проецирования 200
Кривые линии Кривые линии 180
Линия. Понятия и определения Линия. Понятия и определения 204
Размеры конструктивных элементов. Размеры детали Размеры конструктивных элементов. Размеры детали 275
Геометрические построения, необходимые при выполнении чертежей Геометрические построения, необходимые при выполнении чертежей 202
Перспектива – вид центральной проекции Перспектива – вид центральной проекции 223
Графика Графика 244
Черчение - Разрезы Черчение - Разрезы 190
Методологические основы и традиционные методы технического проектирования и конструирования Методологические основы и традиционные методы технического проектирования и конструирования 198
Сборочный чертеж Сборочный чертеж 274
Методы выполнения чертежей Методы выполнения чертежей 194
Геометрические построения Геометрические построения 193
План участка контрольного пункта автосцепки (КПА) с расстановкой оборудования План участка контрольного пункта автосцепки (КПА) с расстановкой оборудования 172
Чертежи: план и разрез здания Чертежи: план и разрез здания 187
Разрезы. Назначение и виды Разрезы. Назначение и виды 252
Построение проекции точек на поверхности геометрических тел Построение проекции точек на поверхности геометрических тел 217
Чертёж. Что это? Чертёж. Что это? 193
Технический рисунок Технический рисунок 199
Общие правила выполнения чертежей Общие правила выполнения чертежей 204
Тень от поверхности. Тени от геометрических тел Тень от поверхности. Тени от геометрических тел 275