- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Построение проекции точек на поверхности геометрических тел
Содержание
- 2. Задание 1: напишите номера видов сверху, которые соответствуют главному виду
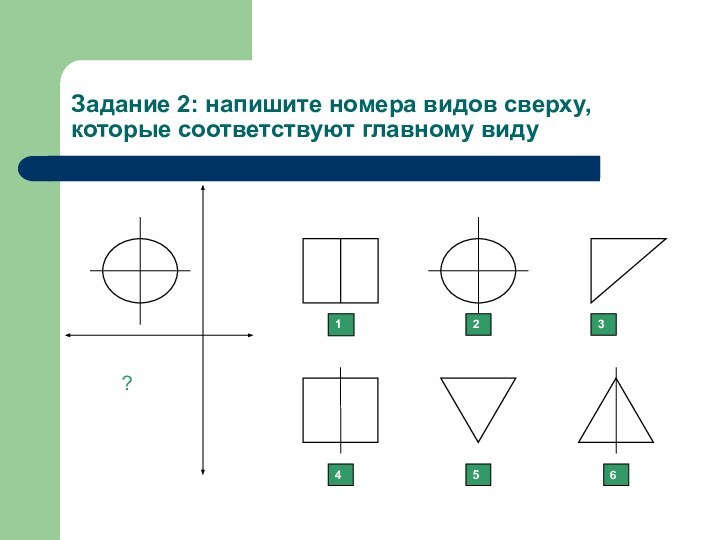
- 3. Задание 2: напишите номера видов сверху, которые соответствуют главному виду
- 4. Геометрические тела105678923Разделите геометрические тела на многогранники и тела вращения14
- 5. Геометрические тела11056789243Многогранники Тела вращения
- 6. Классификация геометрических телгеометрические теламногогранникитела вращенияпризмапирамидацилиндрконусшартор
- 7. Построение проекций точки, лежащей на поверхности предмета
- 8. Элементы поверхности предметаГраниКривая поверхностьГрани – плоскости, которые составляют поверхности многогранника.
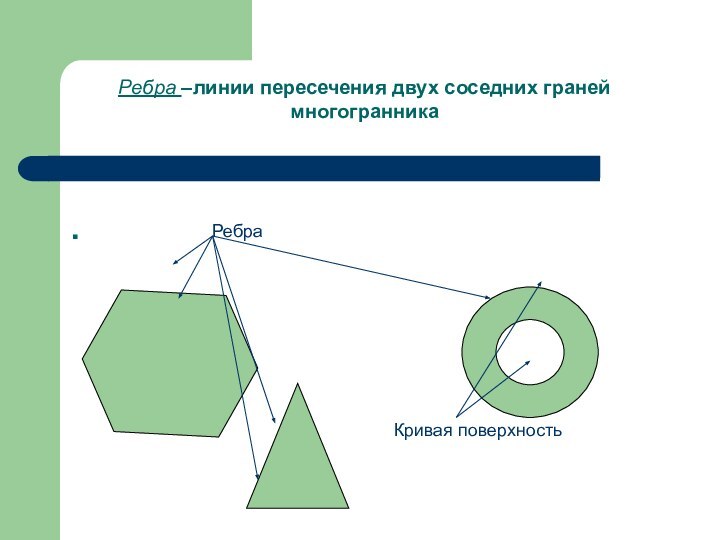
- 9. . РебраКривая поверхностьРебра –линии пересечения двух соседних граней многогранника
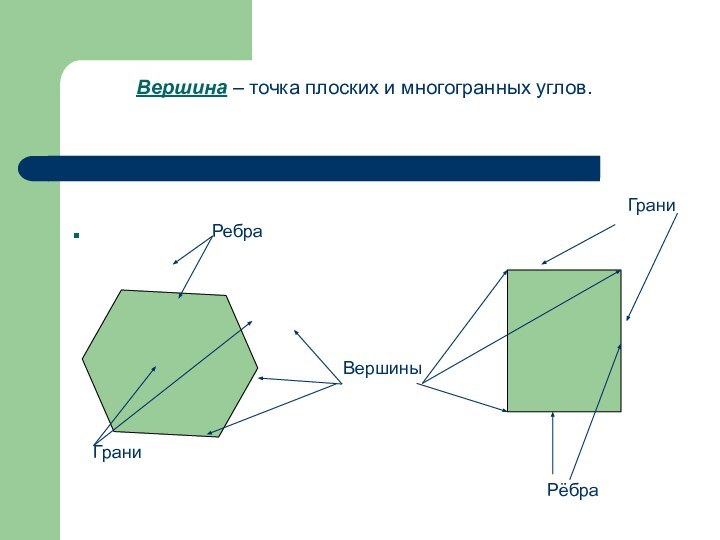
- 10. . РебраГраниВершиныВершина – точка плоских и многогранных углов. ГраниРёбра
- 11. Построение проекций точекЧтобы задать на чертеже проекции
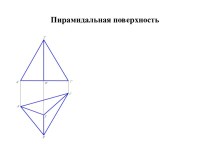
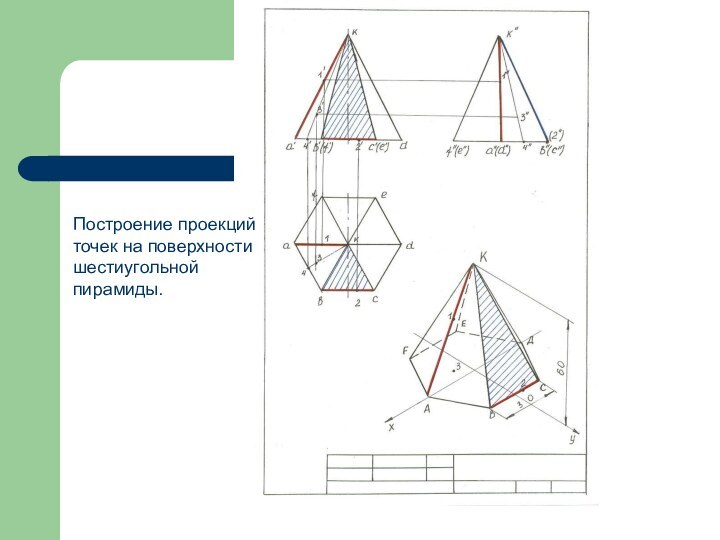
- 12. Построение проекций точек на поверхности шестиугольной пирамиды.
- 13. На первый взгляд — парадокс: вместо точки
- 14. Построение проекций точек на поверхности конусаНа рис.87
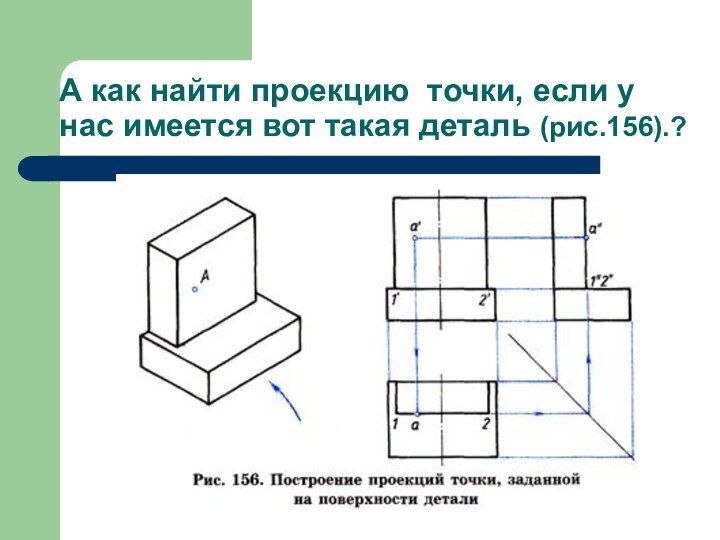
- 15. А как найти проекцию точки, если у нас имеется вот такая деталь (рис.156).?
- 16. Алгоритм построения проекции точкиАнализ геометрической формы предмета
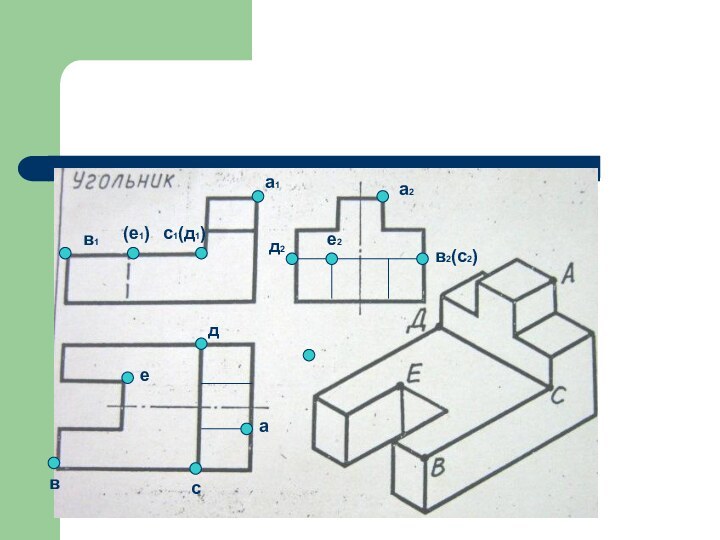
- 17. НАЙТИ НЕДОСТАЮЩИЕ ЛИНИИ НА ЧЕРТЕЖЕ И НАНЕСТИ НА ЧЕРТЁЖ ТОЧКИ, ОБОЗНАЧЕННЫЕ НА НАГЛЯДНОМ ИЗОБРАЖЕНИИ ДЕТАЛИ.
- 18. авесдв1(е1)с1(д1)а1е2в2(с2)а2д2
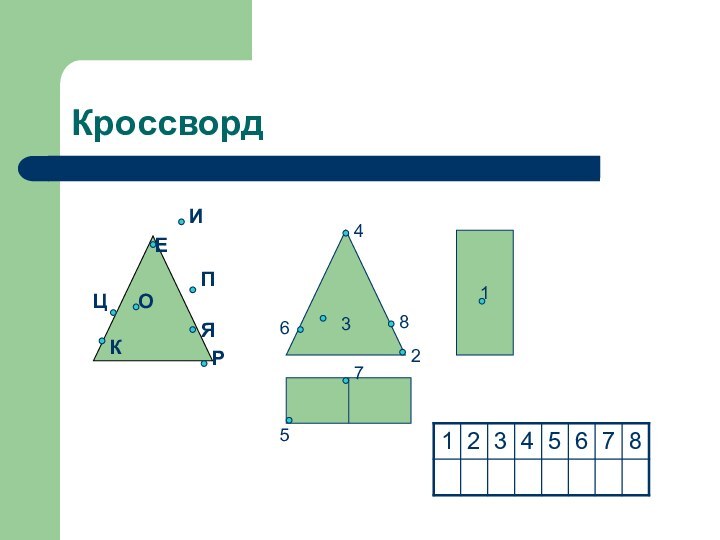
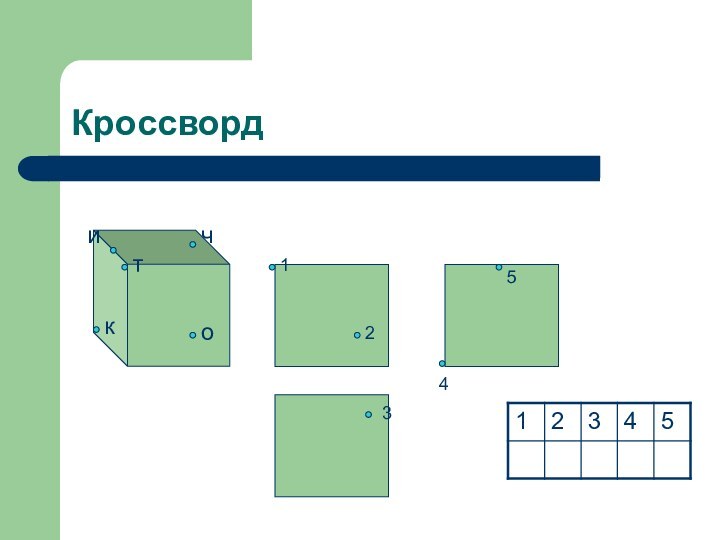
- 19. Кроссворд31ПРОЕКЦИЯ245678
- 20. Кроссвордточки12345
- 21. Задача № 3. Перед Вами чертёж
- 22. Домашнее задание1. Построить чертёж цилиндра размеры которого:Диаметр
- 23. Скачать презентацию
- 24. Похожие презентации
Задание 1: напишите номера видов сверху, которые соответствуют главному виду

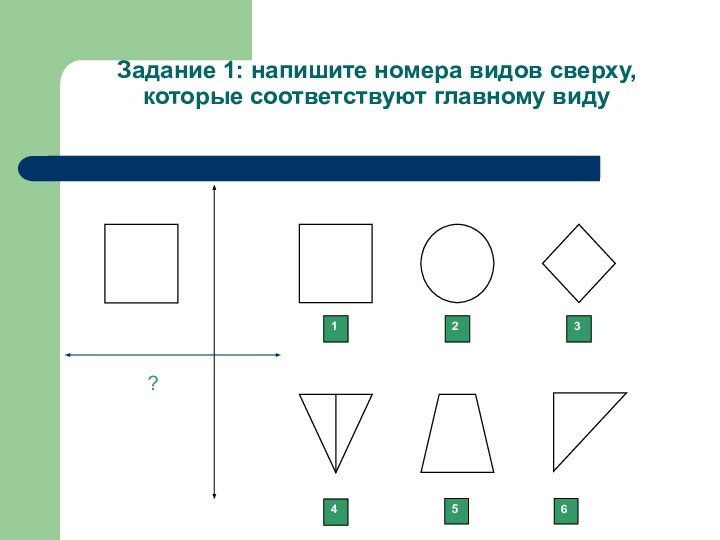








Слайд 4
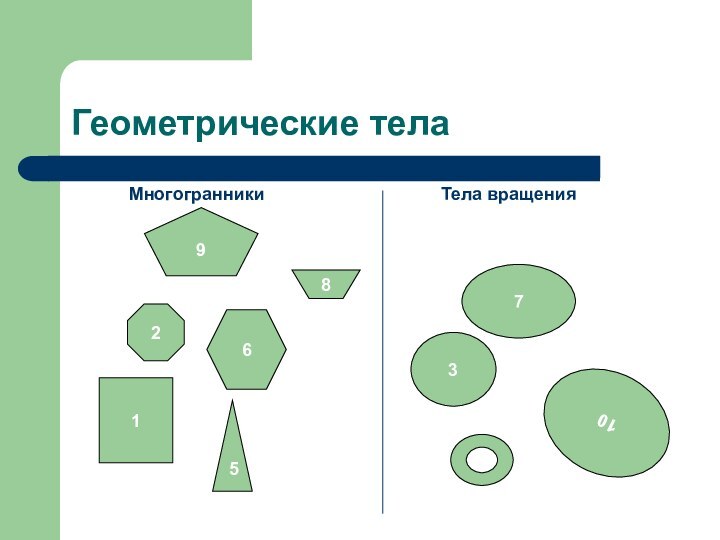
Геометрические тела
10
5
6
7
8
9
2
3
Разделите геометрические тела на многогранники и тела
вращения
1
4
Слайд 6
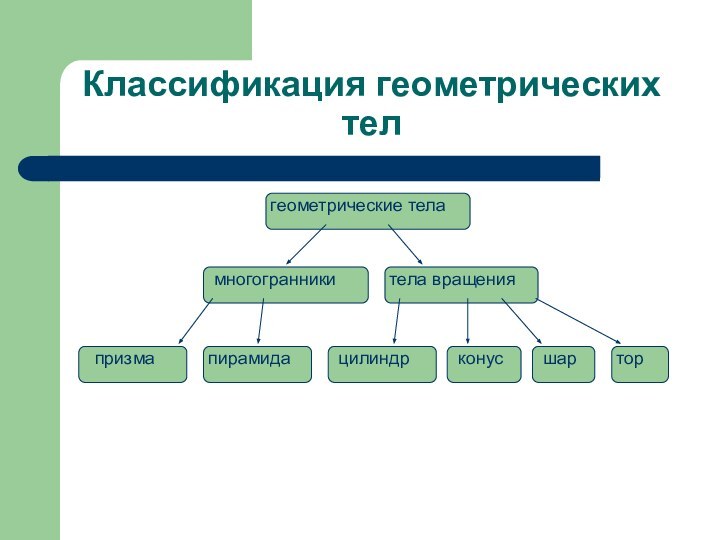
Классификация геометрических тел
геометрические тела
многогранники
тела вращения
призма
пирамида
цилиндр
конус
шар
тор
Слайд 7
Построение проекций точки, лежащей на поверхности предмета
Чтобы
построить проекции точки, заданной на поверхности детали, необходимо понять,
на какой поверхности или на каком элементе поверхности (на ребре, вершине, образующей грани) находится эта точка, а затем уточнить ее геометрическое расположение относительно плоскостей проекций или какого-либо другого элемента формы. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки.
Слайд 8
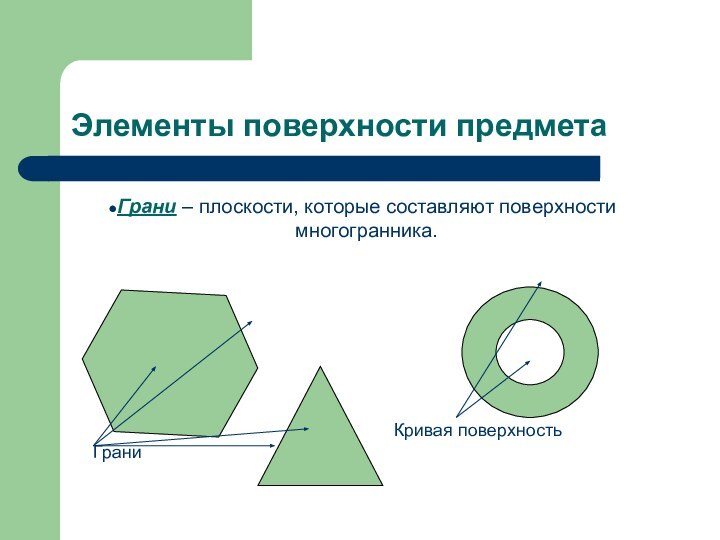
Элементы поверхности предмета
Грани
Кривая поверхность
Грани – плоскости, которые составляют
поверхности многогранника.
Слайд 11
Построение проекций точек
Чтобы задать на чертеже проекции точек,
принадлежащих многограннику или кривой поверхности, необходимо предварительно построить какую-либо
линию на заданной поверхности, а затем на проекциях этой линии взять проекции искомых точек
Слайд 13
На первый взгляд — парадокс: вместо точки строим
линию, чтобы затем найти точку. Тем не менее линию
на поверхности довольно легко построить по двум элементам (например, проведя ее через вершину конуса и точку на основании), а затем найти точку по правилу принадлежности.На рис.87 показано построение точки А, лежащей на поверхности конуса, двумя возможными способами: 1) с помощью образующей 1 = SK; 2) с помощью направляющей окружности.
Слайд 14
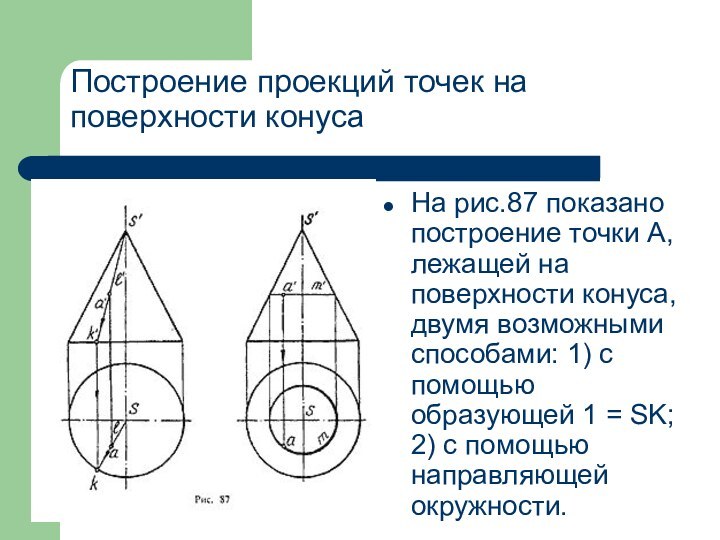
Построение проекций точек на поверхности конуса
На рис.87 показано
построение точки А, лежащей на поверхности конуса, двумя возможными
способами: 1) с помощью образующей 1 = SK; 2) с помощью направляющей окружности.
Слайд 16
Алгоритм построения проекции точки
Анализ геометрической формы предмета по
чертежу
Нахождение проекции видимых точек
Используя метод проекционных связей находим проекции
недостающих точекНаносим условное обозначение проекции точек на видах чертежа
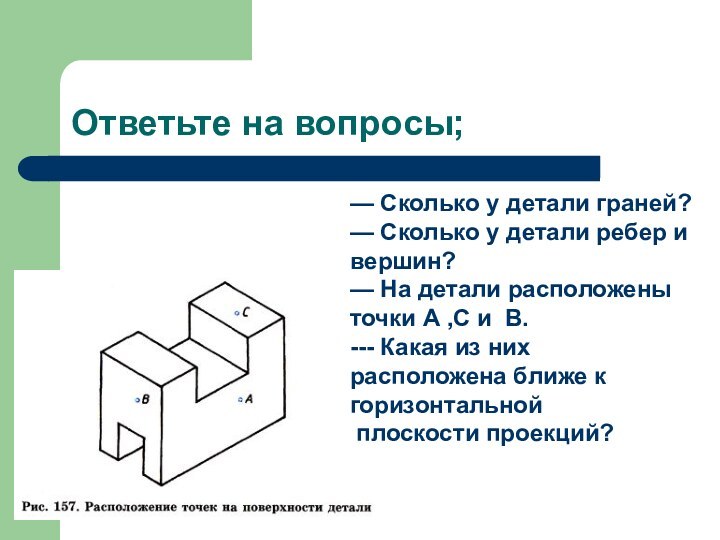
Слайд 17 НАЙТИ НЕДОСТАЮЩИЕ ЛИНИИ НА ЧЕРТЕЖЕ И НАНЕСТИ НА
ЧЕРТЁЖ ТОЧКИ, ОБОЗНАЧЕННЫЕ НА НАГЛЯДНОМ ИЗОБРАЖЕНИИ ДЕТАЛИ.
Слайд 21 Задача № 3. Перед Вами чертёж профилей ботика
XVIII века. На его борту сидит муха. Можем мы
найти её проекцию? Как это лучше сделать?
Слайд 22
Домашнее задание
1. Построить чертёж цилиндра размеры которого:
Диаметр 40
мм, высота 80 мм. Найти три проекции точки. Точка
располагается на кривой поверхности цилиндра на высоте 50 мм от её основания.2. Построить чертёж шара диаметром 60 мм. Нанести на чертёж проекцию любой точки, которая располагается на нём.